【华安金工】低风险组合构建:基于下行风险的缩放策略——“学海拾珠”系列之一百七十二
►主要观点
01
自 Fleming 等人(2001,2003)早期研究以来,波动率缩放方法被广泛应用于市值、贝塔、动量等因子排序投资组合(Barroso and Santa-Clara, 2015; Barroso and Maio, 2016; Cederburg et al., 2020; Daniel and Moskowitz, 2016; Moreira and Muir, 2017)。同时也被应用于股票市场:我们发现,波动率具有持续性,且波动率和股票收益之间的相关性较弱。正是由于波动的持续性特征,未来波动率可以通过滞后波动率来预测,进而导致了滞后波动率和条件夏普比率之间的负相关关系。波动率缩放策略抓住这一特征,在预期条件夏普比率较低时下调风险敞口,在预期条件夏普比率较高时上调风险敞口,以实现最大化风险调整后回报。
本文提出一种风险管理投资策略,其构建方法与波动性缩放类似,只是将波动率替换为能够衡量投资组合下行风险的风险价值(VaR)或条件风险价值(CVaR),我们称之为 VaR 缩放或 CVaR 缩放,若历史数据表明下行风险在未来将上升时,下调投资组合敞口,若下行风险在未来将下降时,上调投资组合敞口。
此种下行风险缩放策略解决了波动性缩放策略的两个问题:下行风险的测量与管理。第一,就风险测量而言,我们知道,若资产回报不符合正态分布,波动率则不能较好衡量真实风险水平。事实上,较早文献(Mandelbrot (1963),Fama (1965))已表明金融资产收益率不符合正态分布(Rachev 等人,2005)。相反,收益率往往表现出负偏和厚尾。这表明,仅通过波动率来衡量会大大低估下行风险,原因在于波动率不能将下行损失和上行收益区分开来,且负偏厚尾分布相比正态分布,其极端损失发生的概率更高。Markowitz (1959)提出使用半方差而不是方差作为风险度量指标,以区分开下行损失和上涨收益。进而,我们选择 VaR 和 CVaR 作为下行风险的度量指标,此种度量也应用于资产配置(Xiong and Idzorek,2011)及银行监管和风险管理(巴塞尔银行监督管理委员会,2010)。
第二,就风险管理而言。在风险缩放策略中引入 VaR 或 CVaR 能够更好管理投资组合的下行风险,从而获得更好的绩效表现。具体地,在刻画下行风险事件时,下行风险测度优于波动率测度,因为在市场下行时刻,使用波动率测度会低估风险,而下行风险测度将为相关投资组合分配更小权重。为进一步探索下行风险测度在管理下行风险方面的表现,我们考虑了 Frazzini 和 Pedersen (2014)的 BAB 策略,即 做多低风险资产,同时做空高风险资产,而且下行风险因子能较好解释资产收益(Schneider 等人,2020)。实证结果表明,与波动性缩放策略相比,下行风险缩放策略的业绩表现更好,能够获得更大的风险调整后回报。
本文的剩余部分组织如下,第 2 节为文献综述,第 3 节将介绍下行风险控制策略的构造,第 4 节将对无缩放策略和波动率缩放策略进行比较,第 5 节为总结。
02
另一方面,有研究对波动率缩放策略的实际投资价值提出质疑,Liu 等(2019)指出,波动率缩放受到前瞻偏差的影响,且若消除前瞻偏差,缩放后的策略为产生比未缩放策略更优的绩效表现。Cederburg 等人(2020)指出 Moreira 和 Muir (2017)中显示的正 alpha 不一定能导致实际可实现的利润。他们通过对大量因子数据集的实证研究,表明除底层策略的选定因子(如 BAB)外,通过波动缩放策略增加的夏普比率在统计上并不显著。
同时,自 Markowitz (1959)和 Roy (1952)以来,基于下行风险的投资研究一直被学者所关注。CVaR 取代了方差和 VaR 等传统风险指标,并被用于解决各种金融风险管理问题(Ban et al., 2018; Lim et al., 2011; Mausser and Romanko, 2018;Xiong and Idzorek, 2011)。Xiong 和 Idzorek (2011)将 CVaR 表示为三阶矩和四阶矩的函数,即在投资组合构建过程中考虑到高阶矩,通过均值-CVaR 优化实现了资产最优配置。实证结果表明,均值-CVaR 优化的投资组合相比均值-方差优化的投资组合具有更好的下行风险特征。Lim 等人(2011)首先研究了抽样误差对数据驱动下的均值-CVaR 优化的投资组合的影响,发现 CVaR 对抽样误差十分敏感。Ban 等人(2018)研究正则化均值-CVaR 优化问题,旨在减少抽样误差和改善优化投资组合的脆弱性。Mausser 和 Romanko (2018)对构建基于 CVaR 的风险平价组合 (Qian, 2005; Maillard et al., 2010)的计算进行了改进。
本文首次提出时序维度上的风险管理投资策略,通过风险缩放策略来分散时序下行风险,而基于 CVaR 的投资策略主要管理截面维度的下跌风险,两种策略都为分散投资决策中的下行风险提供了思路。
03
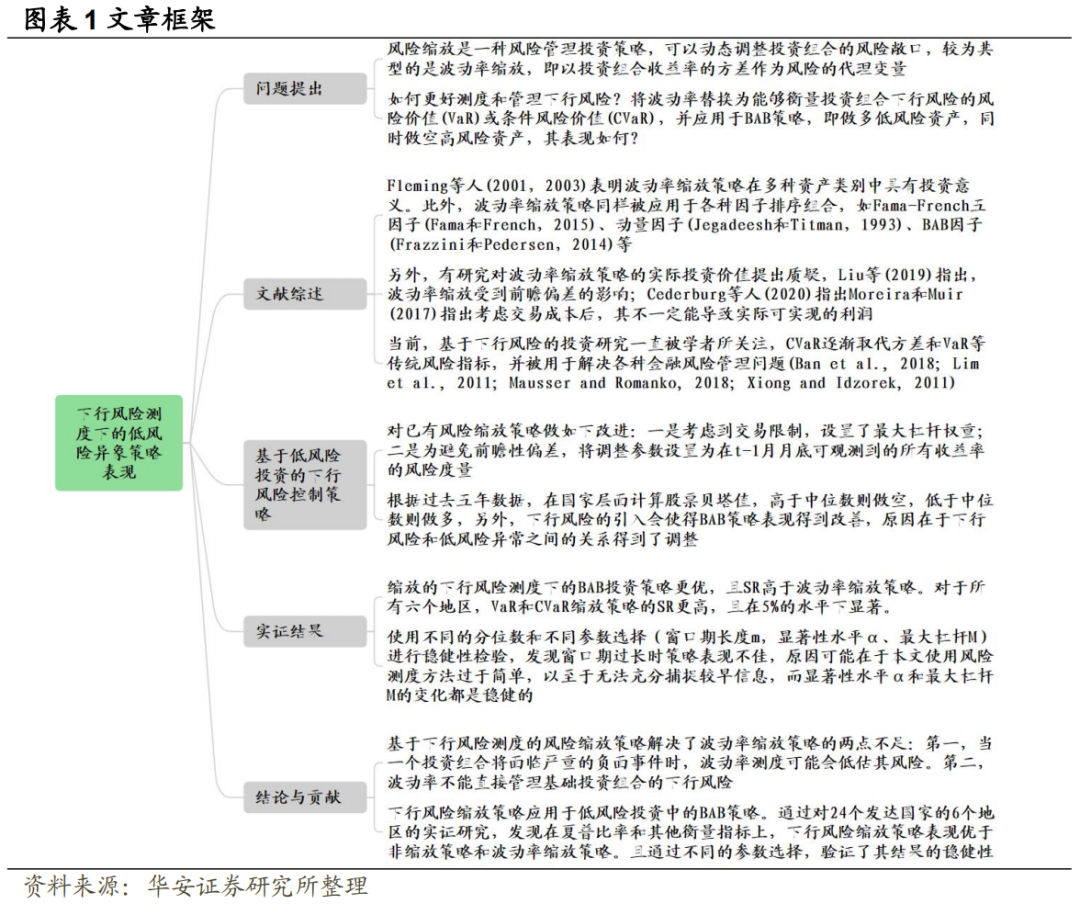
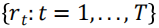 ,将其定义为底层策略。风险缩放是一种动态投资策略,其根据条件风险调整底层策略的权重。应用风险缩放策略,将其收益定义为:
,将其定义为底层策略。风险缩放是一种动态投资策略,其根据条件风险调整底层策略的权重。应用风险缩放策略,将其收益定义为: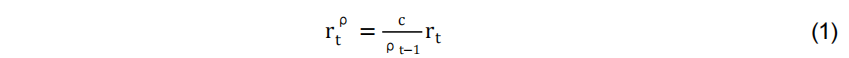
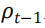 是底层策略在月份t的风险度量,该风险度量是基于截至月份t-1的过去回报预测的,c是一个正的校准参数,用于控制策略的平均敞口。这种风险管理策略在预期进入高风险时期时减少对底层投资组合的敞口,反之亦然。
是底层策略在月份t的风险度量,该风险度量是基于截至月份t-1的过去回报预测的,c是一个正的校准参数,用于控制策略的平均敞口。这种风险管理策略在预期进入高风险时期时减少对底层投资组合的敞口,反之亦然。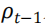 是固定估计窗口下的风险度量,为避免前瞻性偏差,即未缩放和风险缩放回报的无条件波动相等 (Liu et al., 2019; Bongaerts et al., 2020),我们将参数 c 调整为在 t-1 月月底可观测到的所有收益率的风险度量。从而,风险缩放策略调整为:
是固定估计窗口下的风险度量,为避免前瞻性偏差,即未缩放和风险缩放回报的无条件波动相等 (Liu et al., 2019; Bongaerts et al., 2020),我们将参数 c 调整为在 t-1 月月底可观测到的所有收益率的风险度量。从而,风险缩放策略调整为: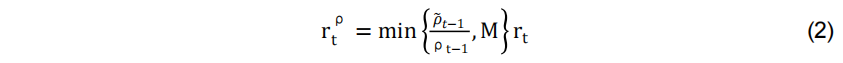
为了在风险缩放策略中使用 VaR 和 CVaR,我们需要预测未缩放时的回报,本文使用了一种最简单的方法,即历史模拟法,其工作原理如下。假设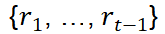 是截至月份 t-1末给出的一系列回报。历史模拟法计算下一个月份t的α-VaR 预测值
是截至月份 t-1末给出的一系列回报。历史模拟法计算下一个月份t的α-VaR 预测值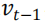 ,作为回报
,作为回报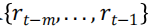 的α-分位数的负值。其中m是估算窗口长度。α-CVaR 预测值
的α-分位数的负值。其中m是估算窗口长度。α-CVaR 预测值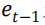 为回报小于或等于
为回报小于或等于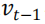 部分的回报的均值。
部分的回报的均值。
BAB 策略是一种多空策略,即买入低贝塔资产,卖出高贝塔资产(Frazzini 和Pedersen,2014)。Moreira 和 Muir (2017)、Cederburg 等人(2020)使用 AQR 数据库中的收益数据构建 BAB 策略,将其考虑进波动率缩放方法。本文通过 BAB 策略构建出包含 24 个 MSCI 发达国家的股票投资组合,数据来源于 CRSP 和XpressFeed 全球数据库。
回归序列构建方法如下。每个月,根据过去五年数据,在国家层面计算超额回报,进而求出该国家股票的贝塔值。通过所有股票贝塔值得出贝塔中位数,高于中位数则做空(将其收益定义为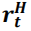 ),低于中位数则做多(将其收益定义为
),低于中位数则做多(将其收益定义为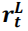 ),由此构建出 BAB 策略。假设多空双方都持有无风险证券(如美国国债,将其收益定义为
),由此构建出 BAB 策略。假设多空双方都持有无风险证券(如美国国债,将其收益定义为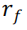 ),BAB 策略回报计算如下:
),BAB 策略回报计算如下:
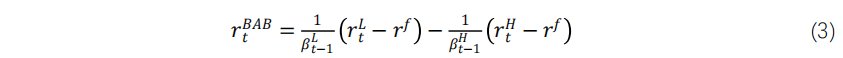
将 BAB 投资组合的多头和空头部分都除以其事前贝塔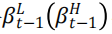 ,以实现对策略的杠杆化或去杠杆化操作,从而将 BAB 策略的事前贝塔值调整为零,使其在市场中保持中性。通过这个操作,投资组合的整体风险将与市场的变动相匹配,而不会受到整体市场的影响。
,以实现对策略的杠杆化或去杠杆化操作,从而将 BAB 策略的事前贝塔值调整为零,使其在市场中保持中性。通过这个操作,投资组合的整体风险将与市场的变动相匹配,而不会受到整体市场的影响。
BAB 策略的盈利源于低贝塔异常,即具有较低(较高)贝塔的股票能获得更多(更少)回报。这意味着,低贝塔股票的α为正,而高贝塔股票的α为负,从而使得BAB 策略的α为正。Alquist 等人(2020)给出了 BAB 盈利能力来源的图解说明。自(Black 等人,1972)以来,低贝塔异常在与各种风险度量下被大家所研究,如特质波动率(Ang 等人,2006),且存在许多利用各种低风险异常的投资策略,统称为低风险投资。本文将 BAB 策略作为低风险投资策略,并遵循最新研究成果(Moreira和 Muir,2017;Cederburg 等人,2020),其中波动性缩放被证明可以提高 BAB策略的风险调整后回报。
我们认为,考虑到下行风险会使得 BAB 策略表现得到改善,原因在于下行风险和低风险异常之间的关系得到了调整。具体来说,Schneider 等人(2020)表明,低风险异常可以用通过协方差刻画的下行风险来解释,协方差定义为:

其中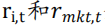 分别是 t 时刻股票 i 和市场的回报率。研究还表明,CAPM 或Fama 和 French (1993)的三因子模型(FF3)下的 BAB 回报残差项与市场回报负相关,这意味着在控制市场或 FF3 因子后,BAB 回报残差项受到市场波动的影响。出于这个原因,若其下行风险得到控制,BAB 策略可能会得到改进。具体而言,当底层策略预计会遭受较大的下行风险时,VaR 或 CVaR 取值会较大,进而下调风险敞口;反之亦然。
分别是 t 时刻股票 i 和市场的回报率。研究还表明,CAPM 或Fama 和 French (1993)的三因子模型(FF3)下的 BAB 回报残差项与市场回报负相关,这意味着在控制市场或 FF3 因子后,BAB 回报残差项受到市场波动的影响。出于这个原因,若其下行风险得到控制,BAB 策略可能会得到改进。具体而言,当底层策略预计会遭受较大的下行风险时,VaR 或 CVaR 取值会较大,进而下调风险敞口;反之亦然。
04
本文实证分析涵盖了 24 个发达国家的 6 个地区的数据。描述性统计见图表 2。平均值、CAPM alpha 和波动率(Vol)都以年化百分比表示,具体地,将平均值和CAPM alpha 乘以 252,将波动率乘以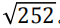 。我们可以看到,BAB 策略在所有六个地区都产生了正回报,且 alpha 在 1%的水平下显著。收益数据显现出负偏(Skew)和尖峰(Kurt ), 由 p-value 可见,Jarque–Bera 检验(jarque 和 bera,1980)拒绝了回报遵循正态分布的假设。BAB 策略回报的这一特征意味着波动率容易低估下行风险,可能不是适当的风险衡量指标。
。我们可以看到,BAB 策略在所有六个地区都产生了正回报,且 alpha 在 1%的水平下显著。收益数据显现出负偏(Skew)和尖峰(Kurt ), 由 p-value 可见,Jarque–Bera 检验(jarque 和 bera,1980)拒绝了回报遵循正态分布的假设。BAB 策略回报的这一特征意味着波动率容易低估下行风险,可能不是适当的风险衡量指标。
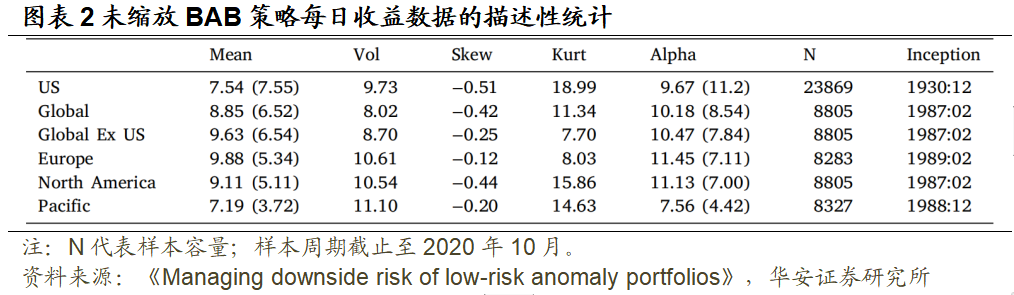
为评估样本外表现,我们采用每月调仓,根据公式(2)重新调整风险敞口,在月初再平衡仓位,并持有到月底。同时,使用 6 个月的窗口期预测风险水平。因此,风险调整策略第一次形成于图表 2 最后一列所示的初始月之后的 6 个月。使用日度收益数据,通过历史模拟法预测随后一期的 5%-VaR 和 5%-CVaR,通过已实现波动率预测随后一期的波动率,乘以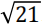 获取月度预测值。具体地,在第 t-1 个月月底,公式(2)的分母
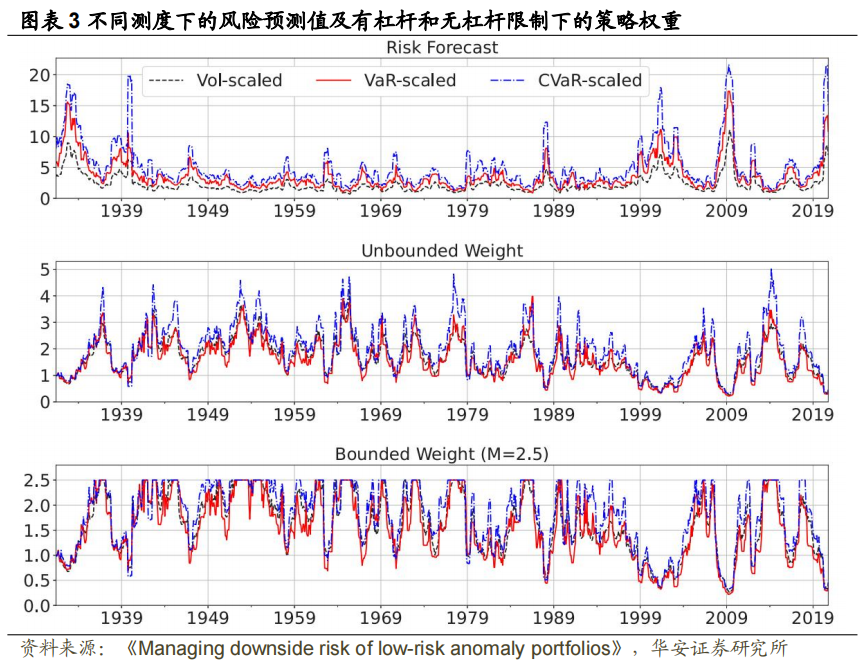
获取月度预测值。具体地,在第 t-1 个月月底,公式(2)的分母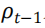 通过第 t-6,...,t-1 月的日度收益数据计算而来,分子
通过第 t-6,...,t-1 月的日度收益数据计算而来,分子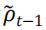 通过第 t 月以前的所有月份的日度数据计算而来。借鉴现有文献(Barroso and Santa-Clara, 2015; Daniel and Moskowitz, 2016; Moreira and Muir, 2017; Cederburg et al., 2020),将最大杠杆 M 设定为 2.5。接着,在第 4.4 节中检验策略稳健性。
通过第 t 月以前的所有月份的日度数据计算而来。借鉴现有文献(Barroso and Santa-Clara, 2015; Daniel and Moskowitz, 2016; Moreira and Muir, 2017; Cederburg et al., 2020),将最大杠杆 M 设定为 2.5。接着,在第 4.4 节中检验策略稳健性。
为进一步说明,根据美国市场未经缩放的 BAB 收益数据,图表 3 中展示了风险预测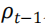 、无杠杆限制下经
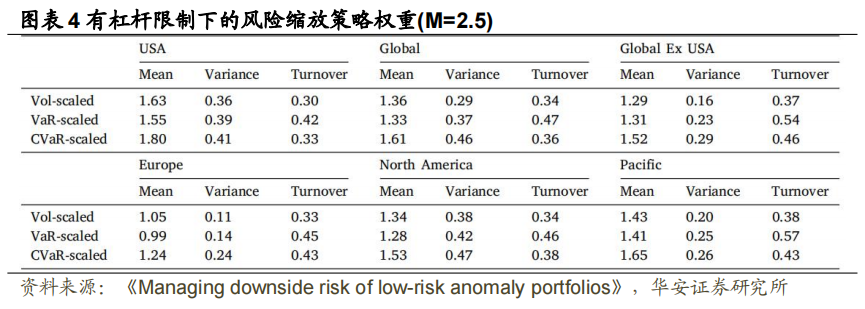
、无杠杆限制下经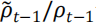 调整后的预测值以及杠杆限制为 2.5 下的预测值。从图中可见,两种下行风险的预测结果总是高于波动率预测,表明 VaR 和CVaR 相比 Vol 更不容易低估风险,同时,也观察到 CVaR 预测总是大于 VaR 预测,符合指标定义,由图可见 CVaR 缩放策略比其他两种缩放策略平均具有更高的权重。图表 4 给出了最大杠杆限制下的描述性统计,并显示 CVaR 缩放策略确实具有更高的平均权重,同时伴随着更高的方差。而波动性和 VaR 缩放策略的平均权重间并无显著大小关系。VaR 缩放策略的最高周转率定义为:
调整后的预测值以及杠杆限制为 2.5 下的预测值。从图中可见,两种下行风险的预测结果总是高于波动率预测,表明 VaR 和CVaR 相比 Vol 更不容易低估风险,同时,也观察到 CVaR 预测总是大于 VaR 预测,符合指标定义,由图可见 CVaR 缩放策略比其他两种缩放策略平均具有更高的权重。图表 4 给出了最大杠杆限制下的描述性统计,并显示 CVaR 缩放策略确实具有更高的平均权重,同时伴随着更高的方差。而波动性和 VaR 缩放策略的平均权重间并无显著大小关系。VaR 缩放策略的最高周转率定义为:
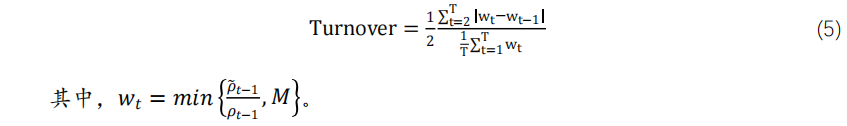
为检验下行风险缩放因子能否对 BAB 策略有贡献,我们进一步探究数据的时序特征。通过 Barroso and Maio (2016)的回归方程检验下行风险因子的可预测性:
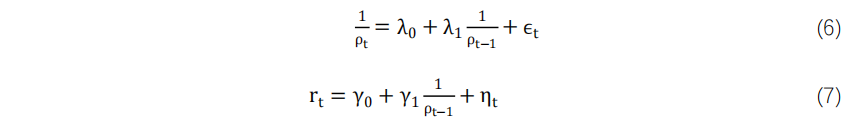
回归方程(6)展示了滞后下行风险的倒数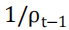 对下一月下行风险
对下一月下行风险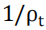 的预测性,回归方程(7)展示了滞后下行风险的倒数
的预测性,回归方程(7)展示了滞后下行风险的倒数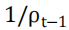 对下一月月度收益
对下一月月度收益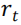 的预测性。由于风险缩放策略采用了倒数处理,根据 Barroso 和 Maio (2016),我们对风险度量的倒数而不是
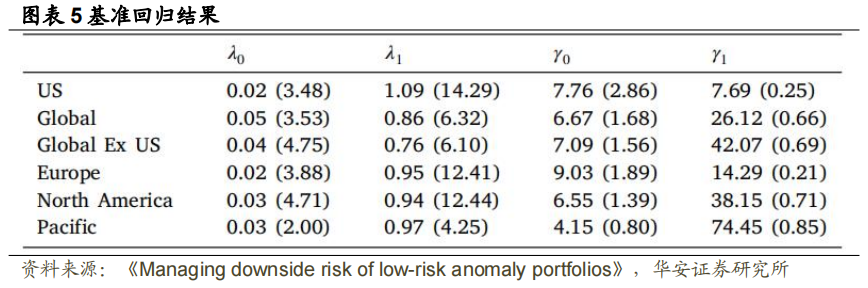
的预测性。由于风险缩放策略采用了倒数处理,根据 Barroso 和 Maio (2016),我们对风险度量的倒数而不是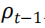 本身进行回归。图表 5 给出了用 CVaR 预测
本身进行回归。图表 5 给出了用 CVaR 预测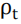 时的回归结果(VaR 的结果同 CVaR 类似)。可见,系数
时的回归结果(VaR 的结果同 CVaR 类似)。可见,系数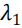 在 1%的水平下显著,表明
在 1%的水平下显著,表明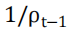 对
对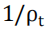 具有预测能力。另外,系数
具有预测能力。另外,系数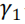 并不显著,表明
并不显著,表明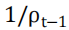 对
对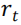 没有预测能力。这一关于未缩放 BAB 策略组合的时序特征表明,当预测下行风险较大(较小)时,投资者可能会从较小(较大)风险权重中获益,原因在于下期的下行风险往往较大(较小),而下期回报在统计上与滞后 CVaR 无关。
没有预测能力。这一关于未缩放 BAB 策略组合的时序特征表明,当预测下行风险较大(较小)时,投资者可能会从较小(较大)风险权重中获益,原因在于下期的下行风险往往较大(较小),而下期回报在统计上与滞后 CVaR 无关。
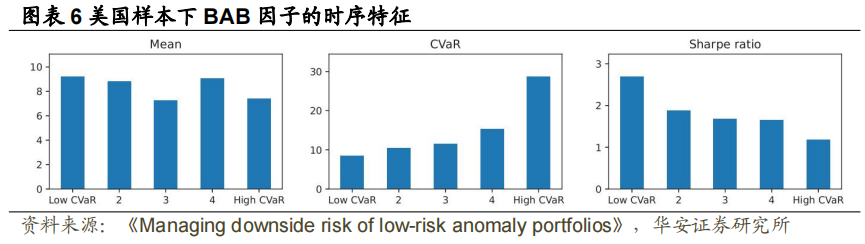
图表 6 进一步展示了上述结论。根据由美国数据样本下的 BAB 日度收益数据计算的 CVaR 分组,分别计算平均回报、CVaR 和夏普比率,图表 6 展示了每组的平均表现。与图表 5 一致,收益率和滞后 CVaR 之间不存在单调性,滞后 CVaR对随后一期的 CVaR 具有较高的预测性,当滞后的 CVaR 较小(较大)时,未缩放的BAB 投资组合的夏普比率较大(较小)。
风险缩放的 BAB 策略表现如图表 7 所示,其中每个面板展示了从图表 2 中给出的开始月份到 2020 年 10 月的整个样本期内每个区域的样本外表现。绩效指标包括均值、Vol、Skew、Kurt、夏普比率(SR)、CVaR 比率(CR) (Xiong 和 Idzorek,2018)、最大回撤(MDD)和 5%-CVaR (CVaR)。SR 定义为平均回报率除以波动率。分子中未减去无风险利率,原因在于 BAB 是自融资策略。CR 定义为平均回报率除以 5%-CVaR,即给定 5%-CVaR 风险水平下的策略回报。均值、波动率、MDD 和CVaR 都为百分比数值。
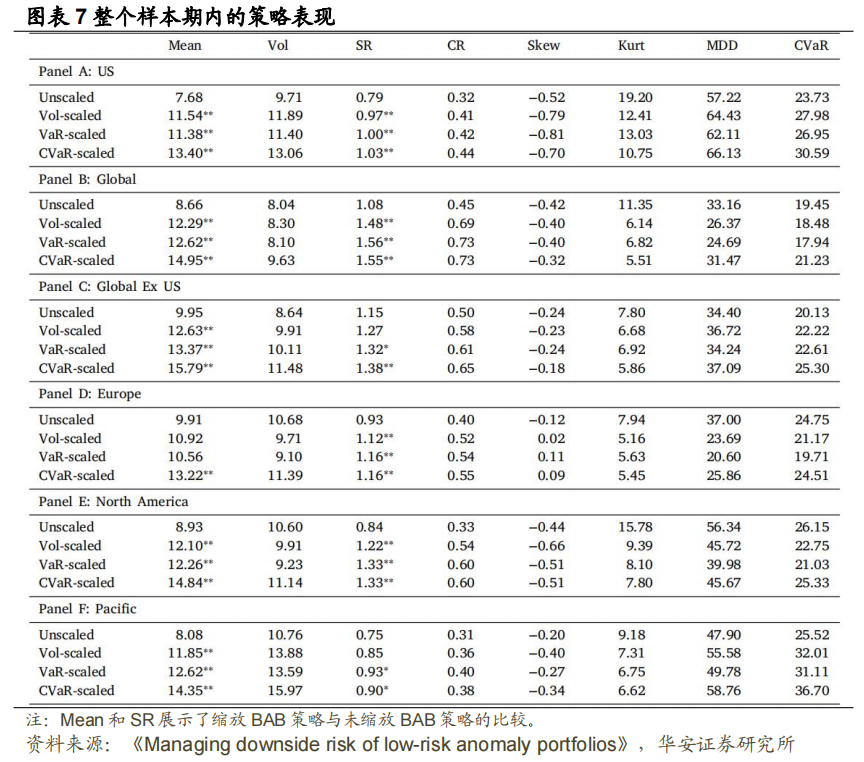
与未缩放的 BAB 策略相比,对风险缩放策略表现在均值和 SR 维度上进行比较。对于均值,我们给出了传统 t 检验对均值收益差异的结果。对于 SR,计算了Ledoit 和 Wolf (2008)统计检验的双边 p 值。在图表 7 中,测试结果由 Mean 和 SR值旁边的星号表示,1 个(2 个)星号表示 5%(1%)的显著性水平。
图表 7 表明缩放的下行风险测度下的 BAB 投资策略更优,且 SR 高于波动率缩放策略。对于所有六个地区,VaR 和 CVaR 缩放策略的 SR 更高,且在 5%的水平下显著。就美国数据而言,VaR 缩放策略的 SR 相比未缩放的 BAB 策略增加了26.6%,CVaR 缩放策略的 SR 相比未缩放的 BAB 增加了 30.4%,而波动率缩放策略的 SR 相比未缩放的 BAB 增加了 22.8%。相比未缩放的 BAB 策略,波动率缩放策略、VaR 缩放策略和 CVaR 缩放策略的平均收益率增幅分别为 24.9%、32.1%和32.8%。将下行风险缩放策略与波动性缩放策略进行比较,我们发现在美国、全球、全球范围初除美国外、北美这四个样本下,CVaR 缩放策略在 1%的水平上有显著改善。在全球和北美这两个样本下,VaR 缩放策略在 5%的水平上有显著改善。
下行风险缩放策略下的 SR 更高,表明风险调整后回报更高,投资者会更加青睐。下行风险缩放策略的较高 SR 也意味着组合了下行风险缩放策略和未缩放或波动比例策略的投资组合会既有较高的风险调整后回报。这是基于这样一个事实,即如果一种策略比另一种策略具有更高的 SR,那么这两种策略的最佳组合在均值-方差意义上比 SR 较小的单一策略会表现更好。但将两种策略的 SR 进行直接比较更为清晰,同时 SR 的增加必然导致以这两种策略为成分的投资组合具有更好的均值-方差表现,且正如 Cederburg 等人(2020)所述,最佳组合不能事先确定,故而文中分析未构建两种策略结合的投资组合,而是直接将两种策略相比较。
图表 7 还列出了其他绩效指标。下行风险缩放策略的峰度更低,但偏度指标未见明显改善。其他与下行风险相关的指标,如 MDD 和 CVaR,与未缩放和波动率缩放的策略相比,CVaR 缩放策略表现更差,原因在于较高的平均权重导致 CVaR缩放策略收益率的波动增加。MDD 和 CVaR 的增加伴随着更高的回报率,进而,基于 CR,我们仍然可认为 CVaR 缩放策略优于未缩放和波动率缩放策略。VaR 缩放策略的样本外波动率与波动率缩放策略相当,尤其可从 MDD 指标中得见。
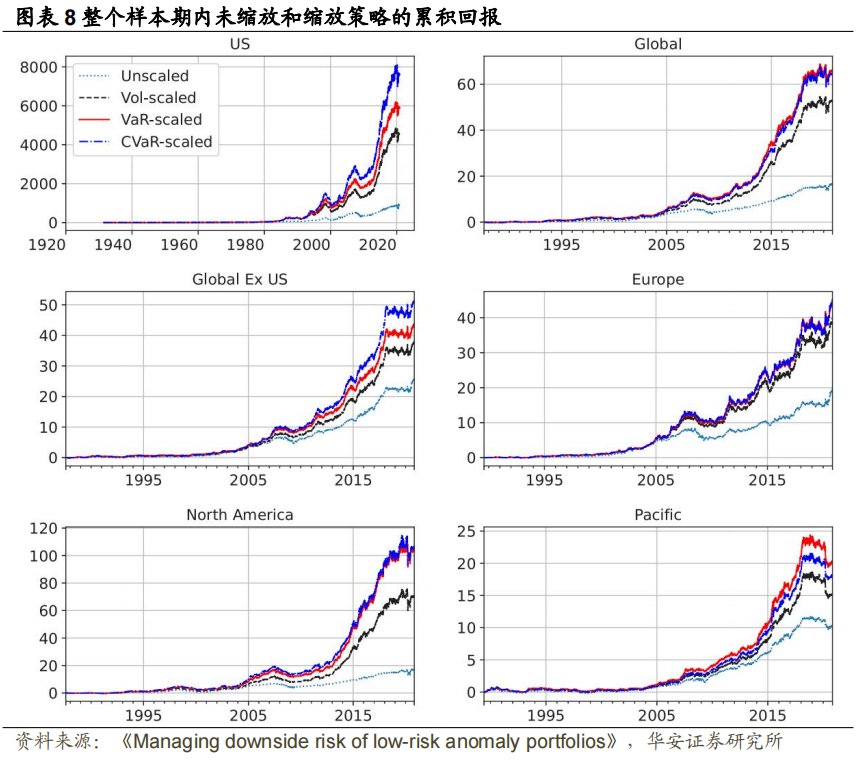
接下来,使用累积回报来展示风险缩放 BAB 策略的样本外表现。由图表 8 可见,下行风险缩放策略的累积回报更高。从长期来看,VaR 缩放策略比未缩放和波动率缩放策略的收益高出至少 1.1 倍,CVaR 缩放策略至少高出 1.4 倍。
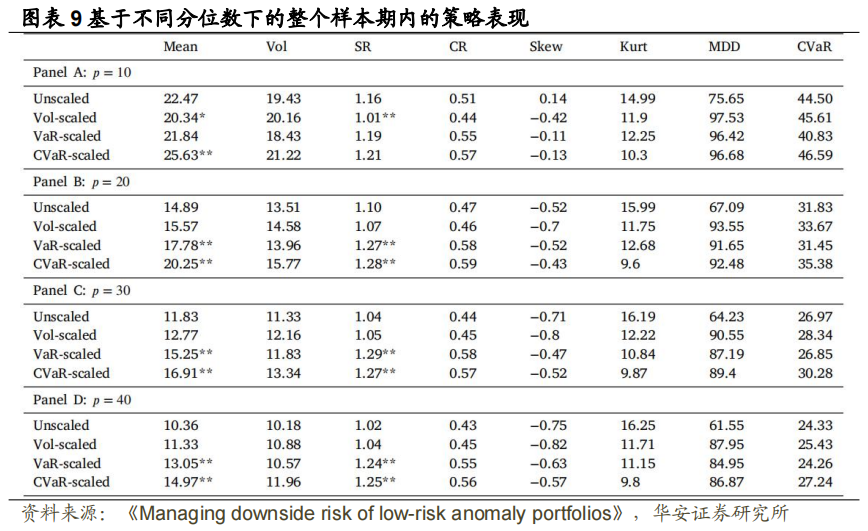
接着,从两个维度对下行风险缩放策略进行稳健性检验。首先,我们讨论了风险缩放策略在应用于不同投资组合时的表现,这些投资组合的构建遵循原始 BAB投资组合的定义,但使用不同的分位数形成多头和空头,而非使用 Frazzini 和Pedersen (2014)中位数切割的方法。我们将 CRSP 数据库中的美国普通股的事前贝塔排序,设置 p ∈ 10,20,30,40 ,做多(空)小于(大于)或等于 p(100-p)百分位贝塔 的股票。样本周期为 1930 年 12 月至 2020 年 10 月,采用每月调仓,可投资股票数量均值为每月 3125 只。
图表 9 显示了与第 4.3 节类似的样本外性能。我们可以看到,除了 p = 10 的情况之外,在 1%的统计显著性方面,下行风险缩放策略表现全面优于未缩放策略和波动率缩放策略。下行风险缩放策略的 CR 较高,收益率和风险测度 Vol、MDD 和CVaR 也随之增加。表明通过下行风险的引入来改善策略表现并不只存在于特定组合中。
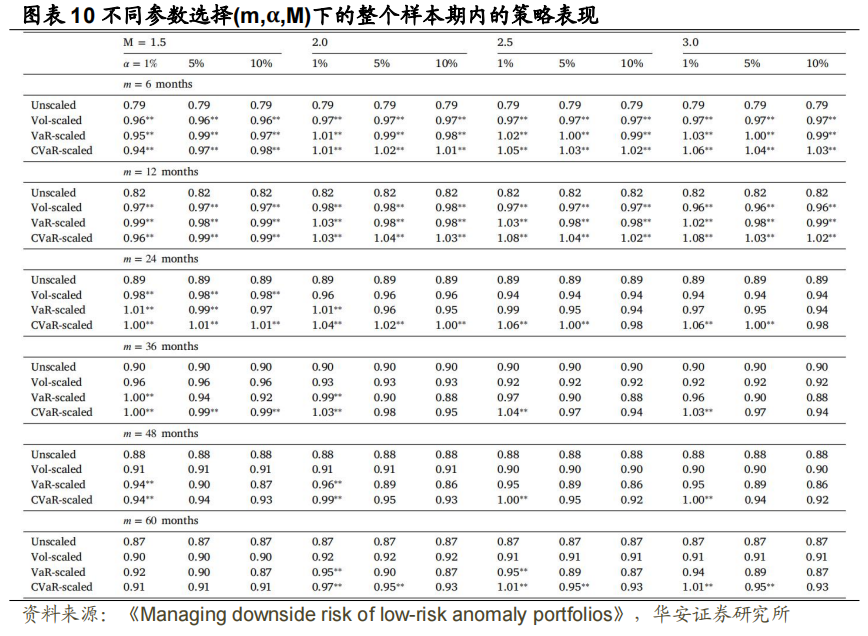
其次,我们使用美国数据探讨了不同参数选择下的策略表现,包括估计窗口长度 m(月数)∈{6,12,24,36,48,60},VaR 和 CVaR 的显著性水平α∈{1%,5%,10%}以及最大杠杆 M∈{1.5,2.0,2.5,3.0}。通过样本外 SR 指标进行比较。
如图表 10 所示,我们可以观察到窗口期长度 m 对三种风险缩放策略性能的影响最大。具体来说,当 m ≥ 24 时,波动率缩放和 VaR 缩放策略表现未明显改善,当 m ≥ 36 时,CVaR 缩放策略表现未明显改善,这表明不应选择过长的窗口期。我们认为,窗口期过长时策略表现不佳,原因在于本文使用风险测度方法过于简单,以至于无法充分捕捉较早信息。另一方面,由下表所示,风险缩放策略的表现对显著性水平α和最大杠杆 M 的变化都是稳健的。
05
本文提出一种基于下行风险测度的风险缩放策略,该策略旨在解决波动率缩放策略的两点不足。第一,当一个投资组合将面临严重的负面事件时,波动率测度可能会低估其风险。第二,波动率不能直接管理基础投资组合的下行风险。进而,我们通过采用风险价值 VaR 和条件风险价值 CVaR 来捕捉和管理基础投资组合的下行风险。
将下行风险缩放策略应用于低风险投资中的 BAB 策略:通过对 24 个发达国家的 6 个地区的实证研究,发现在夏普比率和其他衡量指标上,下行风险缩放策略表现优于非缩放策略和波动率缩放策略。且通过不同的参数选择,验证了其结果的稳健性。
文献来源:
核心内容摘选自Hyuksoo Kim, Saejoon Kim 2021.8.16 发 布 在 Finance Research Letters 的文章《Managing downside risk of low-risk anomaly portfolios》
风险提示
文献结论基于历史数据与海外文献进行总结;不构成任何投资建议。
50.《投资者评价基金时会考虑哪些因素?》
142.《多只新股上市首日涨幅超100%,情绪维持”高温“》
138.《新股市场受资金追捧,打新收益陡升》
122.《科创板新股首日涨幅回暖,首批注册制主板新股迎来上市》
49.《多只新股破发,打新收益曲线调整》
43.《打新账户数量企稳,预计全年2亿A类收益率11.86%》


有态度的金融工程&FOF研究

本篇文章来源于微信公众号: 金工严选