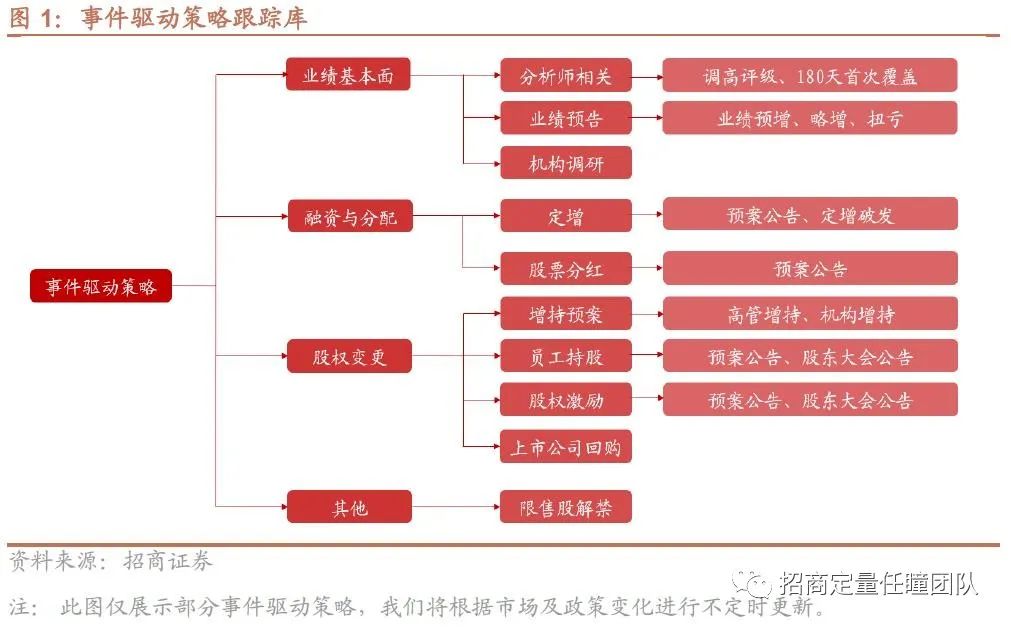
【华安金工】运用少量ETF可以复制主动基金的业绩吗?——“学海拾珠”系列之一百五十
►主要观点
本篇是“学海拾珠”系列第一百五十篇,文献使用交易型开放式指数基金(ETF)作为基准,而不是风险因子,来研究美国主动型共同基金的业绩分布,发现ETF有作为基准进行基金业绩评价的潜力,得出结论:3到5个ETF的组合可以复制大多数主动基金的业绩,也提出了如何选择特定的ETF集合来描述基金业绩,在此方法估计下,有约95%的主动管理基金无法为投资者创造价值。回到国内基金市场,近些年ETF尤其是行业主题ETF规模增长非常迅速,在评估基金业绩时考虑是否能用少量ETF进行业绩复刻可以帮助我们选出真正有能力的主动权益基金。
使用传统的风险因子来描述基金的Alpha对基金而言更具挑战性,因为风险因子中不包含交易成本,而ETF的收益已经包含了交易成本。使用ETF组合,与使用风险因子相比,使用ETF计算得到的基金Alpha较高,两者的差异与投资于风险因子组合所需的交易成本类似。
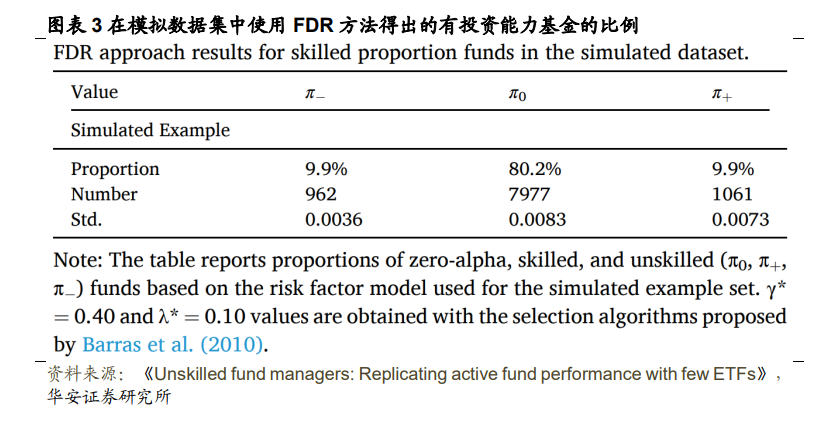
评估基金Alpha的显著性时,即测试基金样本中正Alpha、零Alpha、负Alpha基金的比例时,参考Barras等人(2010)提出的False Discovery Rate(FDR)方法,即调整了零Alpha基金样本中由于运气被统计量错误地识别为正Alpha或负Alpha的基金。
文献结论基于历史数据与海外文献进行总结;不构成任何投资建议。
01
文献使用交易型开放式指数基金(ETF)作为基准,而不是风险因子,来研究主动型共同基金的业绩分布。通过风险因子来描述基金的Alpha对基金而言更具挑战性,因为风险因子中不包含交易成本,而ETF的收益已经包含了交易成本。文献基于Barras、Scaillet和Wermers(2010)提出的False Discovery Rate(FDR)方法,使用2005年至2019年的美国主动基金样本进行评估。
关于Alpha值,本文的结果与使用风险因子得出的结果有所不同,两者之间的差异几乎与投资于风险因子组合所需的交易成本相当(Frazzini、Israel Moskowitz(2012))。另一方面,类似于使用风险因子方法得出的结果(Barras等人(2010)),估计约有95%的美国主动基金无法为其投资者创造价值。此外,随机选择ETF构造组合无法超越主动基金,但是,通过特定方法选择一组ETF可以实现这一目标。
将被动基金作为主动基金的基准并不是一件新鲜事。Malkiel(1995)认为,主动管理者应将被动基金视为机会成本。Sharpe(1992)的使用十二种资产类别指数解释了基金收益。
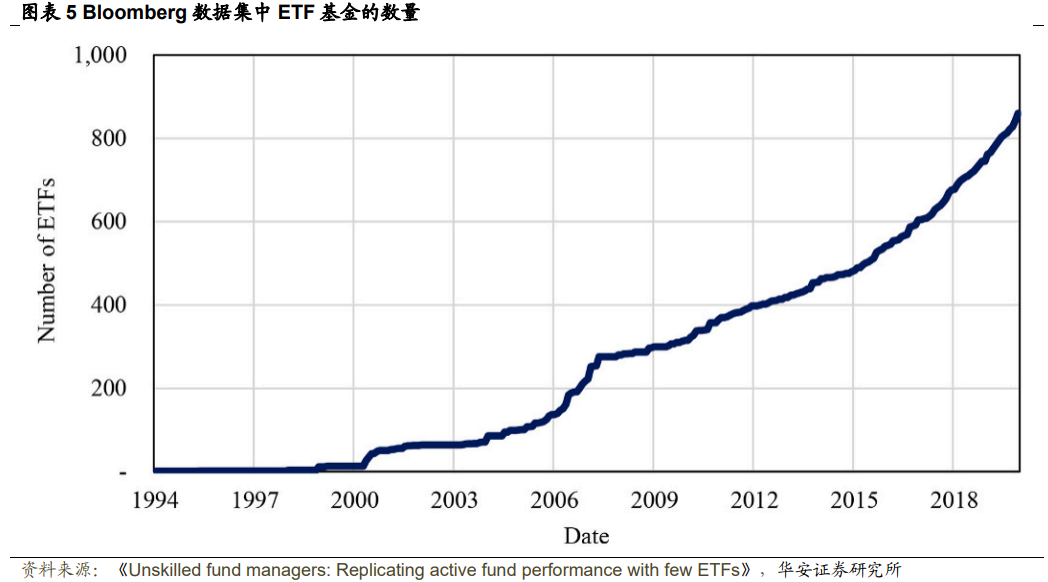
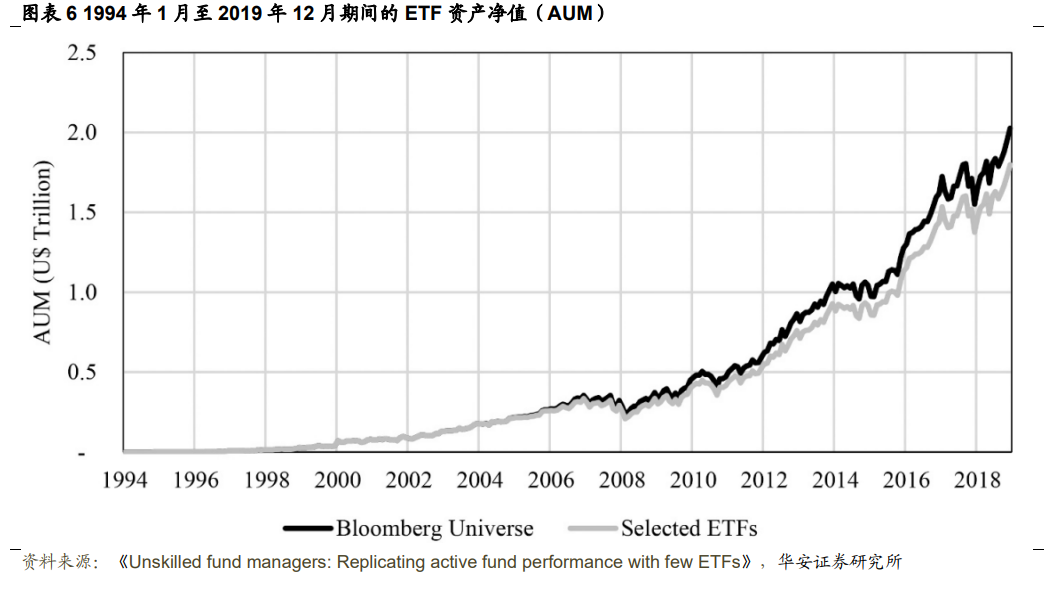
尽管ETF的规模大幅增长,但只有少数研究考虑了它们。运用彭博数据库,筛选了在美国证券交易所上市的2000多只ETF,涵盖了各种资产类别、地理位置和投资策略。若仅考虑美国国内股票市场的ETF,数据集显示有875只基金,截至2019年12月,管理的资产总额达到2.1万亿美元。
为了估计有投资能力的主动基金(skilled active funds)的比例,需要关注特定基金的净收益业绩和成本,从净超额收益中单独计算Alpha值,这通常用于衡量个基的经济收益。因此,在文中,有投资能力的基金被定义为在控制了某些风险之后能够提供异常收益的基金。
从计量经济学的角度来看,评估有投资能力主动基金的比例并非易事,因为必须处理运气成分(假阳性/第一类错误)。已经有许多论文尝试解决这个问题,Fama(2010)提出了一种自助法来计算零Alpha基金的分布,并通过与经验分布进行比较来得出有投资能力基金的分布结论。Pastor和Stambaugh(2002)应用贝叶斯技术,为投资能力匮乏、零Alpha和有投资能力基金的分布设定先验概率。Chen、Cliff和Zhao(2017)假设Alpha基金的分布是参数混合模型。本文采用了Barras等人(2010)提出的False Discovery Rate(FDR)方法。该方法通过计算样本总体中实际幸运基金的比例来控制幸运基金的影响,此外,该方法不需要关于Alpha基金分布的先验假设,并且已经在基金行业研究中广泛应用。
文献提出了特定的算法,使投资者能够选择一组简约的ETF,以评估主动管理基金的业绩。从随机选择一个ETF开始,通过多次重复进行,测试了随机ETF组合在共同基金中的平均超额收益能力。其次,提出了一种基于ETF的超越能力和解释基金收益变动性的能力来选择ETF的算法。最后,通过lasso和正向选择法(forward selection),在风险因子空间中选择ETF。
02
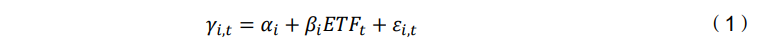
其中𝛾𝑖,𝑡表示第𝑡期的第𝑖只共同基金的超额收益,𝐸𝑇𝐹𝑡是一个(𝑃 × 1)的𝑃个选 定 ETF 基金的超额收益向量,𝑖 ∈ (1, . . . ,𝐼),𝑡 ∈ (1, . . . , 𝑇)。需要强调的是,无论是 共同基金还是ETF基金的收益都是净收益,考虑的是扣除了费用后的投资者直接收 益。
根据模型(1),假设主动管理型共同基金的总体由三个不同的收益类别组成:投资能力匮乏的基金(𝛼 < 0),零Alpha基金(𝛼 = 0)和有投资能力的基金(𝛼 > 0)。因此,如果第 i 只共同基金是一只有投资能力的基金(𝛼𝑖>0),它将产生特异 的正超额收益,并且业绩优于所选的基准。对于任何给定的ETF选择,主要目的是评估样本中有投资能力的共同基金的真 实比例。通过对𝑖 = (1, . . . ,𝐼)进行(1)的估计,直接推断有投资能力的基金比例的 方法是收集来自𝐻0 : 𝛼𝑖 = 0对𝐻1 : 𝛼𝑖 ≠ 0的p值。然而,这种方法未能控制第一类错 误,导致出现了假阳性。这些假阳性被称为幸运基金和不幸基金。为了解决这个问 题,采用 Storey(2002)提出的FDR方法,该方法最初由Barras等人(2010)在 共同基金行业中使用。
为了获得有投资能力基金比例的 FDR 估计,需要确保使用模型(1)估计的个 别检验具有足够的统计功效。因此,本文必须选择一组稀疏的ETF来通过OLS计算(1),并包括足够的时间序列长度,共采用了四种不同类型的ETF选择来获得稀 疏的预测变量集。为了比较不同ETF选择所得到的结果,将以下风险因子模型作为的基准模型:
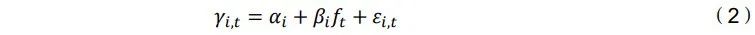
2.1 FDR 方法用于估计有投资能力基金比例
𝐸(𝐹𝛾 +) = 𝜋0通过定义𝜋0为给定显著性水平𝛾下的零 Alpha 基金的比例,𝐹𝛾+的期 望值可以表示为:

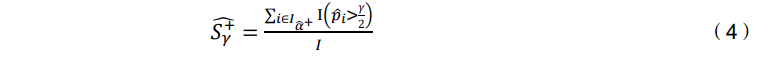
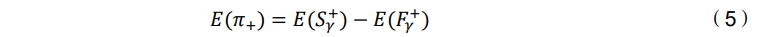
因此,通过对零Alpha基金比例的估计(𝜋̂0),和一个𝛾∗的最优显著性水平, 本文可以计算出𝐸(𝜋+),如下所示:


根据定义和零假设𝐻0 :𝛼𝑖 = 0,对𝐻0 : 𝛼𝑖 = 0 𝑣𝑠 𝐻1 : 𝛼𝑖 ≠ 0进行多重检验会生成 一系列的p值,若基金均为零Alpha基金,则这些p值在[0,1]区间内应该呈现均匀 分布:
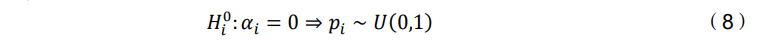
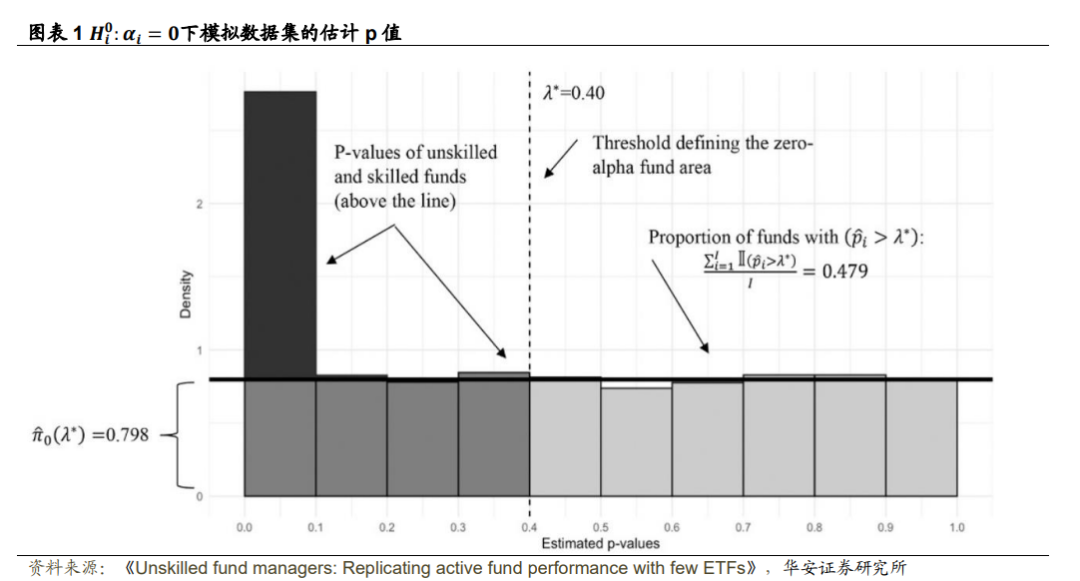
在本文的第二个假设中,假设大于阈值𝜆 ∗的 p 值只能来自零Alpha基金。因此, 考虑到 p 值的经验分布,由∑ Ι(𝑝̂𝑖>𝜆∗)/I 𝑖∈𝐼 给出的区域成为零Alpha基金在[𝜆 ∗ ,1]区间内 的 p 值均匀分布的形状。将该区域扩展至[0,1]范围,可以确定整个均匀分布的比例, 从而计算出𝜋0估计值,即:
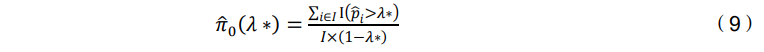
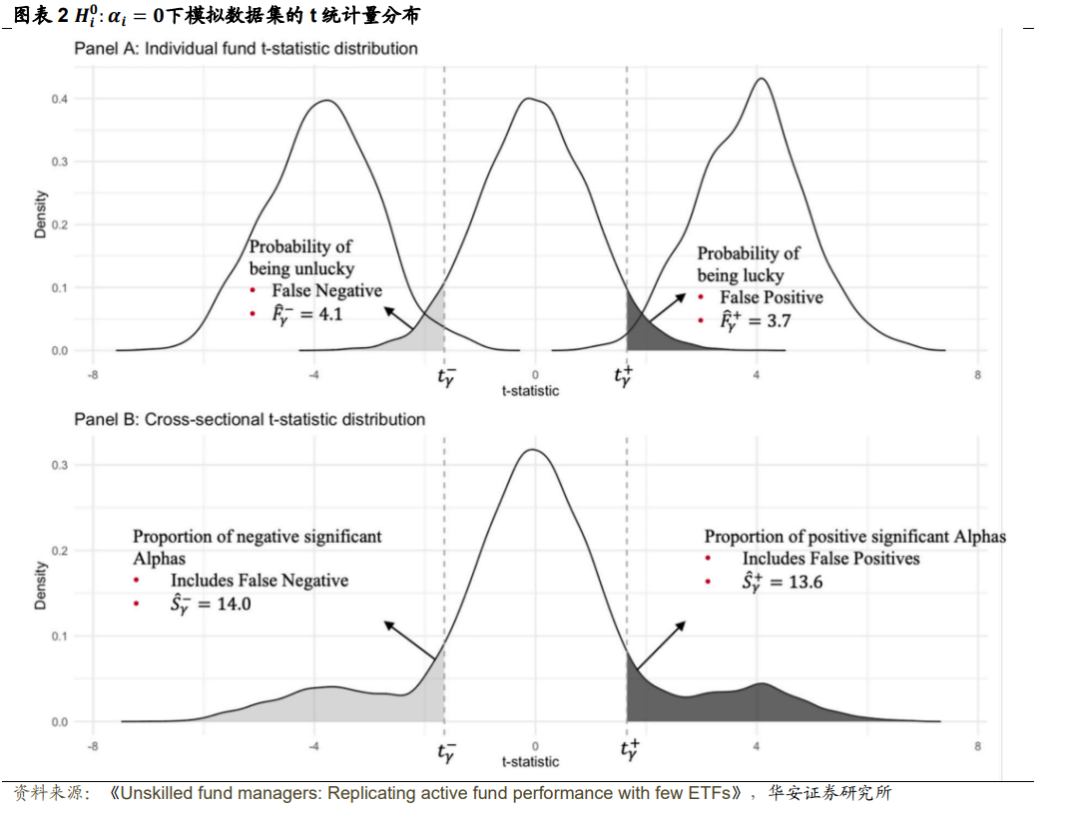
图表2的PanelB显示了与t统计量相关的经验分布。如果本文未能将正显著Alpha由方程(4)描述的𝑆̂𝛾∗+)与假阳性(图表2中面板A的𝐹𝛾∗+区域)进行校正,将得到13.6%的有投资能力的基金比例,而不是最终计算的𝜋̂+的9.9%比例。图表2总结了对模拟数据集的处理结果,可以认为𝜋̂ =(0.106, 0.789, 0.0962)接近原 始参数𝜋=(0.10, 0.80, 0.10)。
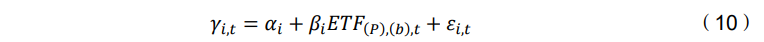
为了测量以下统计量,重复这个过程𝐵 = 500次,因此𝑏 = 1, . . . , 𝐵:
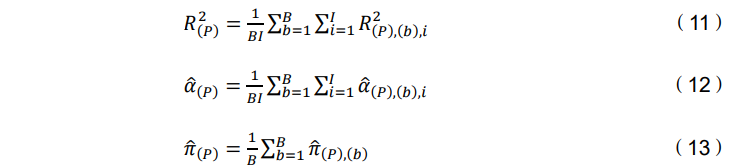
因此,对于选择的𝐸𝑇𝐹𝑡向量维度 P,本文计算所有子样本和所有共同基金中的 平均𝑎𝑑𝑗𝑢𝑠𝑡𝑒𝑑 − 𝑅 2(11),平均计算的 Alpha(12)和平均基金类别比例(13)。
本节描述了一个算法选择,该算法基于ETF的超越共同基金的能力(高𝜋̂+) 和解释基金收益变动性的能力(高平均𝑎𝑑𝑗𝑢𝑠𝑡𝑒𝑑 − 𝑅2)来选择ETF。定义E为原始数据集中可用的 ETFs 的总数 , 因此𝐸𝑇𝐹𝑡= (𝐸𝑇𝐹(1),𝑡 , . . . , 𝐸𝑇𝐹(𝐸),𝑡)。第一步:
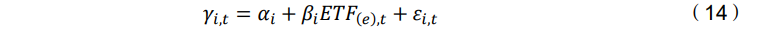
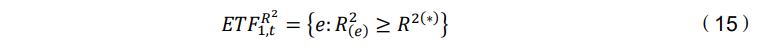
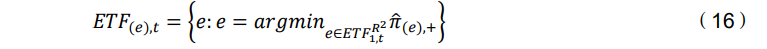
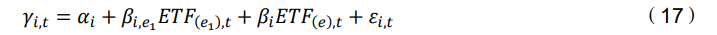
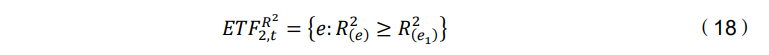 接下来,使用以下方式选择第二个ETF:
接下来,使用以下方式选择第二个ETF: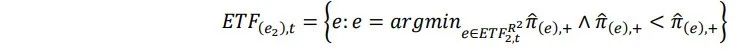
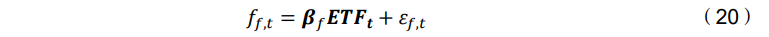
由于原始的 ETF 数据集包含大量的预测变量,为了选择少量的预测变量,因此 将 Lasso 估计器应用于(20),其损失函数如下:
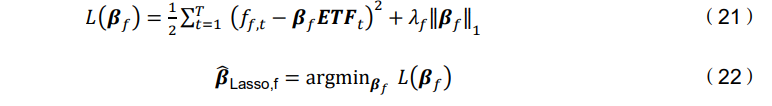
2.5 关于风险因子的正向选择法
03
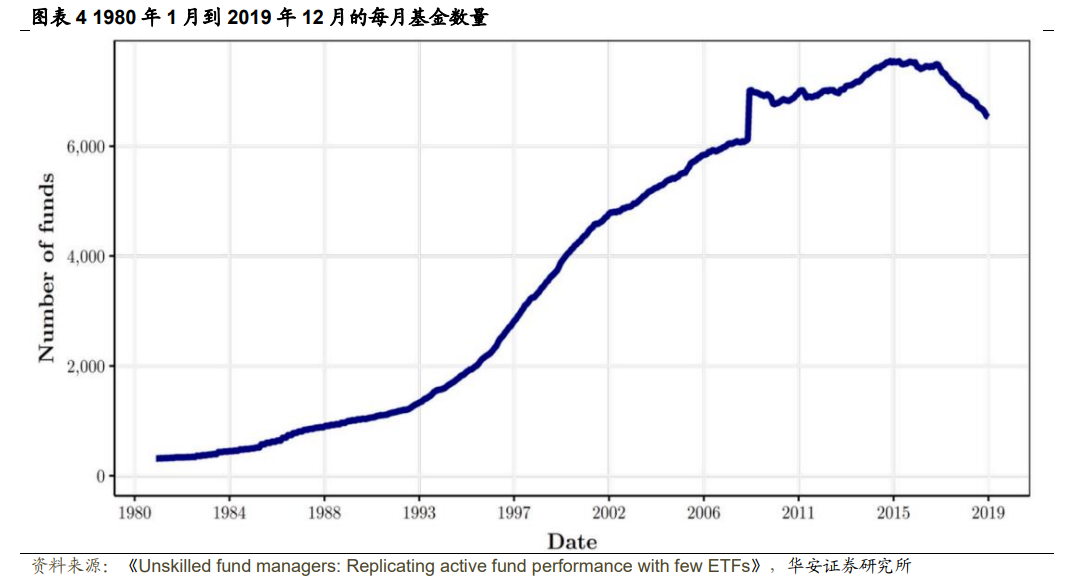
图表41980 年1月到2019 年12月的每月基金数量显示了本文最终数据集中 每个月分析的基金数量。该图清楚地显示出基金数量随着年份的增加而增加的趋势。因此,大多数基金是在近几年观察到的,主要集中在 2005 年1月到2019年12月的范围内。
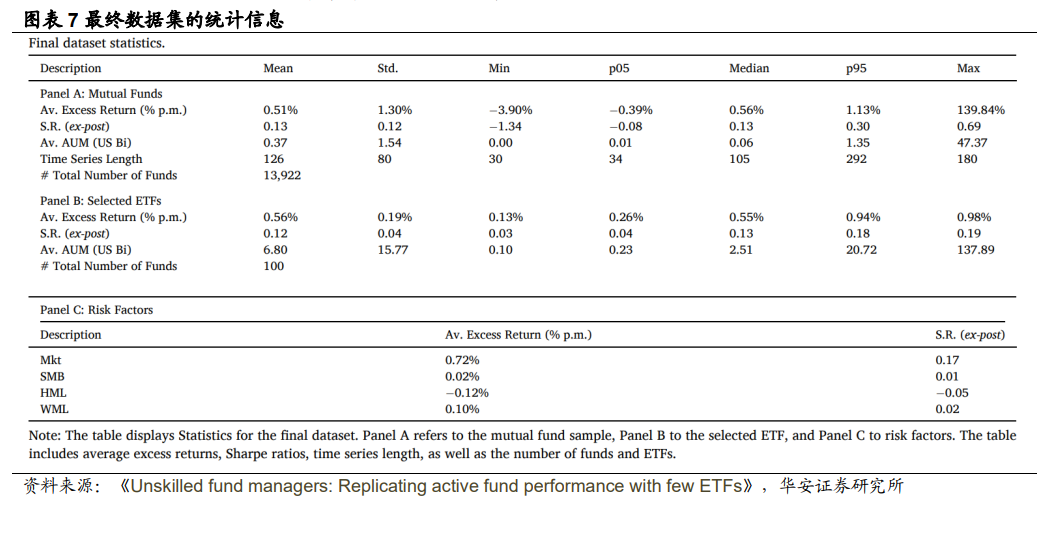
图表 7 最终数据集的统计信息给出了本文的最终数据集(时间跨度为 2005 年1 月至 2019 年 12 月)的统计数据。面板 A 和面板 B 分别汇总了股票型共同基金和 所选 ETF 样本,并进一步详细介绍了平均超额收益、夏普比率、AUM(以十亿美 元计)、时间序列长度以及基金/ETF 的数量。面板C为平均风险因子收益和夏普比 率。
04
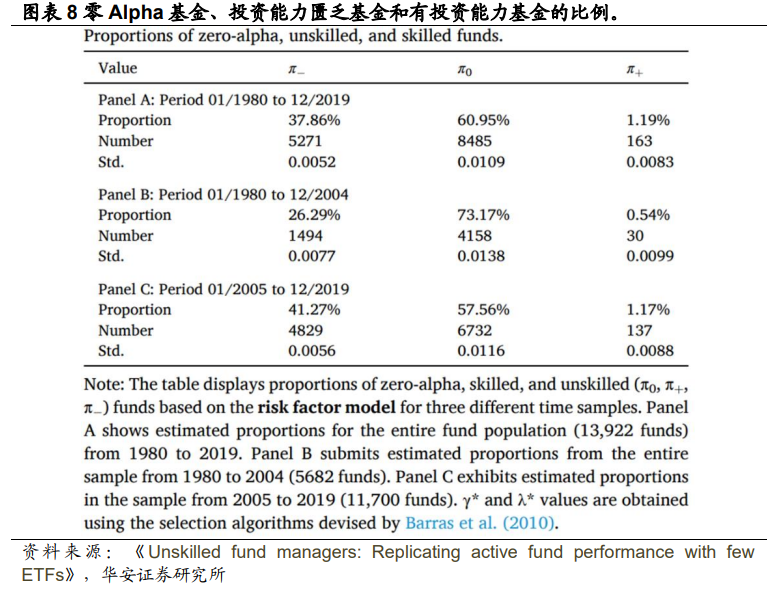
本节展示了ETF在解释基金收益分布方面的潜力。首先应用风险因子模型来评估结果,该模型被用作绩效指标。为此,本文观察了三个子样本中基于投资能力的各种基金比例:第一个子样本涵盖了从1980年到2019年的整个时期;第二个子样本包含了从1980年到2004年的观察数据,这个时间段与Barras等人(2010年)的研究中所考察的时间段相似;最后一个主要时期涵盖了2005年到2019年的年份。
然而,这些结论是通过将基金收益与传统风险因子进行比较得出的,而传统风 险因子是一些在实际投资上存在多个注意事项的理论投资组合。
结果总结在图表 9 随机选择 ETF 与风险因子之间的潜力对比中。上面的面板表 示根据所使用的 ETF 数量的平均 Alpha(超额收益),包含了500个随机组合的测 试,并显示了它们的 95%置信区间。下面的面板则根据考虑的 ETF 数量显示了 𝑎𝑑𝑗𝑢𝑠𝑡𝑒𝑑−𝑅2(解释方差比)。图中的每个点表示平均的500个随机组合,其个别 值是根据2.2节中详细说明的11,700个基金的分布计算得出的。红色虚线代表-0.13%的平均Alpha风险因子和87.7%的平均𝑎𝑑𝑗𝑢𝑠𝑡𝑒𝑑 − 𝑅2。
图表 9 随机选择 ETF 与风险因子之间的潜力对比表明,当考虑大约 6 个 ETF 的组合时,平均 Alpha 会稳定下来。此外,该值稳定在 0.02%的水平,显示它大约 比使用风险因子计算得出的平均 Alpha 高出 0.15%左右。
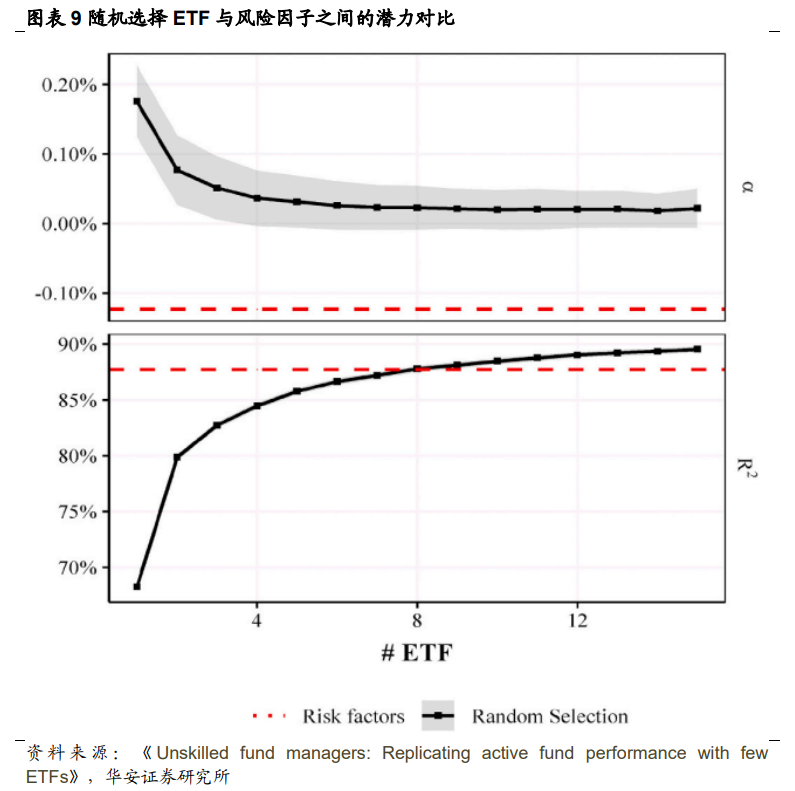
关于𝑎𝑑𝑗𝑢𝑠𝑡𝑒𝑑 − 𝑅2,结果也值得注意,因为当评估包含6个或更多ETF的组 合时,该指标也接近使用风险因子得到的指标。当本文研究包含8个ETF的组合时,𝑎𝑑𝑗𝑢𝑠𝑡𝑒𝑑−𝑅2达到与风险因子相似的平均值(87.7%),而从4个ETF开始, 平均值已经超过了85%。需要大约8个ETF才能获得与4个风险因子相同的𝒂𝒅𝒋𝒖𝒔𝒕𝒆𝒅−𝑹𝟐。
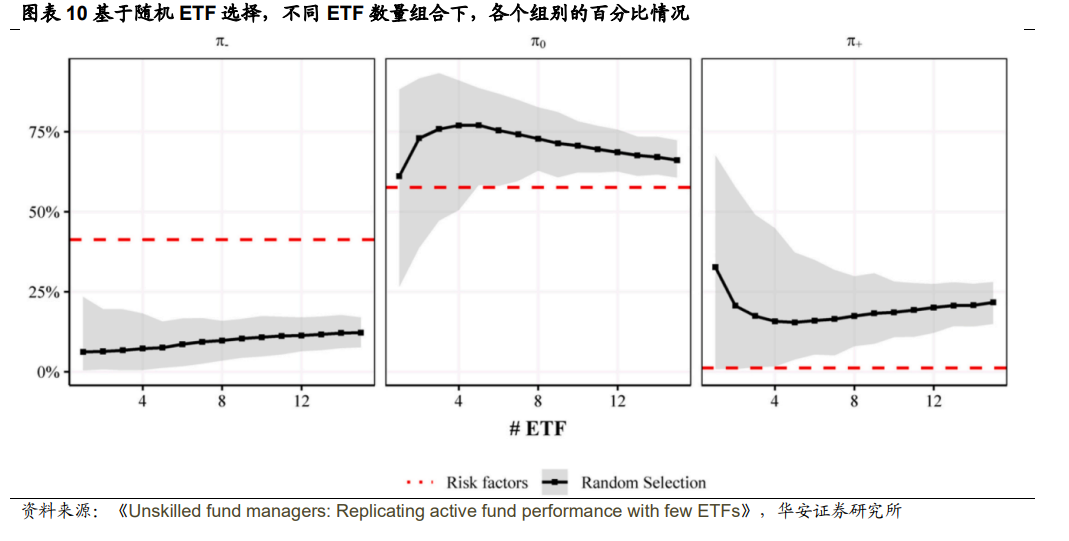
接下来,继续分析图表10,根据在随机组合中评估的 ETF 数量,显示了投资 能力匮乏基金、零 Alpha 基金和有投资能力基金的平均比例。实线黑色线表示分析 的不同ETF数量的随机组合中的平均比例。灰色区域限定了所使用的随机组合的第 2.5 到第97.5 百分位数之间的区间。红色虚线表示根据图表 8 零 Alpha 基金、投资 能力匮乏基金和有投资能力基金的比例,C 面板估计的与风险因子相关的比例:投资能力匮乏基金为41.27%,零Alpha基金为57.56%,有投资能力基金为1.17%。
从投资能力匮乏基金的比例开始,该图支持了图表9随机选择ETF与风险因子 之间的潜力对比中展示的结果。当使用ETF时,投资能力匮乏基金的比例与使用风 险因子时得到的结果不符。将基金收益与ETF组合进行比较时,投资能力匮乏基金 的比例稳定在约10%左右的平均水平,而不受使用的ETF数量的影响。然而,当 考虑风险因子时,这个比例达到了41.27%。这种行为也可以通过风险因子收益中 没有交易成本来解释。没有交易成本,风险因子的平均值可能更高,因此,将这些 变量作为基准可能会产生更低的Alpha (超额收益),以及更高的投资能力匮乏基 金比例。这种模式与图表9随机选择ETF与风险因子之间的潜力对比中的结论一 致,当将ETF作为参考时,平均Alpha较高。
相比之下,虽然投资能力匮乏基金的比例是稳定的,但零 Alpha 基金和有投资 能力基金的比例似乎对所分析的 ETF 数量敏感,并呈完全相反的方式变化。随着本 文研究越来越多的 ETF 组合,计算得出的零 Alpha 基金比例上升,而估计的有投 资能力基金比例下降。实际上,本文预期会发生相反的情况,因为这三个比例相加 等于100%,而投资能力匮乏基金的比例保持稳定。然而,当本文考虑百分位数从2.5%到97.5%的区间时,注意到产生与风险因子相似结果的 ETF 组合确实存在, 因为灰色区域与代表风险因子的红色虚线相交。此外,就平均比例而言,可以明确 看出,为了解释基金的绩效,使用3到5个 ETF 组合所获得的最佳结果,因为零 Alpha 基金比例在这个区间达到了顶峰,而有投资能力基金的比例降至最低点。
图表 10 中显示的另一种模式涉及到有投资能力基金比例的正向趋势,这可能 表明随着继续测试增加 ETF 数量,有投资能力基金的比例也会上升。起初,这种模 式可能看起来不寻常,然而,必须记住 ETF 是随机选择的,因此,随着开始考虑更 多的 ETF 组合,可能性的数量迅速增加,因此很难只通过增加特定的 ETF 来再次 评估相同的组合。
本节得出以下结论:(i)ETF可以用作评估基金绩效的基准;(ii)应该只比较有投 资能力基金的比例,因为交易成本表明使用风险因子和 ETF 所获得的投资能力匮 乏基金比例存在差异;(iii)最佳的 ETF 组合不应偏离 3 到 5 个 ETF 的范围太远。
根据第4.1节的结果,采用以下专门的方法来确定最佳的 ETF 组合。与前一节 不同,本节通过特定的方式选择组合。一共有两个方法。第一个方法在第4.2.1节中详细介绍,它选择了一组 ETF, 旨在复制有投资能力基金比例、𝑎𝑑𝑗𝑢𝑠𝑡𝑒𝑑−𝑅2和 Alpha(超额收益)方面的最佳结 果。第二种方法使用一个模型来识别一组复制风险因子维度的ETF。这两种方法的 目的相同:选择最佳的基准用于基金样本。然而,第一个方法通过基金收益维度来 解决这个问题,而第二个方法则从风险因子的角度进行处理。
本节研究在基金维度选择ETF的结果。该方法旨在:(1)确定能够解释基金 收益变化性(高𝑎𝑑𝑗𝑢𝑠𝑡𝑒𝑑−𝑅2)的ETF组合;(2)生成较低比例的有投资能力基 金(低𝜋+);以及推荐具有较低风险调整超额收益的平均值(低 Alpha)。
如第 2.3 节所述,使用的流程是依次选择ETF,即每次迭代中选择一个ETF, 从而生成平均𝑎𝑑𝑗𝑢𝑠𝑡𝑒𝑑−𝑅2大于85%的最低比例的有投资能力基金,并且高于使 用最后选择的 ETF 获得的𝑎𝑑𝑗𝑢𝑠𝑡𝑒𝑑 −𝑅2 . 因此,第一个ETF的选择是为了尽量减 少有投资能力基金的比例,并且满足平均𝑎𝑑𝑗𝑢𝑠𝑡𝑒𝑑−𝑅2 ≥ 85%的条件。然后继续 添加其他的 ETF,始终最小化有投资能力基金的比例,并且只考虑那些生成的平均 𝑎𝑑𝑗𝑢𝑠𝑡𝑒𝑑 − 𝑅2大于或等于上一次迭代中获得的值的选项。当本文确定额外的ETF无法降低估计的有投资能力基金比例时,流程结束。
设定最低𝑎𝑑𝑗𝑢𝑠𝑡𝑒𝑑−𝑅2有助于避免回归结果对数据的弱拟合,并减少有投资 能力基金和投资能力匮乏基金的 p 值计算的潜在分布的波动。
在应用上述流程后,选择了五个 ETF:VV⋅U、IJT、SLYV、XLY 和 XLV。在 评估基于这些 ETF 的有投资能力基金比例之前,分析是否能够涵盖每个风险因子。为了做到这一点,对于每个风险因子,对 ETF 组合上进行时间序列回归,并评估截 距的显著性。
可以在图表11基于基金业绩分布的ETF选择结果中找到这个选择中使用的绩 效指标分布结果(结合四个基准 ETF)以及投资能力匮乏基金、零 Alpha 基金和有 投资能力基金的估计比例。面板A显示了业绩分布指标,而面板B显示了有投资能 力的比例。
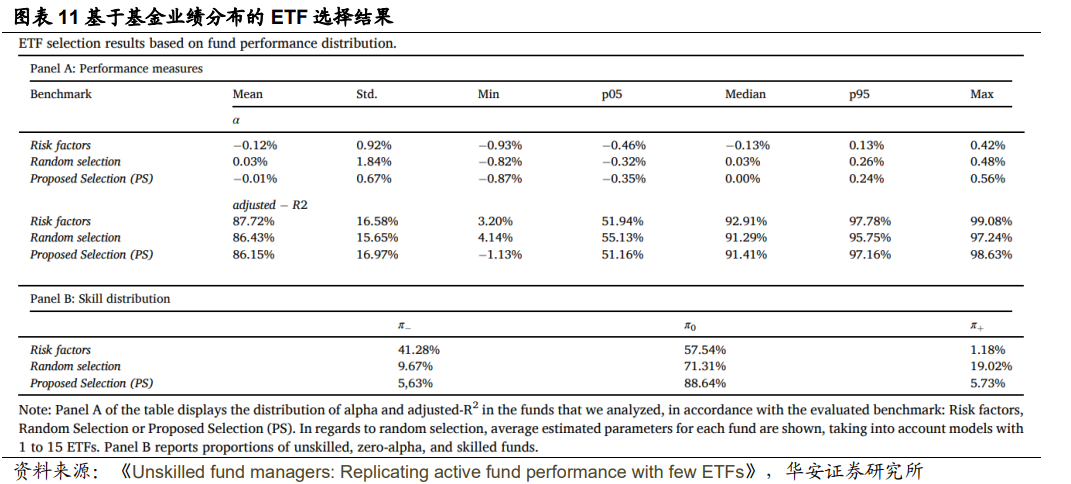
从所分析的每个指标来看,这些结果超过了简单地随机选择ETF所获得的结果。此外,它们与风险因子获得的值接近,除了平均Alpha,尽管它是负值,但仍然比 估计的风险因子高约0.11%。
最后,正如所看到的,估计的有投资能力基金比例仅为5.73%。因此,基于所 选的ETF组合,估计94.27%的基金都没有正向风险调整收益。这个结果再次佐证 过往研究中的证据,即使考虑到所有交易成本,这一结果仍然成立。通过分析基金 的总收益(即扣除费用之前的收益),可以得到类似的结果。
本节采用特定的方法来选择一组能够模拟风险因子收益的ETF。目标是尝试找 到一组 ETF,可以在将基金收益暴露给风险因子时复制结果。第一个测试的方法基于Lasso方法,并将一组ETF视为风险因子的潜在解释变 量。对每个风险因子应用Lasso方法,以确定能够解释风险因子变动性的ETF组 合。每个风险因子的所选ETF在图表12中列出。表格的最后一行报告了通过所选ETF对风险因子进行回归后得到的𝑎𝑑𝑗𝑢𝑠𝑡𝑒𝑑 − 𝑅2。
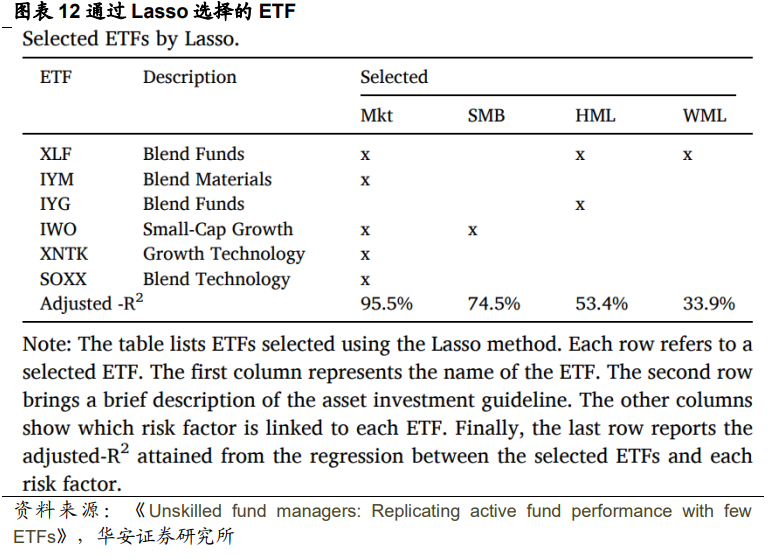
该方法选择了五个 ETF 来解释市场风险因子的变动性,但其中两个 ETF 也被 用于解释 HML、WML 和 SMB 因子。HML 因子需要选择两个ETF。最后,SMB 和 WML要求选择额外的一个ETF。总共选择了六个ETF,𝑎𝑑𝑗𝑢𝑠𝑡𝑒𝑑−𝑅2的范围为95.5%到33.9%。第二个选择的方法是基于正向选择方法。具体而言,该方法包括每个风险因子 选择的一组ETF,以获得尽可能高的𝑎𝑑𝑗𝑢𝑠𝑡𝑒𝑑−𝑅2。该方法在每次迭代中为每个 风险因子选择一个 ETF。除非选择相同的ETF来解释不同的风险因子,否则在每次 新的迭代中选择四个 ETF 的集合。只评估了每个风险因子最多选择 2 个ETF的结果。所选的 ETF 在图表13通过 正向选择选择的 ETF 中显示,其中Forward 1和Forward 2分别表示选择每个风险 因子一个到两个ETF时得到的结果。
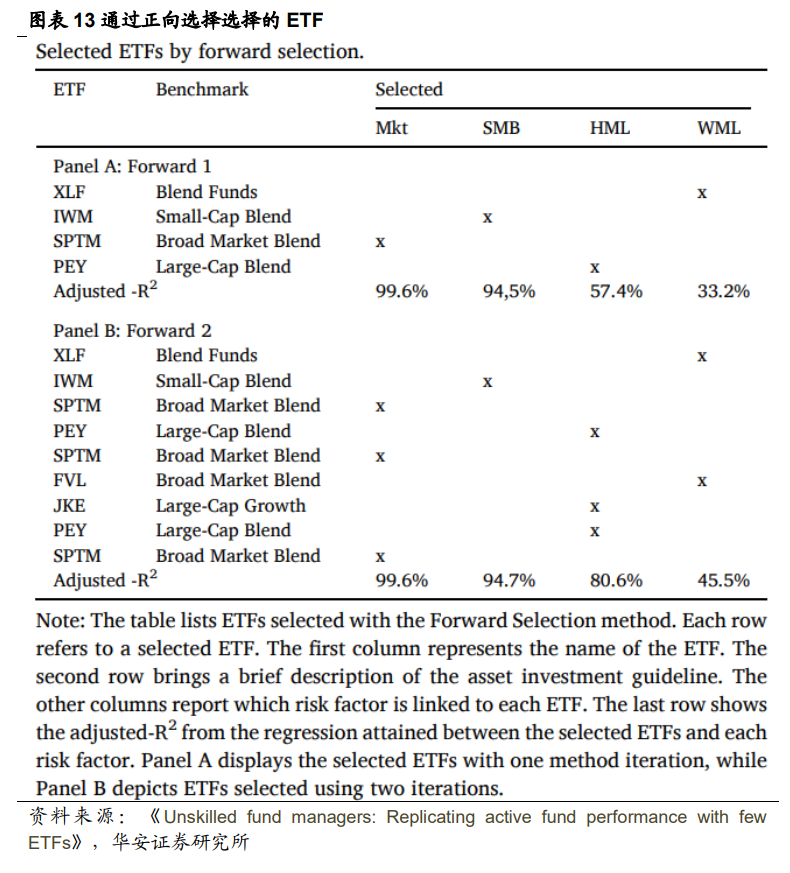
结果显示,每个风险因子选择的 ETF 不相交,因此在第一次迭代中选择了总共 四个 ETF(Forward 1),在第二次迭代中选择了额外的四个ETF(Forward 2)。当选择一个 ETF 时,𝑎𝑑𝑗𝑢𝑠𝑡𝑒𝑑 − 𝑅2的范围为 99.6%到 33.2%,当选择两个ETF时,𝑎𝑑𝑗𝑢𝑠𝑡𝑒𝑑−𝑅2的范围为 99.6%到 45.5%。
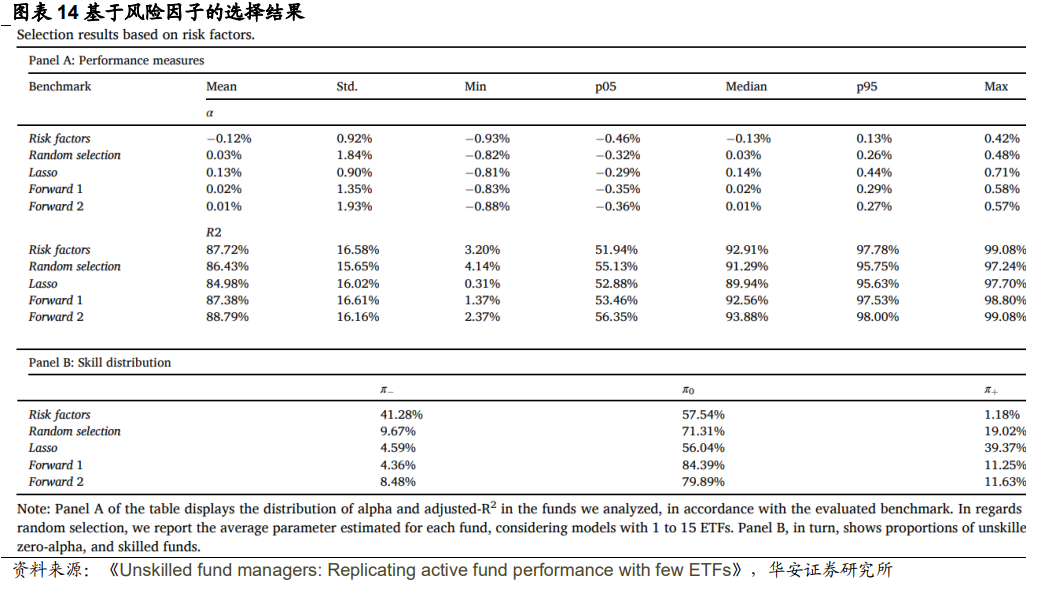
所采用的方法表明选择的ETF能够解释主动管理投资基金的收益变得越来越可 能。然而,尽管这些结果超过了随机选择ETF的结果,但估计的有投资能力基金比 例仍然显著高于使用风险因子估计的比例。值得注意的是,这些方法并不受潜在数 据浏览的影响,因为本文在这里通过分析风险因子维度选择ETF,而不是直接从基 金中选择。
05
近年来,ETF的数量大幅增长。本文通过研究这一事实,旨在更好地理解与主 动基金业绩相关的投资能力分布。在ETF市场中,许多ETF组合适合用作评估主 动管理基金的基准。关于有投资能力基金经理比例的估计,本文得出的结果与传统 风险因子的估计相似。然而,与风险因子相比,实际上在市场上交易ETF更适合这 项任务,因为它们是合法可投资的金融工具。
在分析随机选择的ETF组合之后,本文可以得出以下结论:(i)ETF可以用作 评估基金业绩的基准;(ii)本文只应比较有投资能力基金的比例,因为交易成本表 明使用风险因子和ETF获得的投资能力匮乏基金比例存在差异;(iii)最佳的ETF组 合应在3到5个ETF的范围内。
然而,本文还发现,不同的ETF组合导致了在主动基金群体中观察到的行为差异。因此,这证明了需要一种引导性的方法来选择具备评估基金所需特征的ETF。
在这种背景下,本文进行了一系列选择算法的测试,发现可以找到合适的组合。本文还研究了基于交叉验证的算法性能,发现根据评估的大约5个ETF的组合,约95%的主动共同基金行业既没有必要的投资能力,也没有为其投资者创造价值的能 力。
核心内容摘选自 Fernando Moraes, Elias Cavalcante-Filho, Rodrigo De-Losso 在《International Review of Financial Analysis》的文章《Unskilled fund managers: Replicating active fund performance with few ETFs》
风险提示
文献结论基于历史数据与海外文献进行总结;不构成任何投资建议。
148.《投资者情绪能预测规模溢价吗》
50.《投资者评价基金时会考虑哪些因素?》
122.《科创板新股首日涨幅回暖,首批注册制主板新股迎来上市》
49.《多只新股破发,打新收益曲线调整》
43.《打新账户数量企稳,预计全年2亿A类收益率11.86%》


有态度的金融工程&FOF研究

本篇文章来源于微信公众号: 金工严选