【浙商金工】主动基金究竟能否创造alpha收益?


摘要

01
选题背景
面对主动基金较弱的alpha收益,指数基金的强势是美国投资者“用脚投票”的结果。2013年至2022年,美国股票型指数基金(含ETF在内)累计吸引了2.5万亿美元的净新资金流入,而同期主动基金规模遭遇2.3万亿美元的净流出。背后的原因或许在于ETF的税收优势明显、指数基金的持有成本更低、被动投资的流动性和透明度更高,但美国投资者对主动基金创造alpha收益的信心下滑也是重要的驱动因素。事实上,2023年底的最新数据显示美国被动基金的资产总规模已超越主动基金。
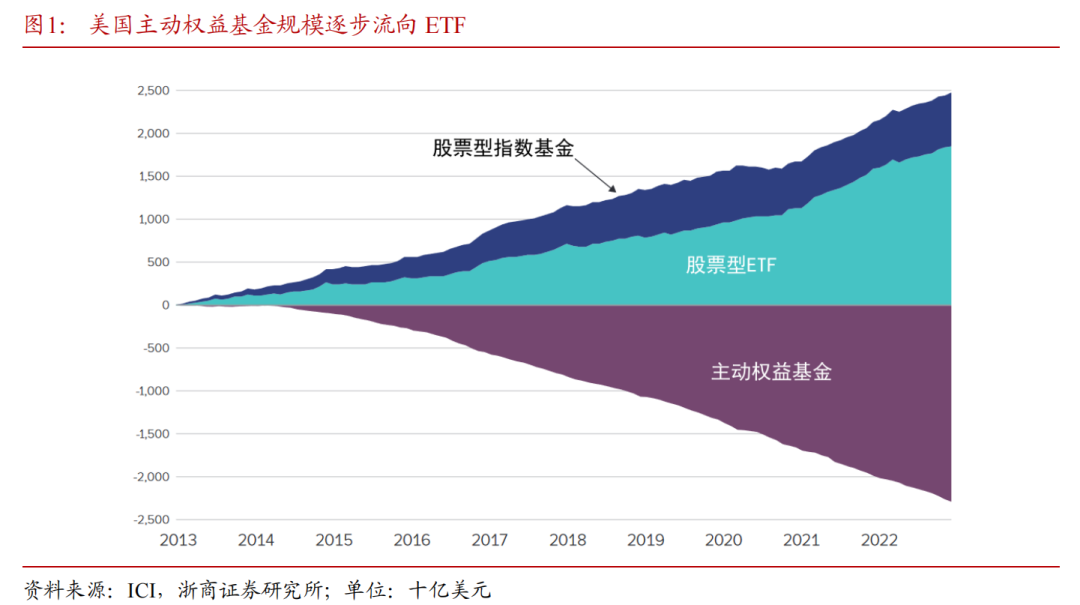
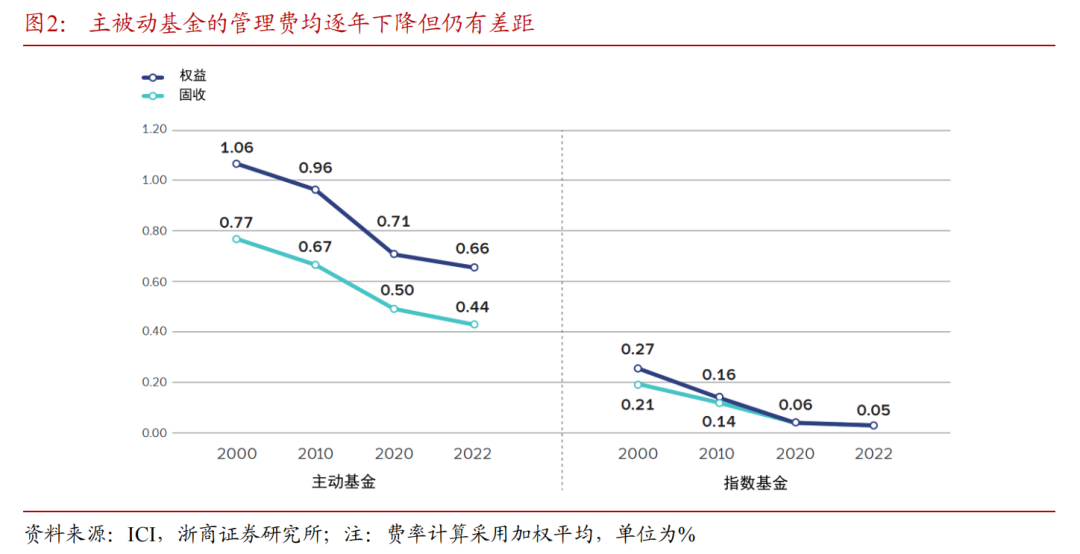
在此背景下,作为重要的投资品种,主动基金究竟能否创造alpha收益?怎样科学严谨衡量alpha收益强弱?定量上有多大比例的基金具备alpha收益能力?上述三大问题是本期学界纵横所要讨论的话题。
02
核心结论
事实上,基金能否获取有效的alpha收益也是多年以来学术界持续争论的话题。Kosowski等人(2006) 和Fama &French(2010)(以下分别简称为KTWW(2006)和FF(2010))在论文中均对该问题有过深入讨论,值得关注的是两者虽然通过相同统计方法(bootstrap),却得到了截然相反的结论。KTWW(2006)认为有超过10%的美国主动基金是存在显著alpha,而FF(2010)则认为该比例不超过1%。
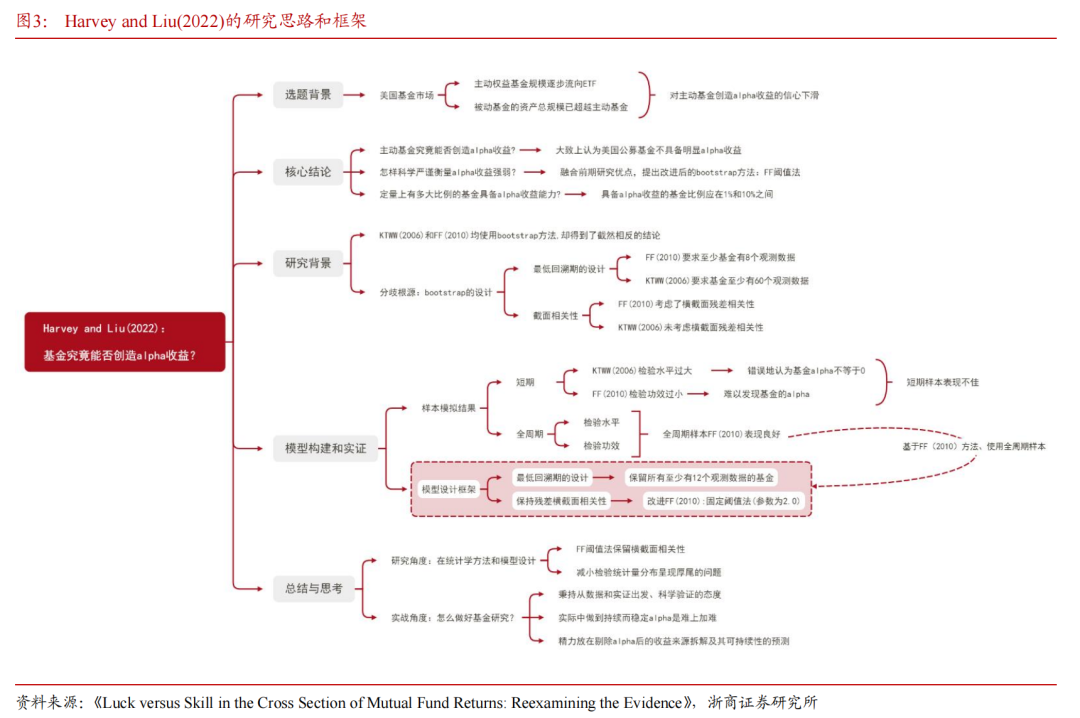
本篇报告推荐的学术文章是由CAMPBELL R. HARVEY 和YAN LIU合作的《Luck versus Skill in the Cross Section of Mutual Fund Returns: Reexamining the Evidence》(下文中简称为Harvey and Liu(2022)),于2022年入选金融学顶刊Journal of Finance。Harvey and Liu(2022)指出KTWW(2006)和FF(2010)的方法并不完善,研究的关键在于如何更加严谨合理的设计和构建bootstrap方法和检验模型。
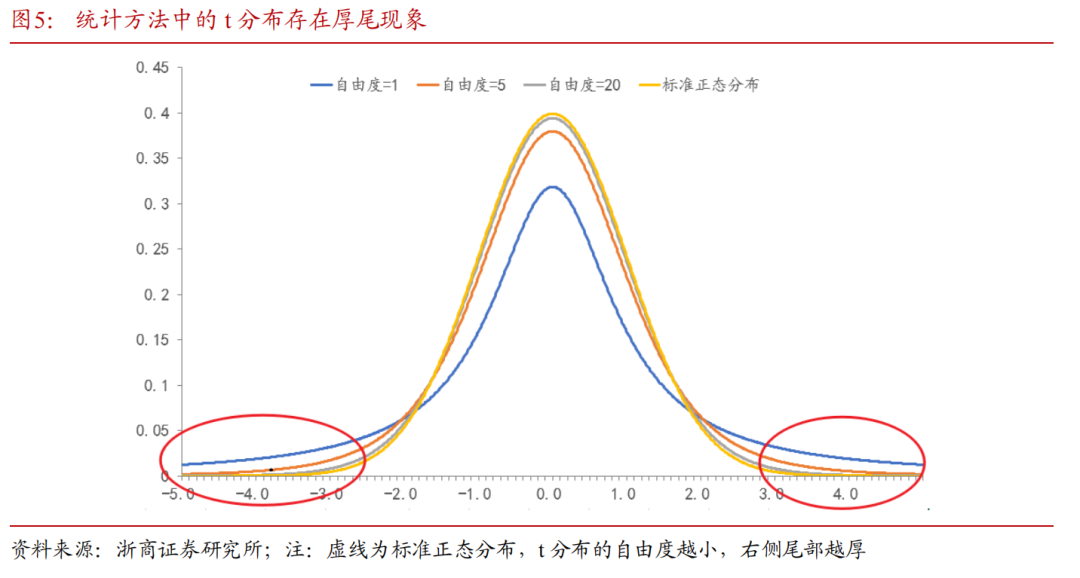
Harvey and Liu(2022)通过一系列模拟实验发现KTWW(2006)所用方法过度拒绝了原假设(原假设为所有基金的alpha等于0),使得在所有基金都没有超额收益的情况下,依然拒绝了原假设,换言之,过度乐观地认为美国主动基金存在显著alpha收益;而FF(2010)所用方法使得bootstrap检验统计量分布呈现厚尾现象,在基金有alpha的情况下,错误地接受了原假设,换言之,可能低估了基金的alpha收益能力。
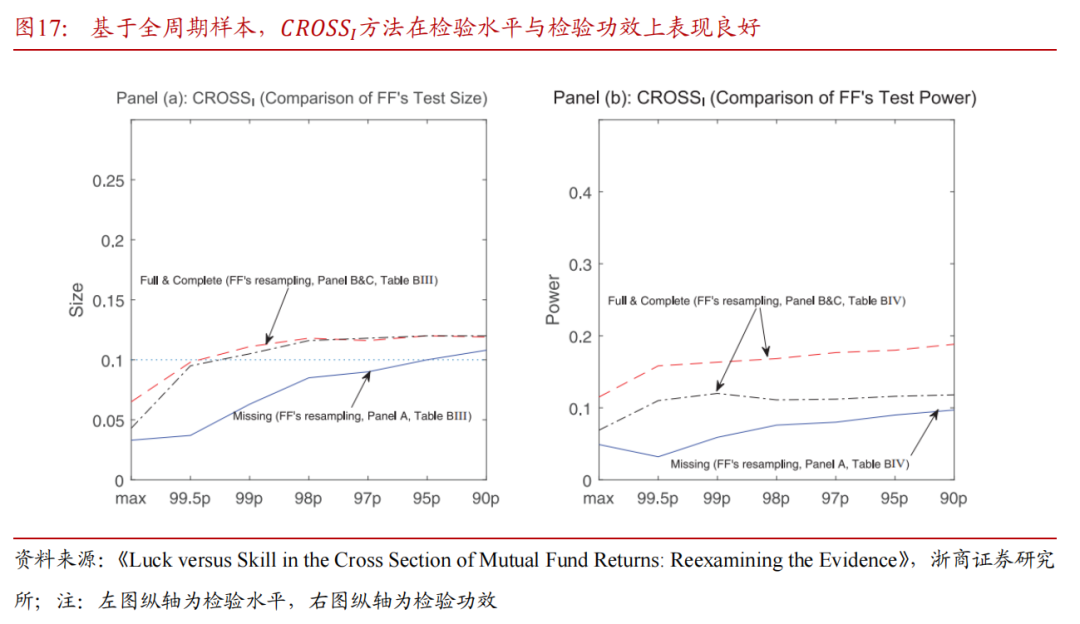
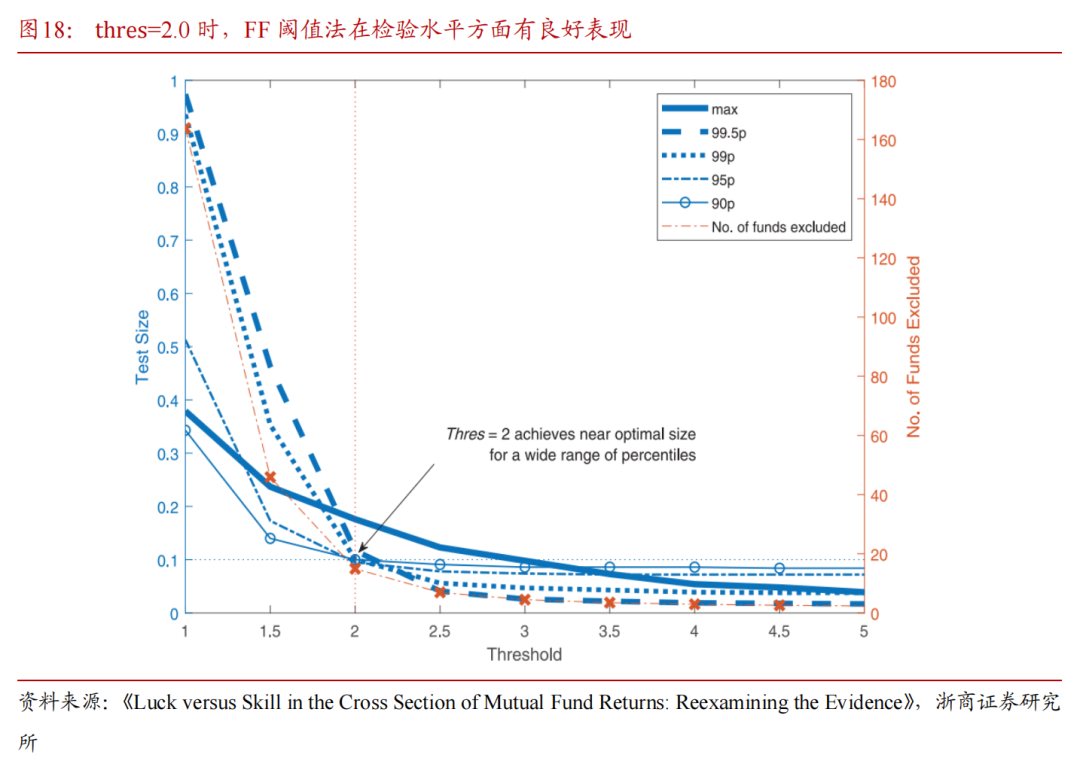
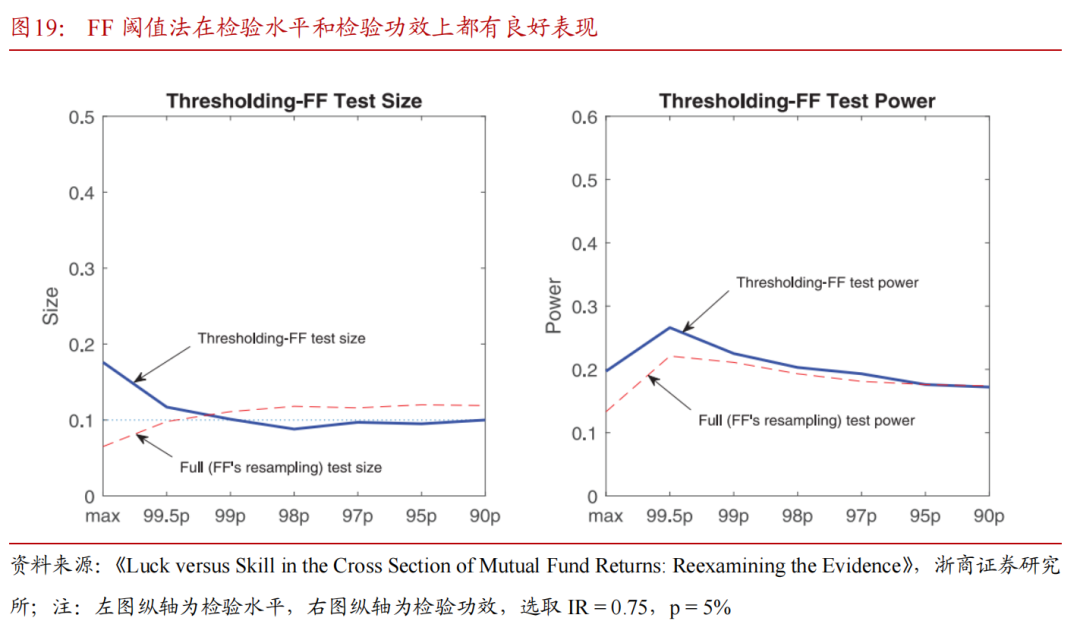
Harvey and Liu (2022) 综合以上两种bootstrap方法,融合二者的优点,在保留横截面的相关性基础上对FF(2010)方法进行了改进,提出了一个改进方法——FF阈值法,并通过模拟实验证明了改进的方法在检验水平和检验功效两方面上都有优良表现。最终得出结论:整体认为美国主动基金不具备明显alpha收益,改进后的实证结果表明有显著alpha的基金比例应介于FF(2010)的1%和KTWW(2006)的10%之间。
03
研究背景:KTWW(2006)、FF(2010)
在该领域过往的研究中,KTWW(2006)和FF(2010)都曾给出基金能否创造alpha收益的结论。从学术研究角度,关于基金能否创造alpha收益这个问题,原假设应设置为:所有基金alpha等于0。在这个共同的原假设下,首先构造一个alpha恰好为0的伪基金样本,然后将其视为总体,并用bootstrap方法进行重采样,生成原假设下的检验统计量(即t-统计量)的横截面。为了总结横截面中的信息,Harvey and Liu (2022)主要关注检验统计量横截面的极端百分位数(例如,第90百分位数),再通过bootstrap方法,获得一个百分位统计量的经验分布。如果实际数据的百分位统计量太大,我们就有理由拒绝原假设,并得出基金存在alpha收益的结论,反之则接受原假设。
3.1 什么是bootstrap方法?
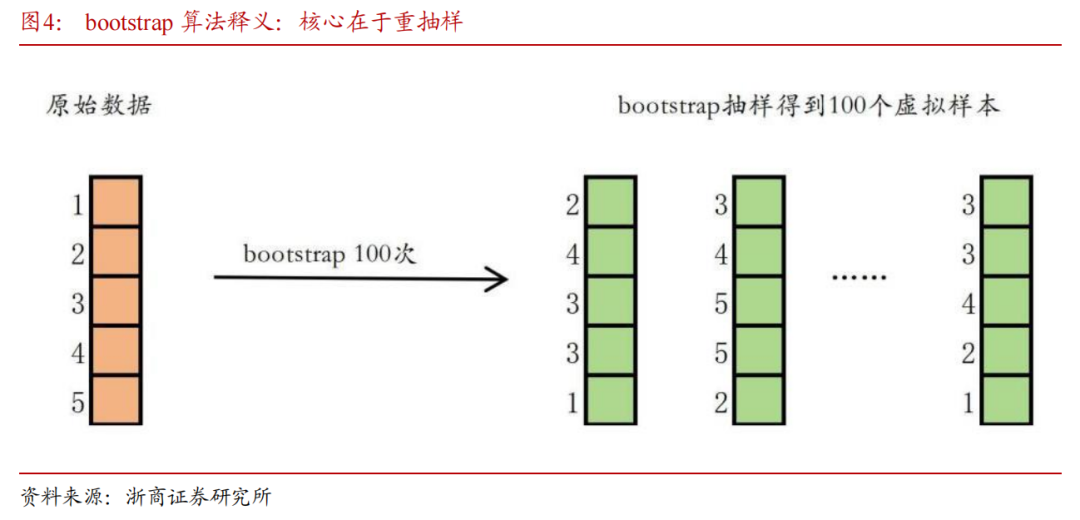
简单介绍以往的研究和本篇文献所使用的bootstrap方法。bootstrap方法是一种统计学中的重抽样技巧,它通过从原始数据集中有放回地抽取样本,生成多个虚拟样本集来估计统计量的分布。假设原始数据有n个,想获得原始数据的某些统计量,但可能由于原始数据样本量较小、总体分布不明确等原因,难以直接获得较好的结果。此时就可以使用bootstrap方法,从原始数据中有放回地抽取n个样本,构成一个新的虚拟样本。这个过程重复B次后生成B个虚拟样本集。
用一个具体的例子说明:假设原始数据为1,2,3,4,5(n=5),用bootstrap方法有放回抽样100次(B=100),得到虚拟样本。bootstrap方法的优势在于,它不需要对总体分布做出假设,而是用经验分布替代总体分布。bootstrap方法简单易行,常用于计算置信区间、估计标准误差以及进行假设检验等。
3.2 分歧的根源:bootstrap 设计
KTWW(2006)和 FF(2010)在 bootstrap 方法具备两大主要区别:最低回溯期设计、截面相关性的考察。
3.2.1 最低回溯期
FF(2010)要求基金有8个收益率的观测数据即可,但KTWW(2006)要求基金最低具有60个收益率的观测数据。bootstrap方法通常只在收益率有观测数据的样本中进行(称传统方法,这是KTWW(2006)的主要方法),FF(2010)的方法与传统方法不同,它们在任何时间点重新取样整个截面,但这样会导致一些基金缺少观测数据。因此,对某一特定基金的bootstrap样本的观察次数可能与实际样本中的观察次数不同,导致FF(2010)方法与传统方法(不包括缺失值的观测数据)的t-统计量分布不同。
FF(2010)所用方法中不完善的环节是欠采样。FF(2010)方法潜在问题是,在模拟实验中,过采样(bootstrap样本中观测数据 > 实际观测数据)基金的数量应该近似等于欠采样(bootstrap样本中观测数据 < 实际观测数据)基金的数量,过采样和欠采样的t-统计量分布可能非常不同。具有自由度D的t分布在D较大时收敛于标准正态分布,因此过采样的问题不大,而欠采样会出现问题。例如,对于具有T = 24实际观测数据的基金,过采样(例如,T = 36)不太可能出现问题,因为T = 24和T = 36的t统计量分布相似;而欠采样(例如,T = 12)会导致厚尾现象(即尾部分布比正态分布大)。即观测的月份数越少,则厚尾效应越强,统计量难以显著。
考虑到FF(2010)对缺失数据的bootstrap方法,对于历史收益数据较短的基金,可能会出现抽样次数较少的情况,为确保有足够的样本量,FF(2010)要求在原始样本或bootstrap样本中至少有8个收益率的观测数据。
这里文章举例说明过采样和欠采样的非对称影响。文章随机选取一个有T个月观测数据的基金,将其收益率减去alpha的估计,然后通过bootstrap 100万次产生三组分布。在第一组中,文章通过FF(2010)方法生成了bootstrap样本中观测次数的分布。在第二组中,文章比较了两种方法的t-统计量的bootstrap 分布:一种是“完整数据bootstrap”(KTWW(2006)的做法),该方法仅对实际有基金收益进行重新抽样;另一种“缺失数据bootstrap”(FF(2010)的做法),该方法重新抽样所有时间段,包括基金缺失观测数据的时间。在最后一组中,对于“缺失数据bootstrap”(FF(2010)的做法),将其t-统计量的bootstrap分布分解成过采样和欠采样下的分布。
1)测算周期过短时(T=13),“缺失数据bootstrap”分布不对称,当T=23时,bootstrap分布在23处达到峰值且大致对称,且bootstrap分布横轴的变化范围很大(从11到约42)。
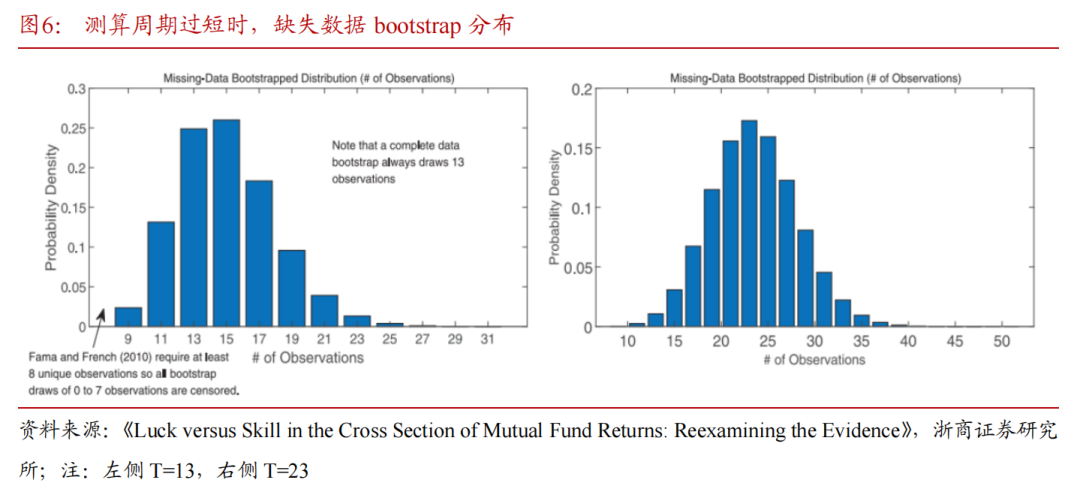
2)t-统计量较大的部分(即t-统计量≥5)与FF(2010)方法更相关,FF(2010)方法检验了t-统计量的横截面分布的右尾。为了更好地总结右尾的信息,文章还将t-统计量等于10处的分布进行了筛选,当t统计量大于10时,其分布是相当分散的。可以观察到,“缺失数据bootstrap”产生大t-统计量的概率都高于“完整数据bootstrap”方法,扭曲了t-统计量的分布,使得FF的方法获得的检验统计量难以显著。
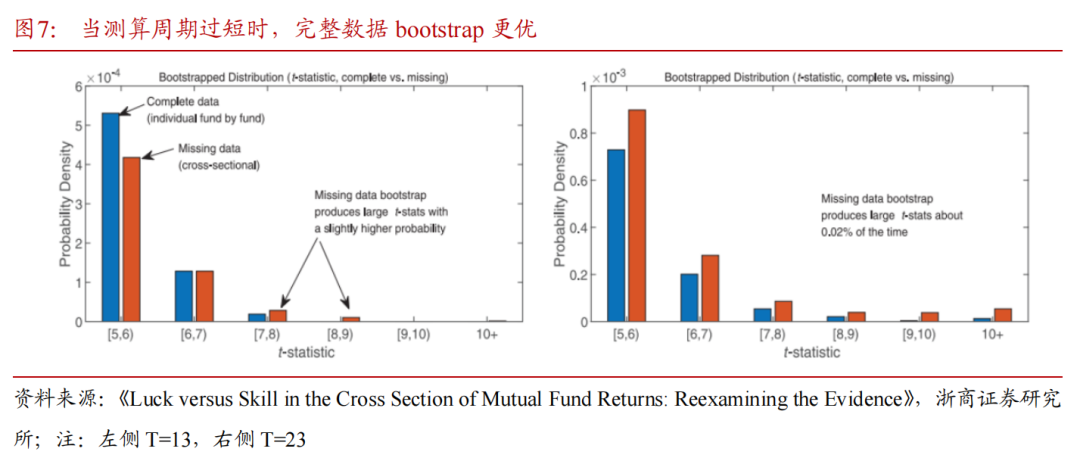
3)文章对FF(2010)bootstrap分布的过采样和欠采样进行了分解。可以看到欠采样产生更大的t-统计量的概率一致大于过采样,使得检验统计量难以显著。
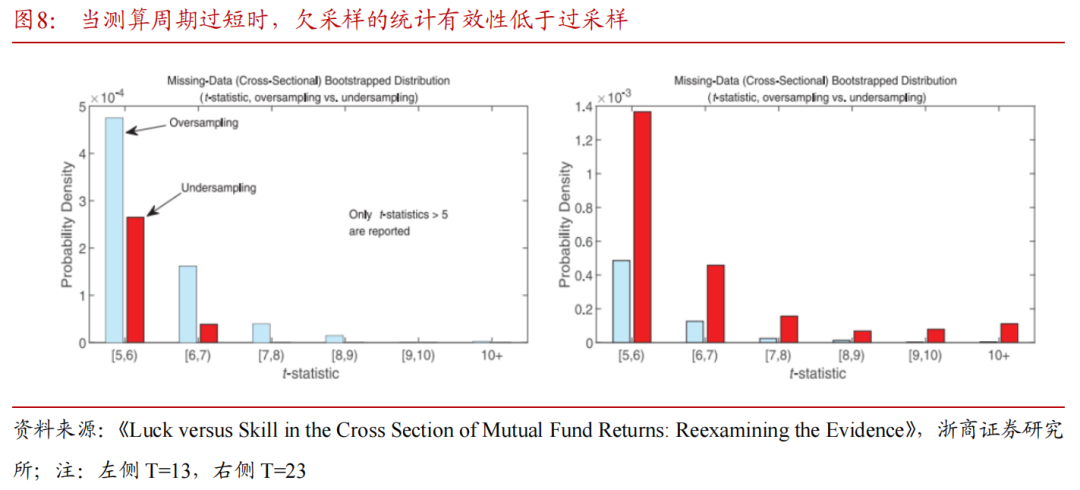
4)总之,“缺失数据bootstrap”和欠采样会带来的不良影响。首先,“缺失数据bootstrap”比“完整数据bootstrap”更容易获得大的t-统计量。其次,在其他条件相同时,欠采样比过采样更容易获得大的t-统计量。而当测算周期长时,“完整数据bootstrap”和“缺失数据bootstrap”之间的差异要小得多,尽管T = 36的过采样和欠采样之间仍然存在一些不对称性。
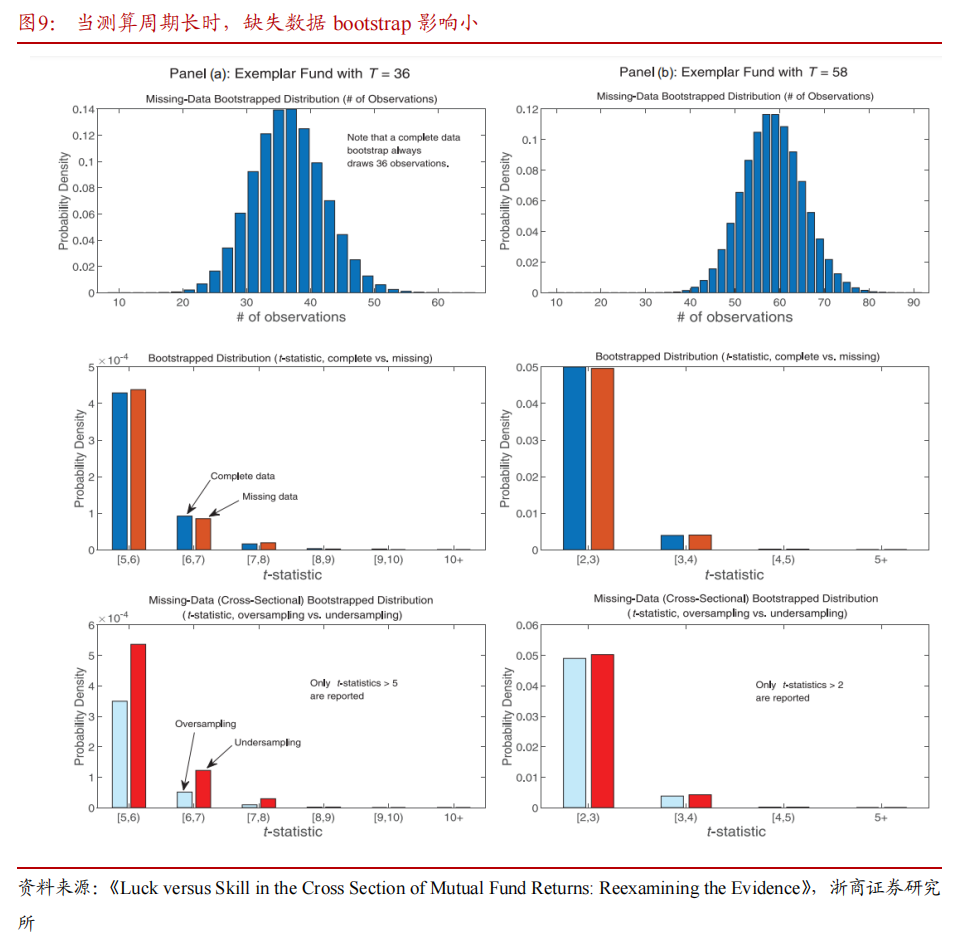
3.2.2 截面相关性
KTWW(2006)和FF(2010)在构建的bootstrap方法时进行的不同处理,以下分别介绍这些不同的bootstrap方法,注意,这些方法在横截面相关性方面有所不同。

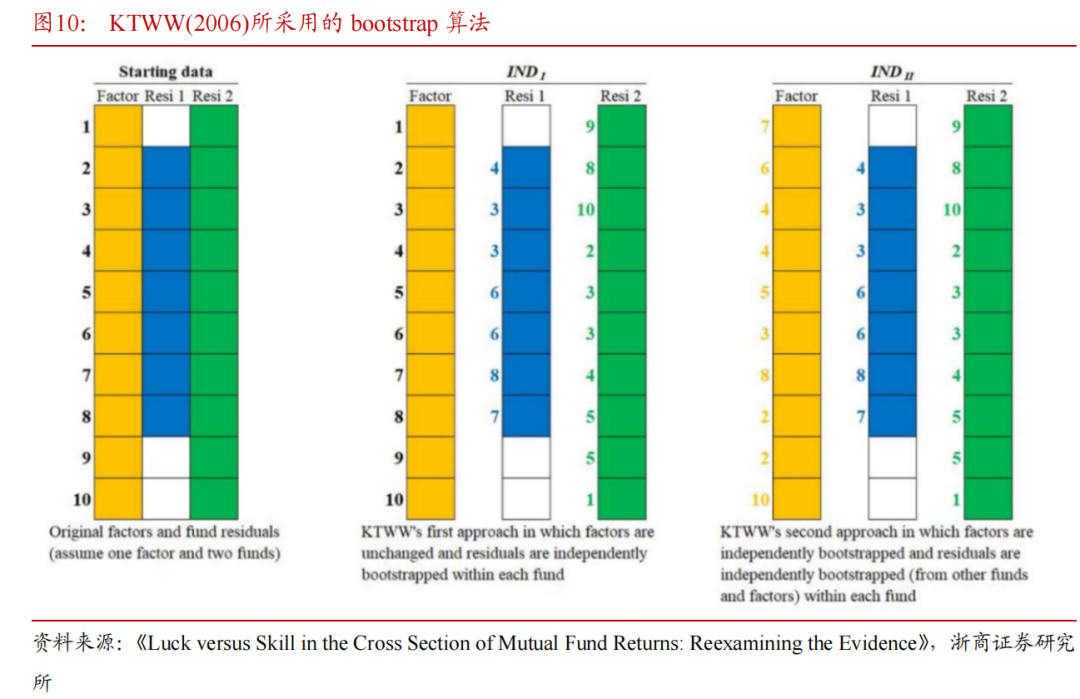

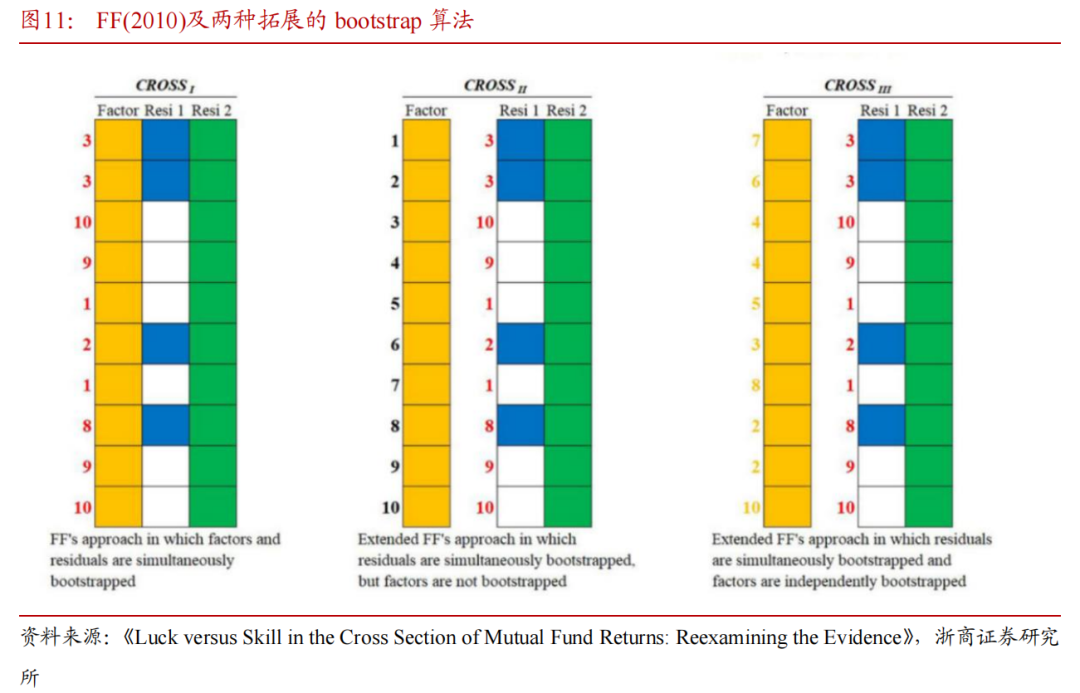
前文中文献详细解释了KTWW(2006)和FF(2010)在构建的bootstrap方法时的差异,基于FF(2010)方法,Harvey and Liu (2022)创新性地提出FF阈值法,下文中我们重点关注如何构建该模型。
04
模型构建和实证结果
文章所用的美国基金数据来自于证券价格研究中心(CRSP)的共同基金数据库。在整个样本中,至少有8个观察数据的基金数量为4007个。由于基金样本大小在bootstrap时起着关键作用,文章在表1中提供了基金样本分布的概况,体现基金样本所包含的观测数据的月份数的分布。
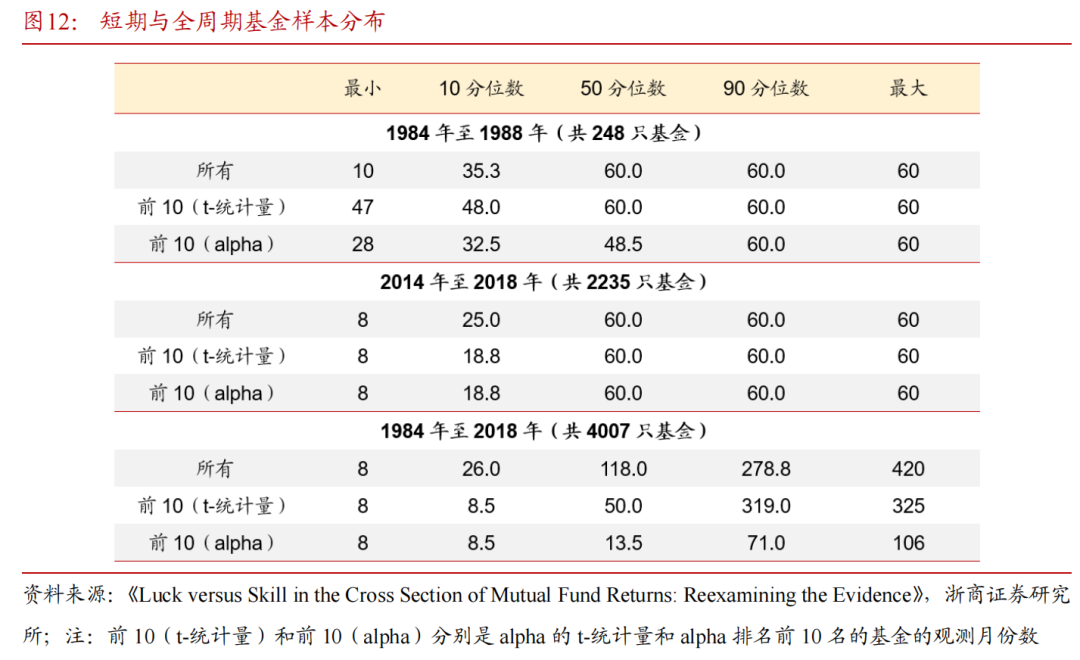
4.1 模型设计的方法和框架
文章在模型设计时需解决两个关键问题:
(1)最低回溯期的设计。选择多长的回溯期为最优?FF(2010)要求基金至少有8个收益率的观测数据即可,但KTWW(2006)要求基金需有60个收益率的观测数据。文章通过权衡各方面因素,最终选择使用有12个收益率的观测数据的基金。
(2)保持残差中的横断面相关性。在FF(2010)方法中,很好地控制了该相关性,所以文章基于FF方法的思路,在模拟设计中使用bootstrap方法来克服这个问题。

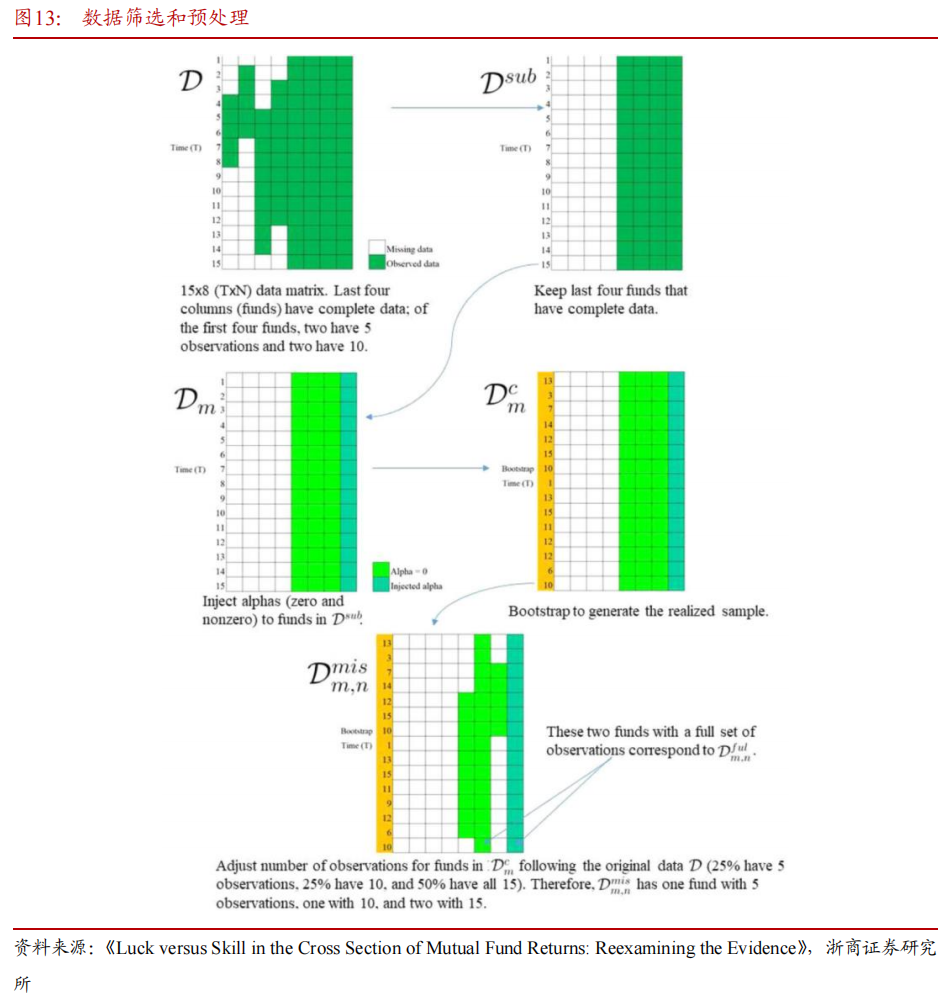
4.2 短期样本的模拟结果
文章分别对KTWW(2006)和FF(2010)进行分析,包括两个短期样本和全周期样本。其中对于短期样本,文章分别考察了最初的五年期间(1984年至1988年)和最后的五年期间(2014年至2018年)。

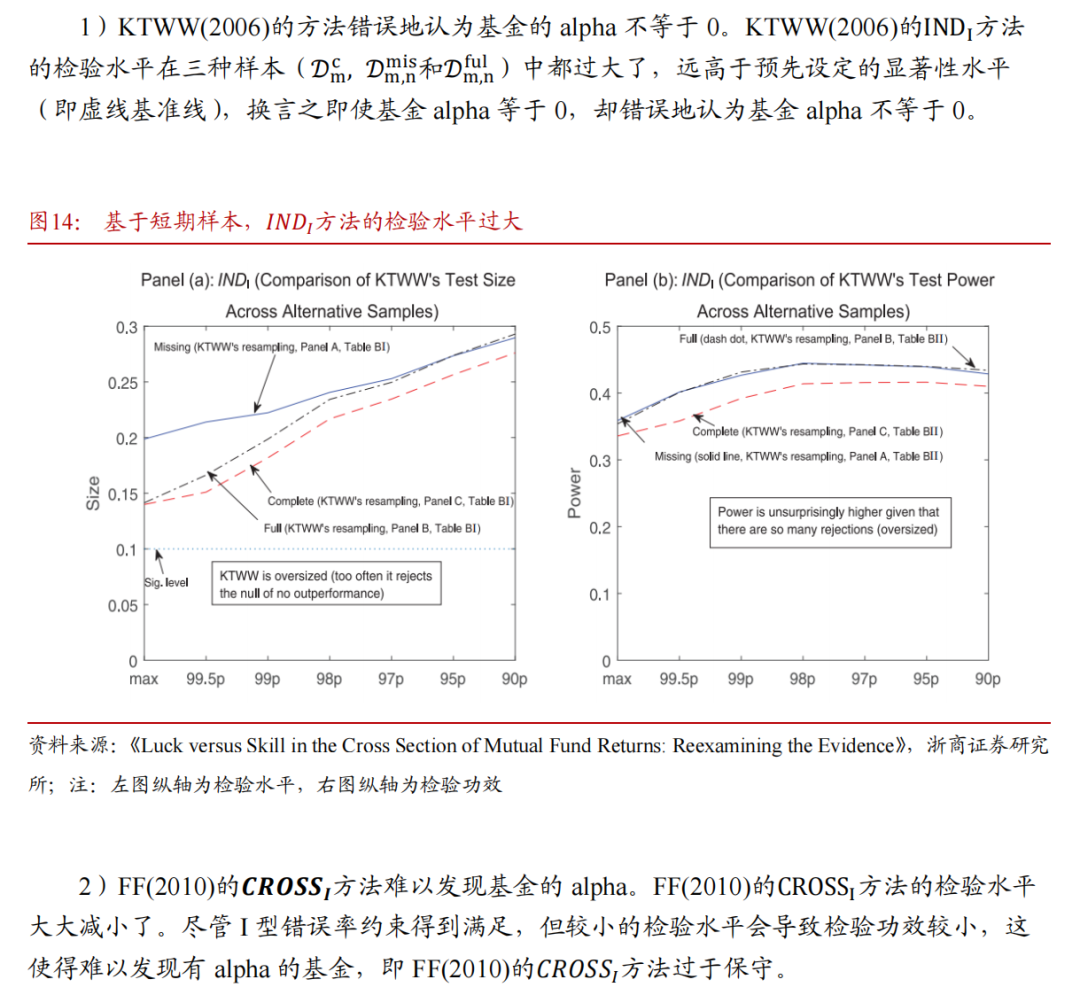
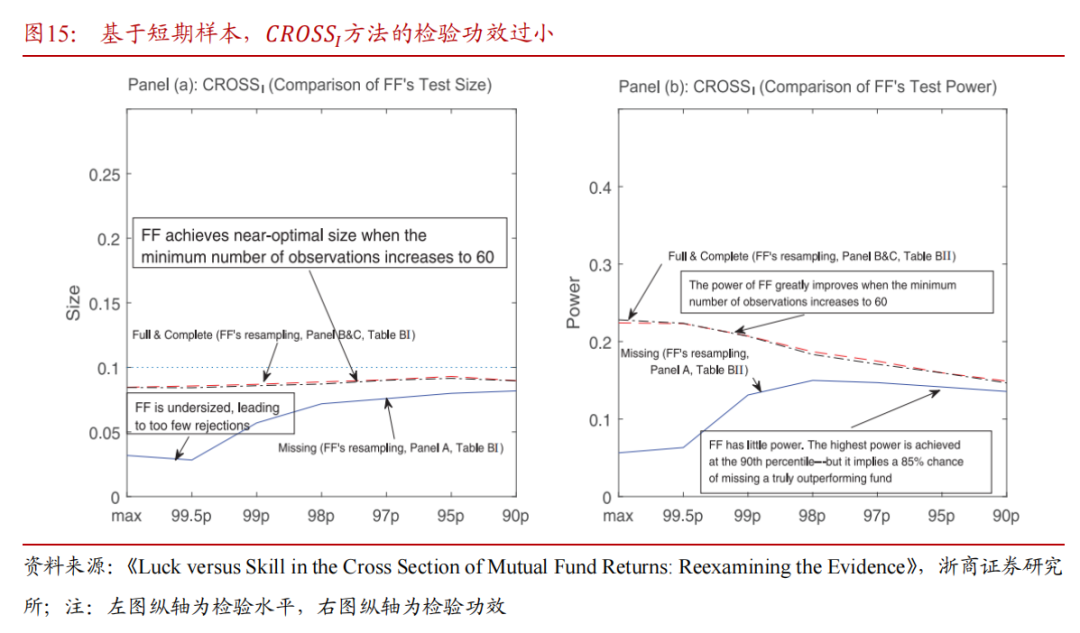
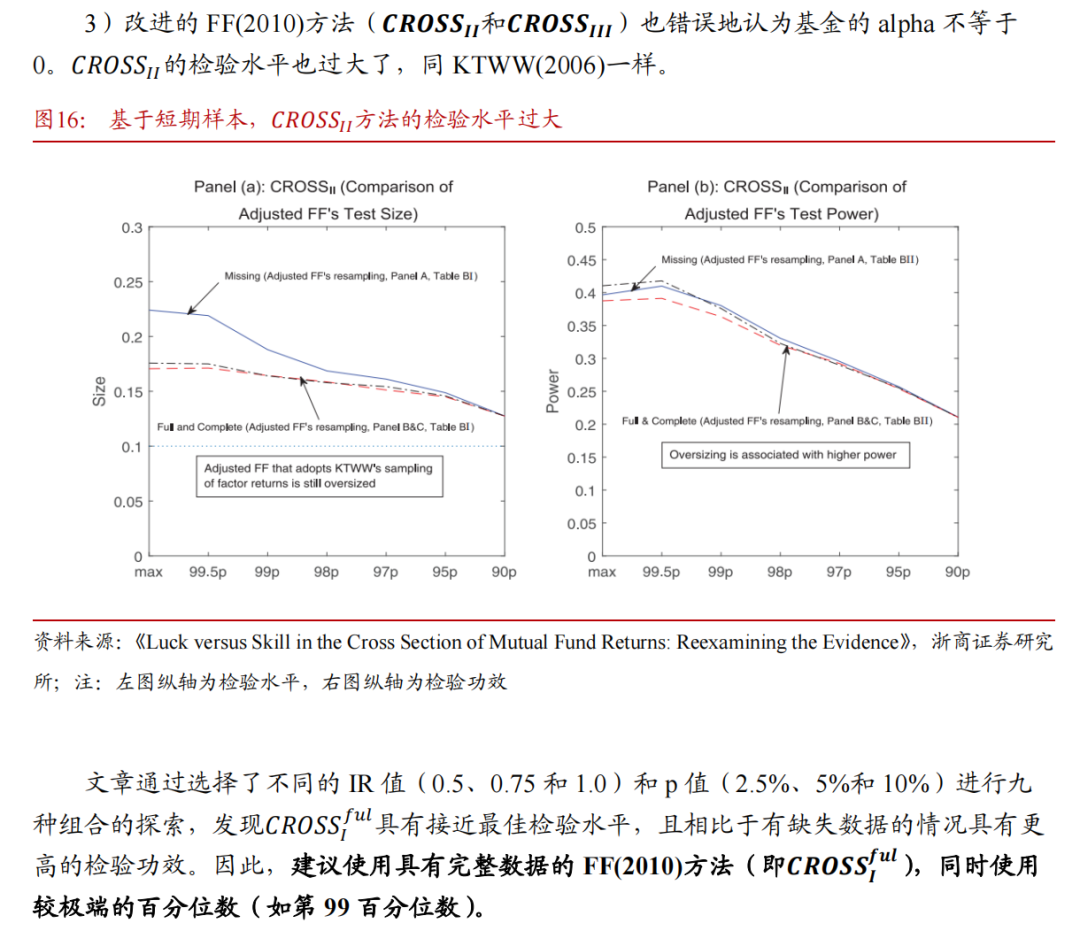
4.3 全周期样本的模拟结果
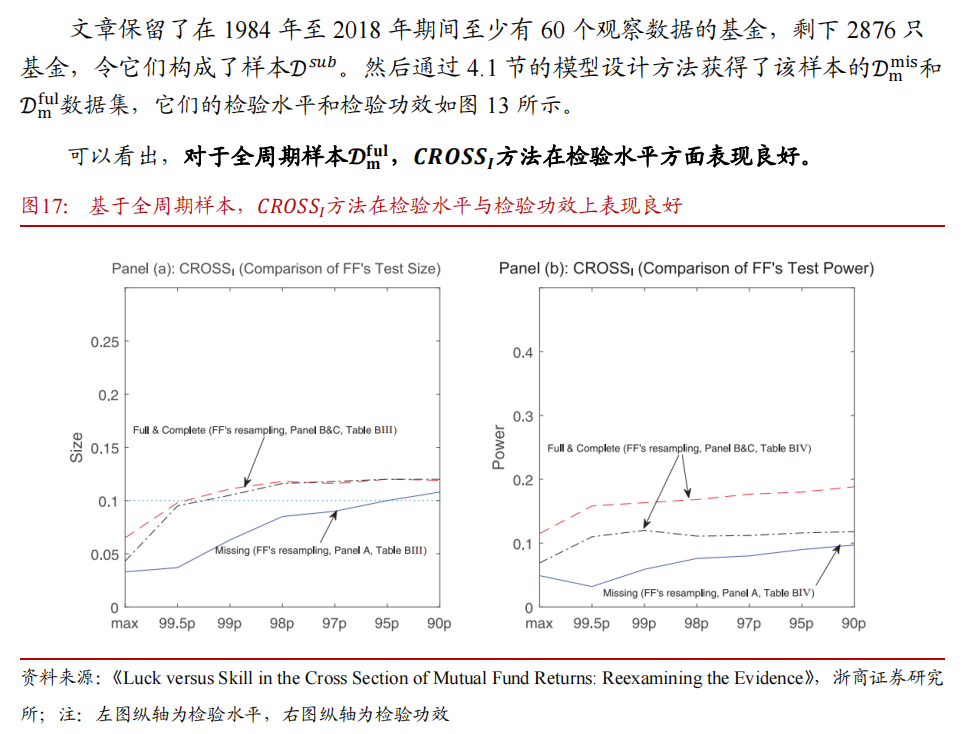
4.4 改进bootsrap方法:FF阈值法

05
总结与思考
面对主动基金较弱的alpha收益,指数基金的强势是美国投资者“用脚投票”的结果,2023年底的最新数据显示美国被动基金的资产总规模已超越主动基金。2013年至2022年,美国股票型指数基金累计吸引了2.5万亿美元的净新资金流入,而同期主动基金规模遭遇2.3万亿美元的净流出。本期学界纵横推荐的文章尝试讨论三个话题:主动基金究竟能否创造alpha收益?怎样科学严谨衡量alpha收益强弱?定量上有多大比例的基金具备alpha收益能力?
“基金能否创造alpha收益”是基金研究学术界的核心话题,Kosowski等人(2006) 和Fama &French(2010)(以下分别简称为KTWW(2006)和FF(2010))的研究成果具备代表性。但是两者通过相同统计方法(bootstrap),却得到了截然相反的结论:KTWW(2006)认为有超过10%的美国主动基金是存在显著alpha,而FF(2010)则认为该比例不超过1%。
Harvey and Liu (2022)在Journal of Finance发表《Luck versus Skill in the Cross Section of Mutual Fund Returns: Reexamining the Evidence》,通过研究和实证表明KTWW(2006)和FF(2010)的方法并不完善,KTWW(2006)的方法过度乐观地认为美国主动基金存在显著alpha收益,FF(2010)的方法过度低估基金的收益能力,得出了过于保守的结论。
Harvey and Liu (2022)综合以上两种bootstrap方法,融合二者的优点,在保留横截面的相关性基础上对FF(2010)方法进行了改进,提出了一个改进方法——FF阈值法。文章通过模拟实验证明了改进方法的有效性并得出结论:整体认为美国主动基金不具备显著alpha收益,改进后的实证结果表明有显著alpha的基金比例应介于FF(2010)的1%和KTWW(2006)的10%之间。
基金研究应秉持从数据和实证出发、科学验证的态度,将精力放在剔离alpha后的收益来源拆解及其可持续性的预测上。研究角度,文献在统计学方法和模型设计上提供了有效思路,比如FF阈值法在处理该多重假设检验问题时,既能保留横截面相关性,同时杜绝检验统计量分布的厚尾问题。实战角度,当统计学表明美国基金不具备显著alpha收益,实际能做到持续而稳定alpha则是难上加难。
06
风险提示
1、文章内容参考了文献《Luck versus Skill in the Cross Section of Mutual Fund Returns: Reexamining the Evidence》,文章内容部分仅代表该文献的观点,不代表浙商金工研究观点。
2、文章模拟实验使用了美国公募基金历史数据,历史表现不代表未来收益,也并不适用于其他市场。
报告作者:
陈奥林 从业证书编号 S1230523040002
肖植桐 从业证书编号 S1230523100003
欢迎小伙伴加入我们,一起思考,
寻找定价逻辑,实现共同富裕。
详细报告请查看2024年1月27日发布的浙商证券金融工程深度报告《学界纵横系列之四:主动基金究竟能否创造alpha收益?》
法律声明及风险提示:
本公众号为浙商证券金工团队设立。本公众号不是浙商证券金工团队研究报告的发布平台,所载的资料均摘自浙商证券研究所已发布的研究报告或对报告的后续解读,内容仅供浙商证券研究所客户参考使用,其他任何读者在订阅本公众号前,请自行评估接收相关推送内容的适当性,使用本公众号内容应当寻求专业投资顾问的指导和解读,浙商证券不因任何订阅本公众号的行为而视其为浙商证券的客户。
本公众号所载的资料摘自浙商证券研究所已发布的研究报告的部分内容和观点,或对已经发布报告的后续解读。订阅者如因摘编、缺乏相关解读等原因引起理解上歧义的,应以报告发布当日的完整内容为准。请注意,本资料仅代表报告发布当日的判断,相关的研究观点可根据浙商证券后续发布的研究报告在不发出通知的情形下作出更改,本订阅号不承担更新推送信息或另行通知义务,后续更新信息请以浙商证券正式发布的研究报告为准。
本公众号所载的资料、工具、意见、信息及推测仅提供给客户作参考之用,不构成任何投资、法律、会计或税务的最终操作建议,浙商证券及相关研究团队不就本公众号推送的内容对最终操作建议做出任何担保。任何订阅人不应凭借本公众号推送信息进行具体操作,订阅人应自主作出投资决策并自行承担所有投资风险。在任何情况下,浙商证券及相关研究团队不对任何人因使用本公众号推送信息所引起的任何损失承担任何责任。市场有风险,投资需谨慎。
浙商证券及相关内容提供方保留对本公众号所载内容的一切法律权利,未经书面授权,任何人或机构不得以任何方式修改、转载或者复制本公众号推送信息。若征得本公司同意进行引用、转发的,需在允许的范围内使用,并注明出处为“浙商证券研究所”,且不得对内容进行任何有悖原意的引用、删节和修改。
廉洁从业申明:
我司及业务合作方在开展证券业务及相关活动中,应恪守国家法律法规和廉洁自律的规定,遵守相关行业准则,遵守社会公德、商业道德、职业道德和行为规范,公平竞争,合规经营,忠实勤勉,诚实守信,不直接或者间接向他人输送不正当利益或者谋取不正当利益。
本篇文章来源于微信公众号: Allin君行