“西学东渐”作为以往学术传播的方式之一,其在如今仍具有重要的现实意义。作为A股市场上以量化投资为研究方向的卖方金融工程团队,我们通过大量的材料阅读,去粗取精,将认为最有价值的海外文献呈现在您的面前。
作为西学东渐——海外文献系列报告第一百五十九篇,本文推荐了Yutong Lu、Gesine Reinert和Mihai Cucuringu于2022年发表的论文《Trade Co-occurrence, Trade Flow Decomposition, and Conditional Order Imbalance in Equity Markets》。
高频交易时间的接近度可能包含着显著的选股信号。在本文中,作者提出了一种根据每笔交易与市场上其他交易的接近度对每笔交易进行分类的方法,并将其分为五种类型。通过构建与各类交易相关的归一化订单失衡指标(称之为条件订单失衡(COI)),作者研究了分解交易流对股票价格的影响。作者的实证研究结果表明:同期收益率与COIs存在显著的正向相关性。在可预测性方面,作者发现如果交易的COIs与其自身以外的股票交易相隔离,那么其与未来收益的关联性为正,反之则为负。此外,作者基于三年数据,运用COIs开发的交易策略对457只股票进行了广泛的实验,回测结果表明该交易策略实现了显著的收益和夏普比率。
风险提示:文献中的结果均由相应作者通过历史数据统计、建模和测算完成,在政策、市场环境发生变化时模型存在失效的风险。
现如今,证券交易所向电子交易的转型在极大程度上重塑了市场的微观结构。由于现如今延迟时间已被降低到纳秒级(O’Hara(2015),Hirschey(2021)),市场参与者的交易策略达到了前所未有的盈利水平。市场中的代理人可以直接提交和取消限价订单。当现有限价订单由市场订单/可市场化限价订单执行时,交易即进行结算。携带不同信息的交易对相关股票的价格变化产生不同的影响,学者和从业人员因此将交易分为不同类型,并分别进行研究。例如,按交易方向分组,Chordia、Goyal和Jegadeesh(2016)研究了买卖双方发起的交易流程,将其分为激进买入和激进卖出。Kraus和Stoll(1972)以及Lee等人(2004)将机构与个人投资者交易分开。与上述完全基于单个交易特征的分类不同,我们感兴趣的是根据交易的投放时间相对于整个市场上其他交易的到达时间进行分类,既包括同一资产内的交易,也包括横截面上的交易。市场参与者可以通过观察市场上的交易流向来做出交易决策,这就是我们研究的动机所在。以前的研究(Kyle(1985)、Kyle、Ou-Yang,和Wei(2011))对高频率价格的形成进行建模,并指出交易者将大订单拆分成许多小订单以掩盖其真实目的,其他市场参与者则会监控市场中的订单流以便做出交易决策。高性能交易系统的发展导致了高频交易(HFT)的惊人增长,并提高了交易策略的多样性(Hagstromer and Norden(2013))。在这个世界上,反应时间起着重要作用,因为如果不在微秒甚至纳秒内采取行动,机会就会瞬息万变。高频交易策略包括预测交易流(Hirschey(2021))和掠夺其他市场参与者(Van Kervel和Menkveld(2019))。我们有兴趣探讨的问题是:某些交易是否会与其他交易发生相互作用?交易是否包含有用信息?它们是如何促进股价变动的?这些问题有助于我们揭示短期和长期的价格形成机制。我们首先提出第3.1节中定义的“交易共现”概念,其是可以根据交易与其他交易之间的互动关系对交易进行识别和分组的一种工具。对于每笔给定的交易,如果两笔交易发生的时间很近,我们就认为这两笔交易同时发生并相互影响。为了定义和量化“发生时间的邻近度”,我们预先定义了领域大小δ。如果两笔交易的时间差小于δ,则两笔交易邻近且同时发生。注意阈值δ是一个重要参数,它决定了同时发生的交易集合。然而,并没有严格的规则来设定这个值。直观地说,考虑到HFT以机构交易者为猎物并根据机构市场订单进行交易的情况,我们目标是捕捉这些互动,并将此类交易归类为积极互动交易等类别。考虑到这一点,适当的选择应大于往返延迟加上HFT检测和做出交易决策的时间,而这一时间通常是不公开的。因此,我们试验了多个δ值,并对比了相应的结果。需要注意的是δ值也不宜过大,因为过大的邻域很可能会将市场中不相关的交易纳入其中。在本文中,我们将δ视为一个超参数;为简单起见,我们仅在正文中展示了δ= 500µs的经验结果,并在附录A中对不同的δ值选择进行了比较。利用交易共现性,我们通过将所有股票的所有交易分为子组。对于某笔交易,我们通过以下两个问题来确定它属于哪一组:它是否与其他交易互动?如果是,它是否只与自己相同的股票互动,还是只与自己不同的股票互动?还是两种都有?根据答案,交易将被归入一个或两个类别,具体规则将在第3.2节中说明。标记所有交易后,我们研究收益与交易子组之间的关系。我们使用订单失衡作为连接交易流和股票收益的桥梁,这在金融文献中已有深入研究。库存范式(Stoll(1978)、Spiegel和Subrahmanyam(1995),Chordia、Roll和Subrahmanyam(2002))认为在中介市场中,买方发起的交易与卖方发起的交易之间的差额,即所谓的不平衡,会对做市商的库存造成压力。作为回应,做市商会调整存货以维持其市场风险,从而推动价格向一个方向变动。接下来,我们在每日层面上研究了正常交易期间各类交易的总订单失衡属性及其与个股收益率的关系。数据调查表明,所有类别的条件性和无条件订单失衡都是正自相关的。条件订单失衡(COIs)都与原始订单失衡有很强的正相关性。但是条件性和无条件订单失衡之间不一定高度相关。我们的实证结果主要集中在失衡与收益的关系上。通过回归分析,我们发现订单失衡与当日价格变化之间存在显著的正相关关系。此外,与标准回归分析相比,多元回归设置中分解订单流可显著提高adjusted R2,这说明对当日股票开盘到收盘的回报有更加的解释力。为了利用可预测性,我们使用相同的回归分析将订单失衡与未来一天的收益进行拟合。与同期结果不同的是,统计意义上的显著关系只出现在一小部分股票中。尽管有意义的回归系数比例较低,但我们观察到,对于那些与市场其他部分有较高互动的交易,订单失衡似乎与未来收益率呈负相关。相反,对于与市场中其他股票隔离的交易,其订单失衡与未来收益率显示出微弱的正相关。这些关联在我们随后的投资组合分析中得到了进一步证实,具体如下。我们利用这些失衡来构建交易策略。为了评估交易流分解方法的经济价值,我们以 COIs 为信号构建了信号排序投资组合。特别是,如果我们根据在预测回归中观察到的模式做出多空决策,我们将在投资组合中获得收益,最高的年化夏普比率达到2.38。作为基准,我们建立了投资于未分解订单不平衡的投资组合,其夏普比率为负值。本文的其余部分安排如下。第2节概述了我们对金融文献的贡献。在第3节中,我们介绍了交易共现、交易流分解和COIs的定义。在第4节中,我们以描述数据源并进行探索性分析开始我们的实证研究。随后,我们在第5、6节和第7节中分别揭示了COIs与同期收益率之间的关系和COIs的经济价值。第8节提供了稳健性分析和其他实证结果。最后,在第9节中,我们总结了研究结果,并讨论了局限性和未来的研究方向。
本文在三方面对文献有所贡献。首先,我们的研究利用了一种新的共现分析的金融应用,这种统计方法被证明在空间模式分析中非常强大,并广泛应用于生物学(Gotelli(2000)、MacKenzie,Bailey和Nichols(2004)、Ara´ujo etal.(2011)、自然语言处理(NLP)(Dagan、Lee和Pereira(1999)、Kolesnikova(2016))、计算机视觉(Galleguillos、Rabinovich和Belongie(2008)、Aaron、Taylor和Chew(2018))等领域(Appel和Holden(1998)、Ye等人(2017))。到目前为止,共现分析在金融文献中的应用主要集中在研究新闻报道中的股票共现。Ma、Pant和 Sheng(2011)从在线新闻中的公司共现构建网络,并使用机器学习模型来识别公司之间的竞争关系。最近的研究,包括Guo等人(2018);Tang、Zhou和Hong(2019);Wu等人(2019)利用新闻中的股票共现构建网络,并将其用于股票回报率预测和投资组合分配等任务。我们的贡献在于提出了交易共现的概念。通过直接应用股票交易的共现性,我们发现这种技术有利于探索和洞察金融市场的微观结构。其次,我们的研究为市场中交易活动之间相互作用添了新的内容。在Kyle(1985)的模型中,做市商通过观察市场中知情交易者和流动性交易者的总订单流来调整自己的交易策略。更激进的是,HFT交易者可以发现机构等知情交易者(Van Kervel和Menkveld(2019)),并预测其他人的交易流向(Hirschey(2021))。各种理论模型(Grossman和Miller(1988)、Brunnermeier和Pedersen(2005)、Yang和Zhu(2020)和Zhu (2020))就高频交易者和机构交易者之间的相互作用提出了各种理论模型。Van Kervel和Menkveld(2019)对瑞典股市进行了实证研究,发现当机构交易者开始拆分大单时,HFT 参与者打算逆风交易,最终与机构同向交易。我们提出“交易共现性”这一概念,并提供了实证证据,证明股票交易的共现性并非巧合。我们不是研究交易者之间的互动,而是创新性地将交易共现作为一种工具,用于分析单个交易层面的互动性。我们对共现条件的COIs的研究表明,细粒度的交易互动传递了价格形成的有用信息。最后,本文对有关订单失衡和价格形成的文献有所贡献。根据开创性的研究,订单失衡的持续性可以通过两种方式产生。首先,正如Kyle(1985)的模型所指出的,交易者有意在一段时间内拆分大额订单,以尽量减少其对市场的影响,这就导致了自相关失衡。Scharfstein和Stein(1990)指出,订单失衡的另一个来源是羊群效应。为了探讨订单失衡如何影响价格变化,Chordia和Subrahmanyam(2004)提出了一个理论模型,解释订单失衡与同期股票回报之间的正相关关系,这种关系是由做市商动态地适应订单失衡而产生的。此外,全权委托交易商跨日优化拆分订单使订单失衡具有很强的正自相关性和对未来回报的预测能力。他们使用纽约证券交易所(NYSE)上市股票1988年至1998年10年间的日度数据进行了实证研究,证实了他们的理论结果,并表现出使用订单失衡作为交易信号的盈利能力。然而,在可预测性方面还存在争议。例如,Shenoy和Zhang(2007)和Lee等人(2004)发现订单失衡对未来回报没有显著的预测能力。虽然Chordia和Subrahmanyam(2004)没有对交易流进行区分,但随后的研究表明,由不同代理人在不同时间下达的具有不同属性的有价订单会对价格变化产生不同的影响。他们发现(Lee等人(2004)、Bailey等人(2009)、Zhang、Gu、和Zhou(2019)),在中国市场交易者类型的私人识别数据是可用的,同时有迹象表明,机构交易流的订单失衡比个人交易者的失衡对价格的压力更大。在美国市场,Cox(2021)最近对2015年至2016年期间标准普尔500指数股票的研究也得出同样的结果,该研究根据交易是否属于由机构采用的市场间扫盘,将交易分为二元类别(Chakravarty等(2012))。我们的研究利用Covid-19发生前最近一段时期的数据来补充美国市场秩序失衡的研究,并提出了一种无需额外私人数据集即可分解无条件贸易流的新方法。我们的研究表明,在不区分交易的情况下,订单失衡不再对未来回报具有预测能力,这是过去几十年市场微观结构演变的证据(Chordia、Roll和Subrahmanyam(2002;Chordia和Subrahmanyam(2004))。不过,用我们提出的方法分解的贸易流具有不同的信息量且其COIs确实具有预测能力。
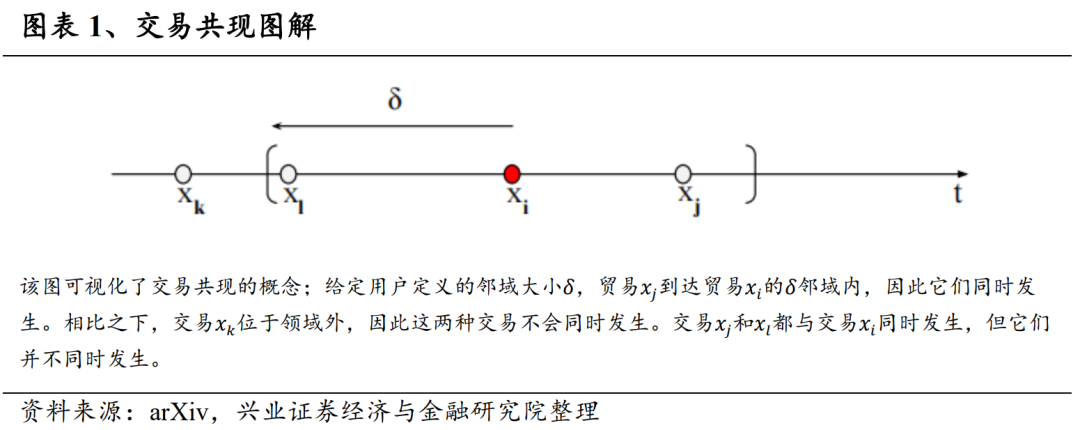
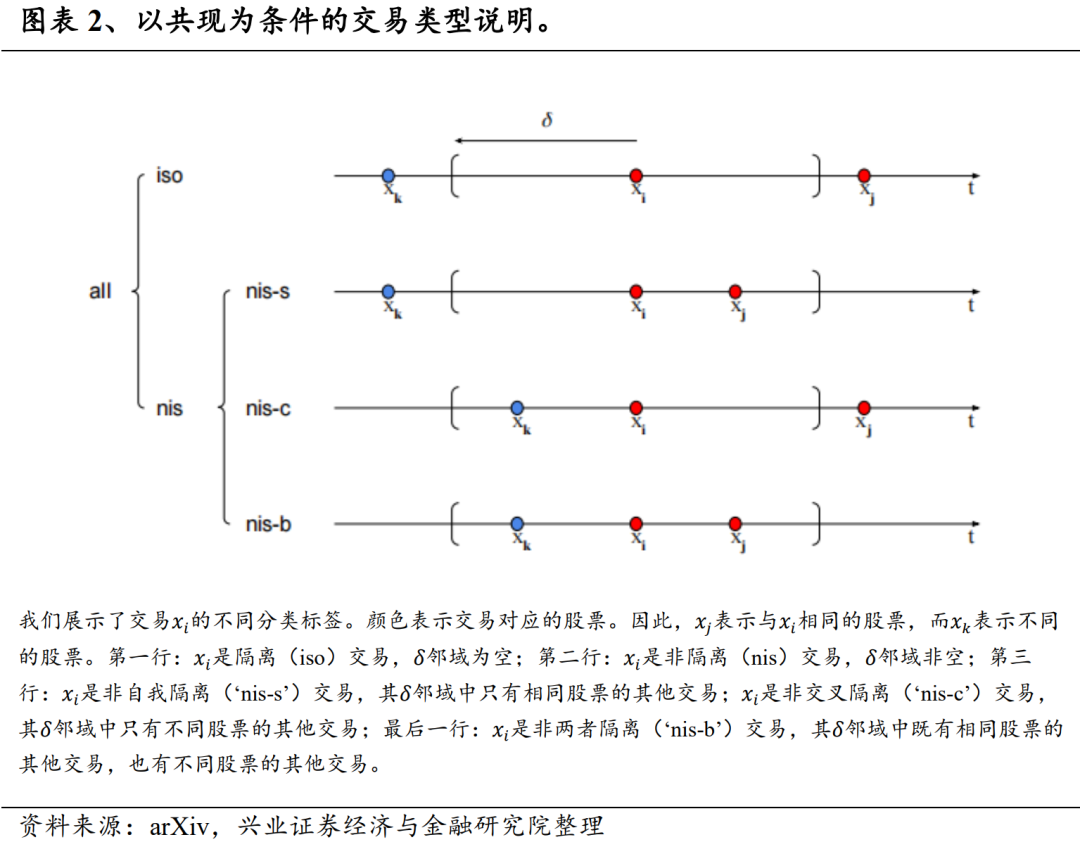
我们首先介绍交易共现的定义。对于在时间发生的每笔交易xi,在预先指定的δ下,除xi本身外,在时间段(t-δ,ti+δ)内到达的每笔交易都被定义为与xi交易共同发生。我们将阈值δ称为“邻域大小”,将与xi同时发生的所有交易集合称为交易xi的“δ-邻域”。我们注意到,共同出现并不是等价关系。xi和xj完全有可能同时出现,而xi和xl也完全有可能同时出现,但xj和xl并不能同时出现。根据共现性,我们接下来将交易分成不同的类别,这些类别以δ邻域为特征,其协议如图表2。最初,我们将所有交易分为两组:隔离交易(iso)和非隔离交易(nis)。如果这笔交易不与其他交易同时出现,则标记为隔离交易。否则,交易将被标记为非隔离交易。我们根据其δ邻域内的交易属性进一步分解非隔离交易。1. 非自我隔离(nis-s):交易xi的δ邻域只包含与交易xi(至少一个)相同股票的交易;2. 非交叉隔离(nis-c):交易xi的δ邻域只包含与交易股票xi不同的股票交易;3. 非两者隔离(nis-b):交易xi的δ邻域既至少包含一个相同股票的交易,也至少包含一个不同股票的交易。这三类交易构成了非隔离交易集的分区,如图表2最后一行所示。我们将这种将交易分门别类的过程称为“交易流分解”。在对交易流量进行分解后,我们开始研究具有不同特征的交易对价格的影响。连接交易活动和价格变化的桥梁是订单失衡量,它被定义为买卖双方发起的交易量之间的归一化差额(Chordia和Subrahmanyam(2004))。对于给定的股票i,我们得出的条件日订单失衡量如下:
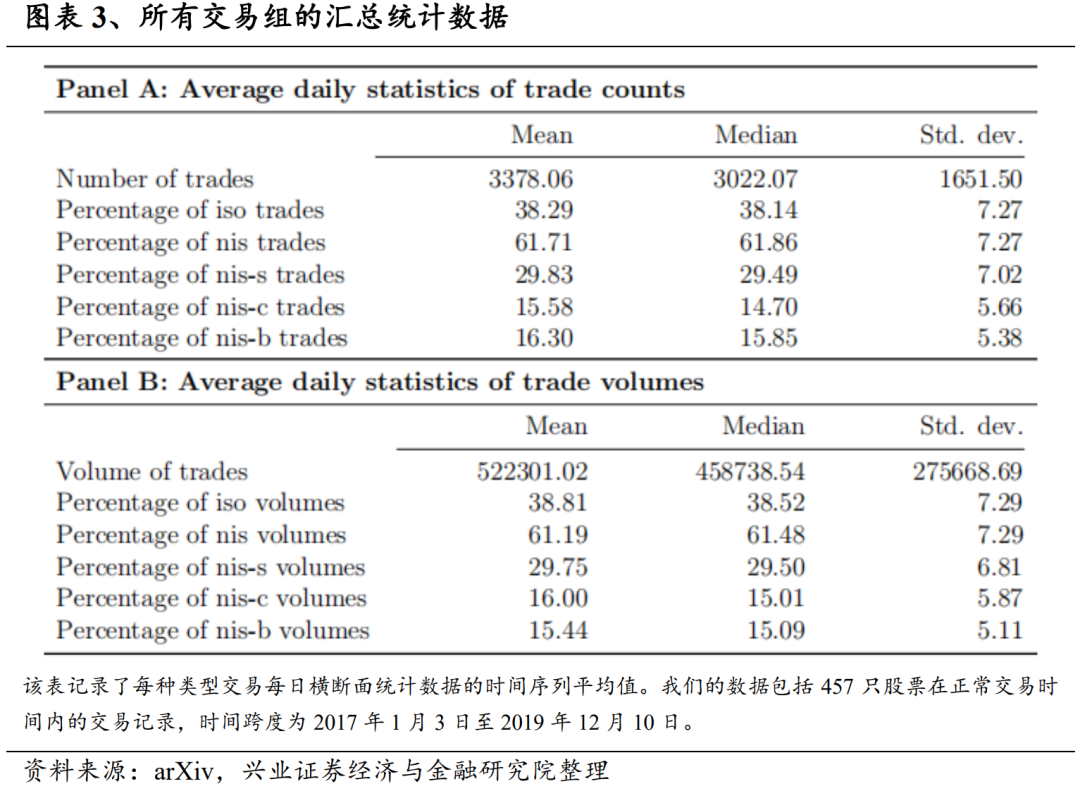
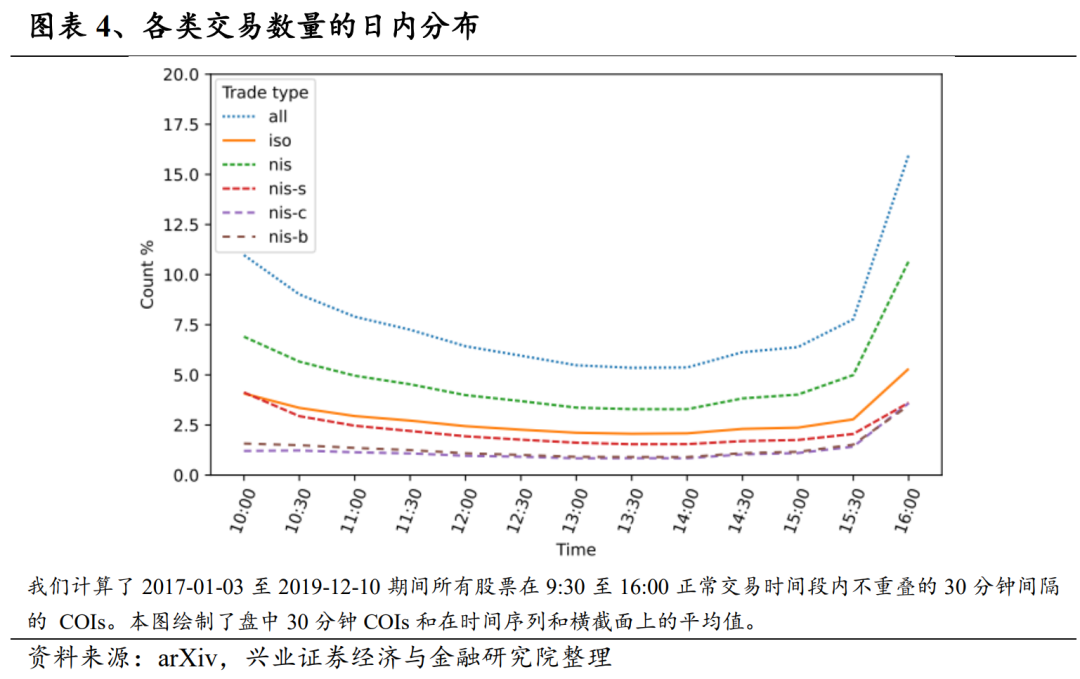
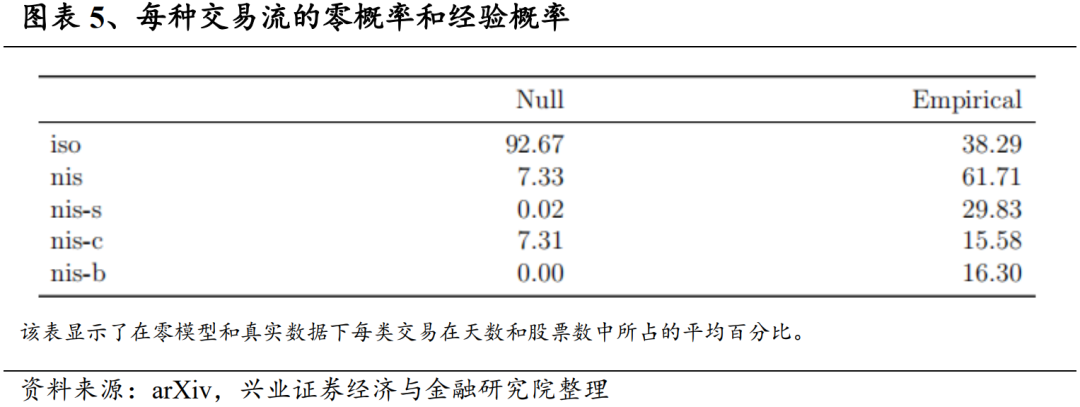
在本节中,我们将简要介绍实证研究中使用的数据。通过探索性分析,我们发现了交易共现的显著模式。此外,我们还发现,分解后的交易流订单失衡彼此之间存在弱相关性,这表明我们提出的交易分解是有意义的。我们的研究基于2017年1月3日至2019年12月10日期间的457只美国股票。所选股票是标准普尔(S&P)500指数中的公司,这些公司在整个样本期间都有订单数据和价格数据。我们从LOBSTER数据库(Huang和Polak(2011))中获取限价订单簿数据,该数据库提供了在纳斯达克交易所交易的所有股票限价订单的详细情况,包括限价订单的提交、取消和已执行交易,且所有记录以时间为索引,精度可达纳秒。对于每个交易日的每只股票记录包含限价订单事件的时间戳、事件类型(提交/取消/执行)、方向(买入/卖出)、大小和价格。通过过滤限价订单执行并逆转其方向,我们就能推断出买方和卖方发起的交易,例如,执行限价买入指令意味着市场发出“卖出指令/适销限价卖出指令”。我们注意到大量市场订单会同时消耗多个现有限价订单,鉴于LOBSTER的高时间分辨率,我们假设不同的交易不可能有完全相同的时间戳,从而合并订单推断出具有相同时间戳的交易。建立交易数据集后,我们为每笔交易贴上相应类型的标签。图表3列出了不同类型交易的数据摘要,选择的共现领域大小为500微秒(δ = 500µs)。面板A显示了原始数据的描述性统计,其中每个数字都是通过计算每日时间序列的平均,然后考虑所有股票的横截面平均值、中位数或标准差。平均值而言,隔离交易占交易总数的38.29%,而大多数交易都是属于三种定义(nis-s、nis-c、nis-b)中的非隔离交易。约一半的非隔离交易(占全部交易的29.83%)是非自我隔离交易(nis-s),非交叉隔离交易(nis-c)和非两者隔离交易(nis-b)的比例相似,平均值分别为15.58%和16.30%。交易数量的标准差较大,这表明该群体具有异质性。面板B显示了不同组别交易量的百分比,其与A组报告百分比非常相似。有鉴于此,将交易次数作为衡量流动性的指标是合理的。图表4强调了在交易日开始和结束时交易活动较高的经验事实,绘制了交易的日内分布,揭示了不同交易类型略有不同的时间行为。图中显示了每半小时各类交易的数量,Y 轴表示占总交易量的百分比。我们发现所有类型的交易都在最后半小时内急剧增加。值得注意的是,经过分解后,隔离交易的流动比非隔离交易的流动更平滑,在最后半小时的爬升中斜率较低。通过进一步分离非隔离交易的子类型,我们发现非自我隔离交易(nis-s)在交易日开始的贡献更大,而其他两类交易在交易日结束外的时段都是平缓的。有了订单数据,我们首先要回答以下基本问题:交易真的同时发生?还是它们的到达只是随机的、相互独立的?我们的交易流分解是否捕捉到了信号?在这一小节,我们将在完全随机订单到达的假设条件下建立一个空模型,通过比较零模型下的理论共现概率(Donges等人(2016))和从数据中得出的经验值,我们证实股票交易之间存在0.5毫秒级别的共现,支持了整体交易量具有很强的跨资产互动成分的观点。从经济学角度来看,这也许是意料之中的,因为如今市场上存在大量的指数套利交易者,他们同时进行指数ETF与一篮子成分股的交易。图表5展示了按时间和股票平均的空概率和经验日概率。考虑到极小的邻域大小(δ = 500µs),如果没有共现,92.67%的交易应该是被隔离的,然而市场上只有38.29%的交易是隔离交易。总之,有经验证据表明,交易共同发生的概念捕捉到了信号,这就促使我们对分解交易流并分别进行研究。
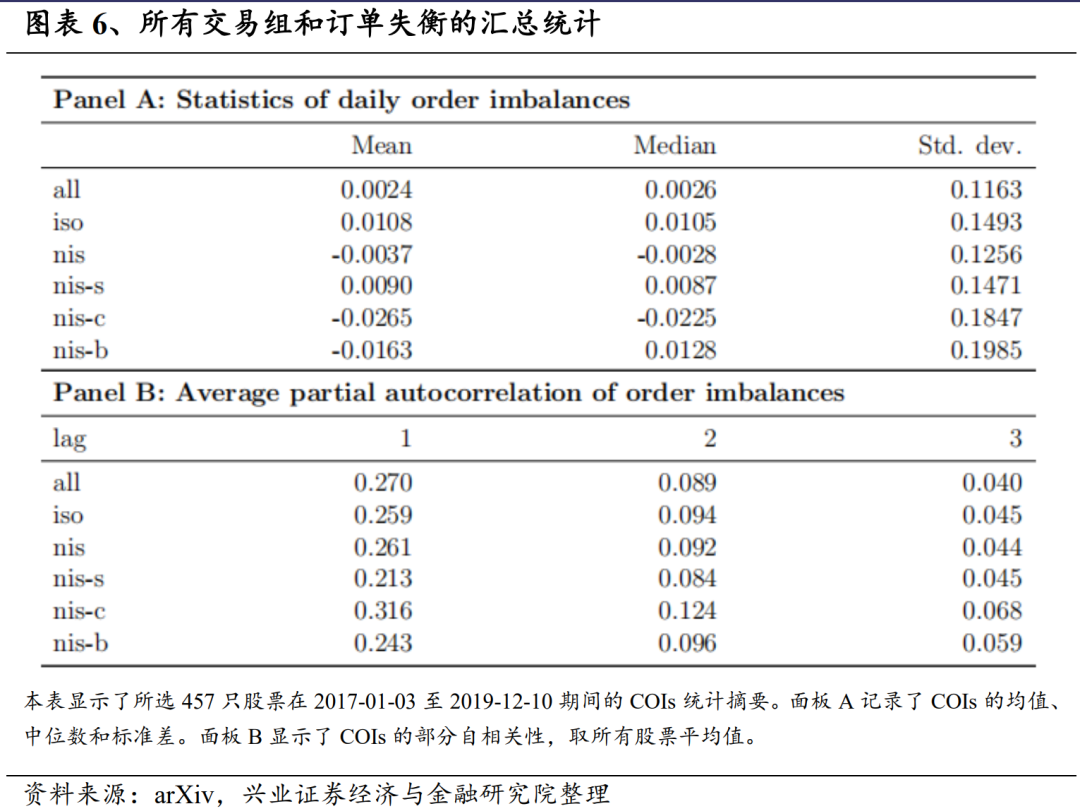
根据共现类型标记的交易,我们计算了每日订单失衡情况,并在图表6中报告了描述性统计数据。面板A记录了每类订单失衡的平均时间和股票。总体而言,平均无条件订单失衡为正值。在分解后,隔离和非自我隔离的订单失衡往往为正,其均值和方差均高于无条件订单失衡。与此相反,非交叉隔离和非两者隔离失衡的均值为负,但方差更大。因此,我们的研究本质上是以交易共现作为设定条件来构建具有不同行为的特征。然而,标准差远大于平均值,因此从统计学角度看,平均值与零并无显著差异。因此,均值只能作为潜在信号的一个非常微弱的指示。
面板B显示了各类订单失衡的平均偏自相关性。可以看出,所有订单失衡都是正的自相关。COIs滞后1期的自相关性很大。在条件失衡中,非交叉隔离的订单失衡与市场上其他股票的交易密切相关,其自相关性相对较高。相比之下,非自我隔离交易订单失衡的自相关性相对较低。随着滞后期的增加,这些偏自相关性急剧下降。
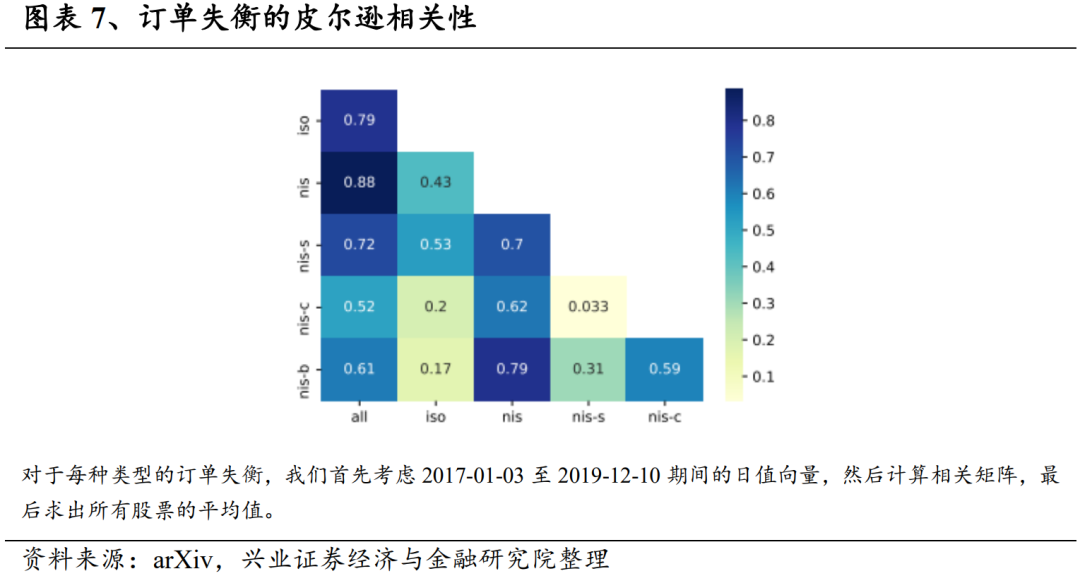
图表7展示了在δ=500微秒下COIs的皮尔逊相关性(所有股票的平均值)。所有类型的订单失衡都相互正相关,但强弱不同,可能相当低。无条件订单失衡是一个例外,它与其他所有类型的订单失衡都有很强的相关性。隔离失衡与非隔离失衡及其子类型之间的相关性很低。
正如预期的那样,隔离和非隔离条件会产生不同的特征。此外,通过分解非隔离交易得到的三个订单失衡与非隔离订单失衡的总和也有很强的相关性,但相互之间的相关性较弱。更详细地探讨它们之间的关系后,我们发现来源于未与市场上其他股票共同交易的非自我隔离交易的订单失衡与隔离订单失衡的相关性相对更高。相比之下,与市场联系更紧密的非交叉隔离交易和非两者隔离交易的订单失衡与隔离订单失衡的相关性较低。因此,我们确信分解后的订单失衡是可区分的特征,所有成对相关性都小于0.6,并且它们可以揭示股票市场的结构特性,而这些特性是无法通过观察总订单流量推断出的。
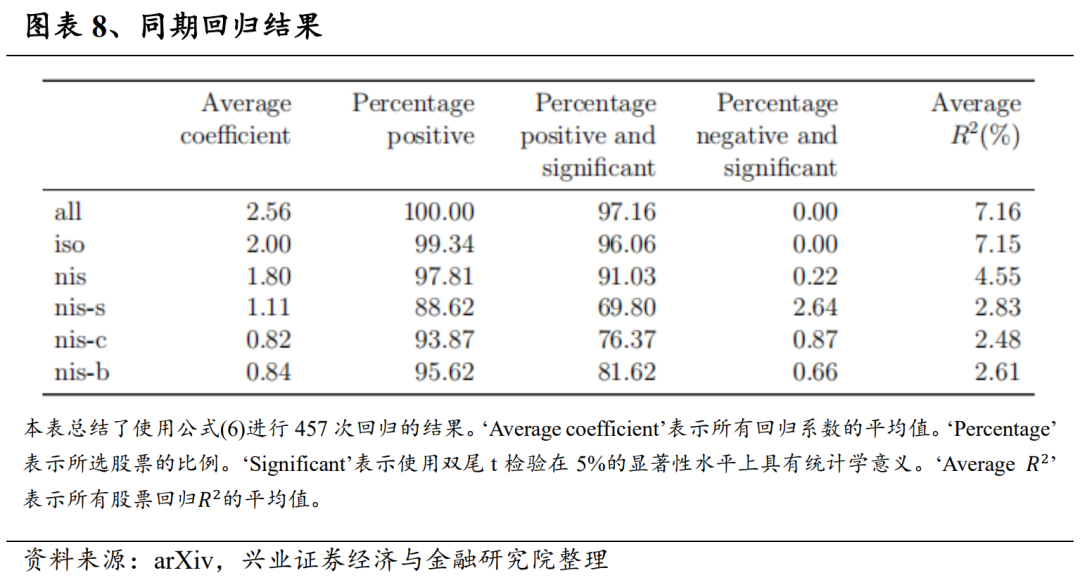
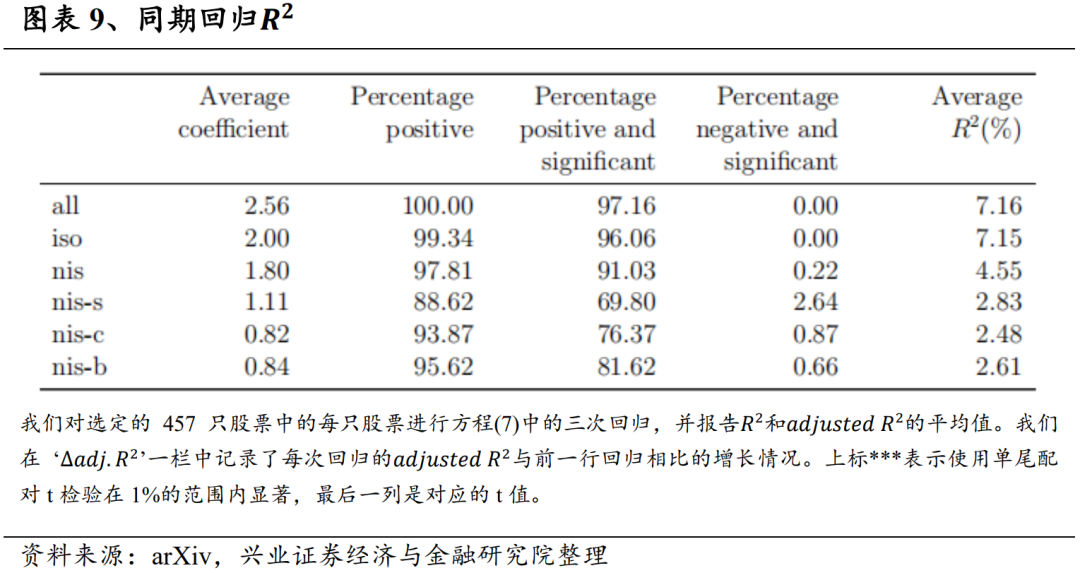
重点关注由同期收益率回归所解释的方差百分比,我们发现以所有交易计算的“all”组COI产生的R^2最高为7.16%。对交易流进行分解后,“iso”组COI虽然只计算了38.29%的交易,但其解释的方差与“all”组COI相当。与 “all”组或“iso”组COI相比,用“nis”组COI对回报率进行回归所得到的R^2较低。因此价格影响并不与数量成正比,而似乎是由交易类型驱动的。这表明,与市场上其他交易有明显共现关系的交易所产生的价格压力是不均匀的且值得单独研究。
除了研究个体条件订单不平衡对收益的显著影响外,我们还对分解总订单失衡所获得的额外信息感兴趣。为此,我们拟合了以下三个回归方法:
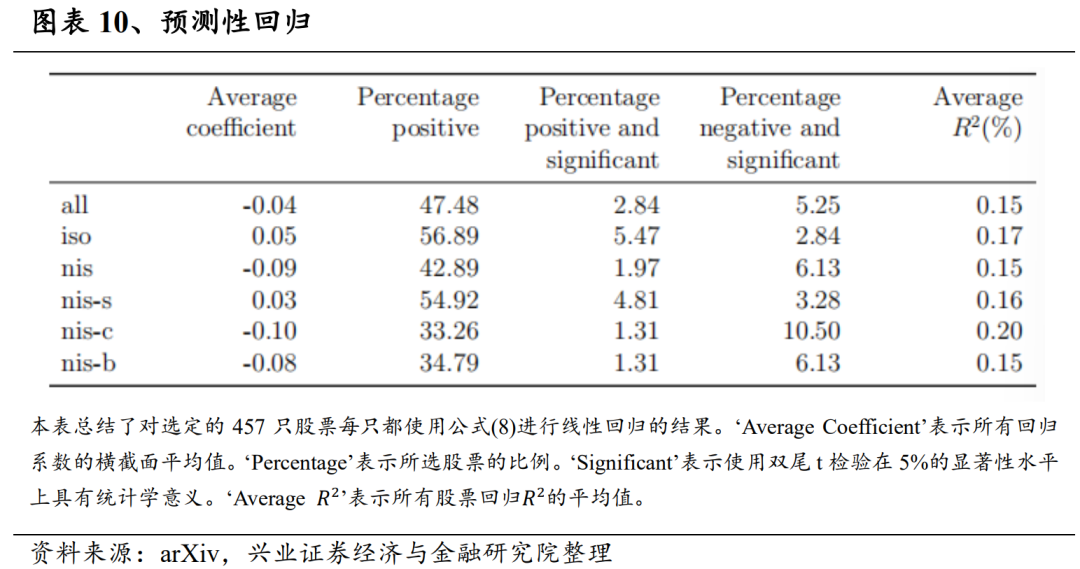
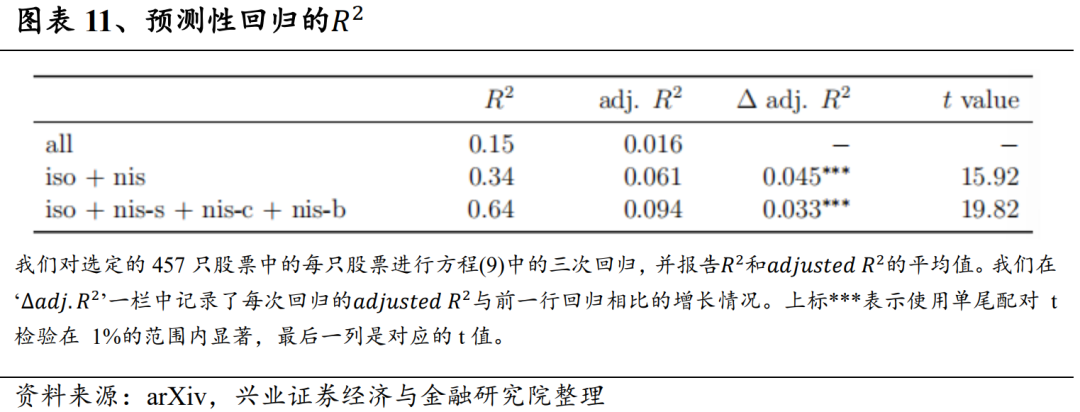
结合订单失衡的同期效应,研究其预测能力也很重要。在本节中,我们发现iso和nis-s订单失衡与未来收益率呈正相关,而nis、nis-c和nis-b的COIs与未来收益率呈负相关。此外,我们还发现,分解交易流以及同时使用多个COIs包含了预测次日回报的信号。我们利用回归和投资组合排序方法进行举证。
我们重复上一节的回归分析思路,探讨COIs与前一天市场超额收益之间的关系。首先,我们将未来收益率与当前COIs分别进行回归,模型为:
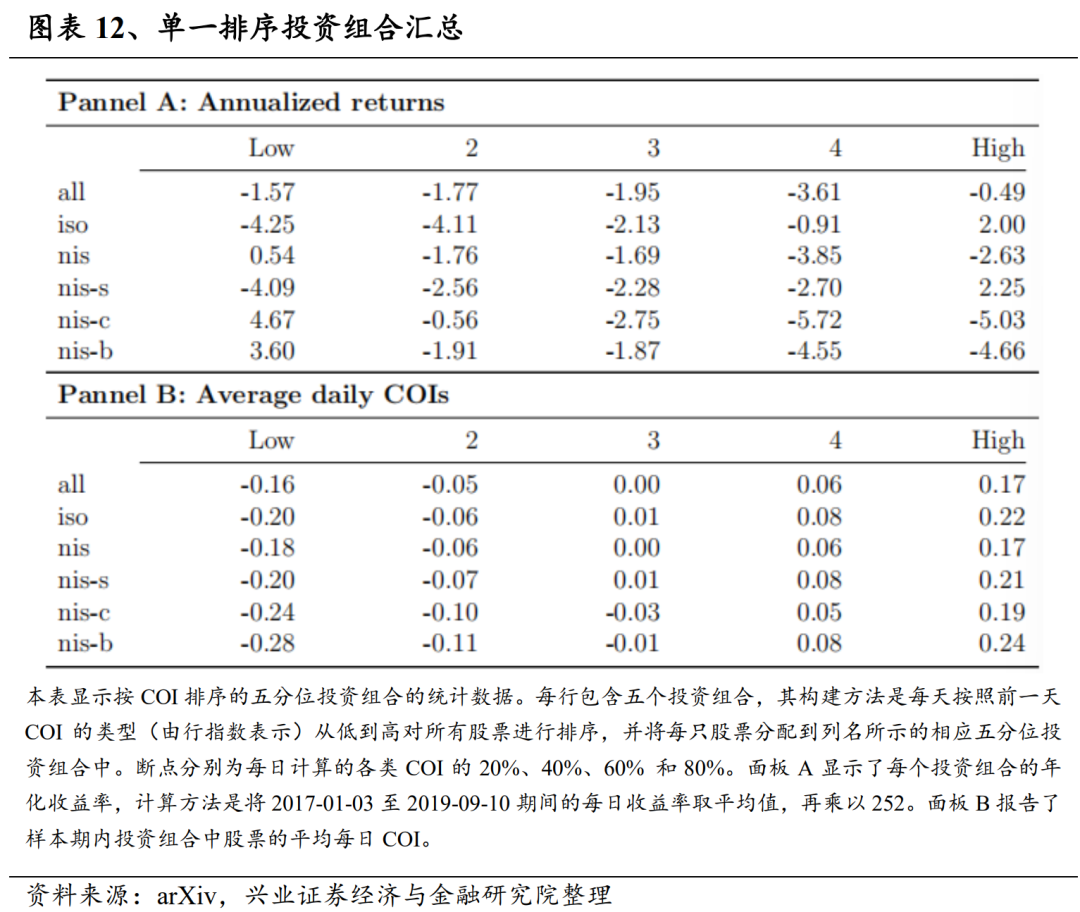
为了证实我们对未来回报与不同类型COI之间正负关系的研究结果,我们采用了投资组合排序法(Cattaneo等人(2020)、Fama和French(1993))将订单失衡转化为投资组合。对于每类COI,我们根据其失衡值从低到高将股票分为5 个五分位组合。考虑到多重特征,我们进一步为每对COIs创建5×5双重排序组合。失衡排序的投资组合权重相同,只持有股票的多头头寸,投资组合的日收益率按所有股票的平均收益率计算。在2017-01-03至2019-12-10的整个样本期内,对失衡排序投资组合进行的回溯测试强化了这一发现,即 iso 和nis-s失衡是动量信号,而nis、nis-c和nis-b失衡是反转信号,它们对未来回报的影响不同。在2017年1月3日至2019年12月10日的整个样本期间,对不平衡排序的投资组合进行的回溯测试强化了这一发现:iso和nis-s失衡是动量信号,而nis、nis-c和nis-b失衡是反转信号,它们对未来回报的影响各不相同。
6.2.1、单一排序投资组合
图表12面板A记录了单一排序投资组合的年化收益率。我们注意到,在第一行中,无条件失衡排序投资组合的收益率为负值,且在五分位数上波动,这证实了无条件订单失衡与未来收益率之间没有明显的线性关系。然而,在分解交易流后,我们发现随着等序失衡的增加,回报率的增长是单调的,这加强了等序失衡与未来回报率的正相关性。同样,nis-s也呈上升趋势,这也是正相关的表现。与此相反,我们观察到其他类型COIs的平均回报率在下降,这与我们的时间序列回归结果一致,证实了负相关关系。
面板B显示了每个投资组合中股票的日平均COIs。COIs是有符号的,表示为“Low”和“High”投资组合对应于符号相反的强信号。我们观察到,所有信号强度的分布大致对称,且以0为中心。在每一行中,不存在由平均COI值无差别的股票组成的五分位投资组合。然而,五等分法的投资组合收益既不对称,也不单调(iso除外)。通过比较面板A各行的回报率,我们发现最大正回报率的幅度总是小于最小负回报率的绝对值。因此,我们推测COIs对未来回报的正负影响是不对称的,负值影响更大。
此外,就对未来回报的负面影响而言,COIs的最大值并不会导致次日的最大跌幅。例如,“iso”COI 的最低五分位数和第二五分位数投资组合的回报率相似,而对于“nis”COI 的投资组合,第四五分位数投资组合的平均回报率最低,为-3.85%,而最高的五分位数投资组合的回报率则上升至-2.63%。对于上述现象,我们解释为极端不平衡会导致次日出现强劲反转,因为一些投资者的目标是保持稳定的风险敞口水平。
6.2.2、双排序投资组合
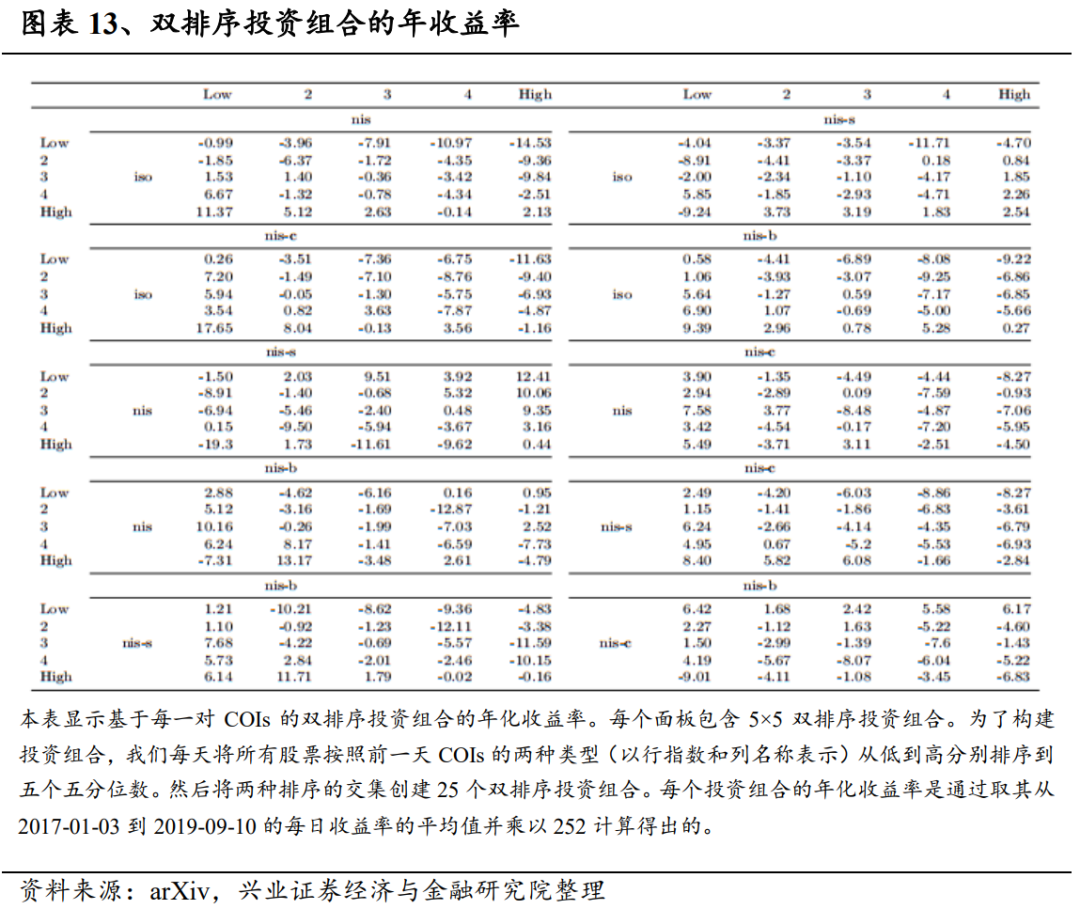
为了进一步研究COIs之间的相互作用,我们通过对分解交易流的每一对失衡信号进行独立的双重排序来建立投资组合。图表13列出所有投资组合的年化收益率,其中每个区块包含25个投资组合,根据行名和列名所示的一对信号进行排序。
在每列等值区块中,平均收益率随着隔离交易的低COIs值到高COIs值依次上升。与此相反,使用等COI进行控制时,收益通常会随着非隔离COI值变高而下降。对最强信号进行双重排序,可在区块的右上角和左下角获得最高和最低收益。最强回报的幅度为11.37%和-14.53%,与单个信号排序的最强回报幅度相比也有所提高。除了nis-s—nis-b,对每对动量和反转COI特征进行双重排序时,都会出现相同的模式和改进。然而与未来回报率具有相同关系的成对COIs的模式并不明显。例如,从等isonis-s排序的区块来看,我们无法观察到沿行和沿列的单调模式。因此,我们推测,动量信号和反转信号带有不同的信息,同时纳入这两种信号可提高预测能力。
如前几节所述,有证据表明条件订单失衡包含解释和预测个股收益的信号。在本节中,我们利用排序形成多空投资组合,从而利用其经济价值。我们基于失衡的交易策略产生了明显的利润和显著的异常回报。高额的交易利润也为分解后的交易流的COIs所具有的预测能力提供了重要证据。
我们根据不平衡排序的五分位投资组合设计实用的交易策略。在每个交易日的上午9:30时,我们买入第一个(或最后一个)五分位数组合,并卖空最后一个(或第一个)五分位数组合,以获得相同数量的动量(或反转)信号,从而实现自我平衡。每天,我们在下午16:00关闭所有仓位,以避免隔夜效应。总体而言,每日收益率是多头和空头不平衡排序投资组合收益率之间的差额。
为了评估盈利能力,我们比较了投资组合的年化收益率以及年化夏普比率(Sharpe(1994)),定义为:
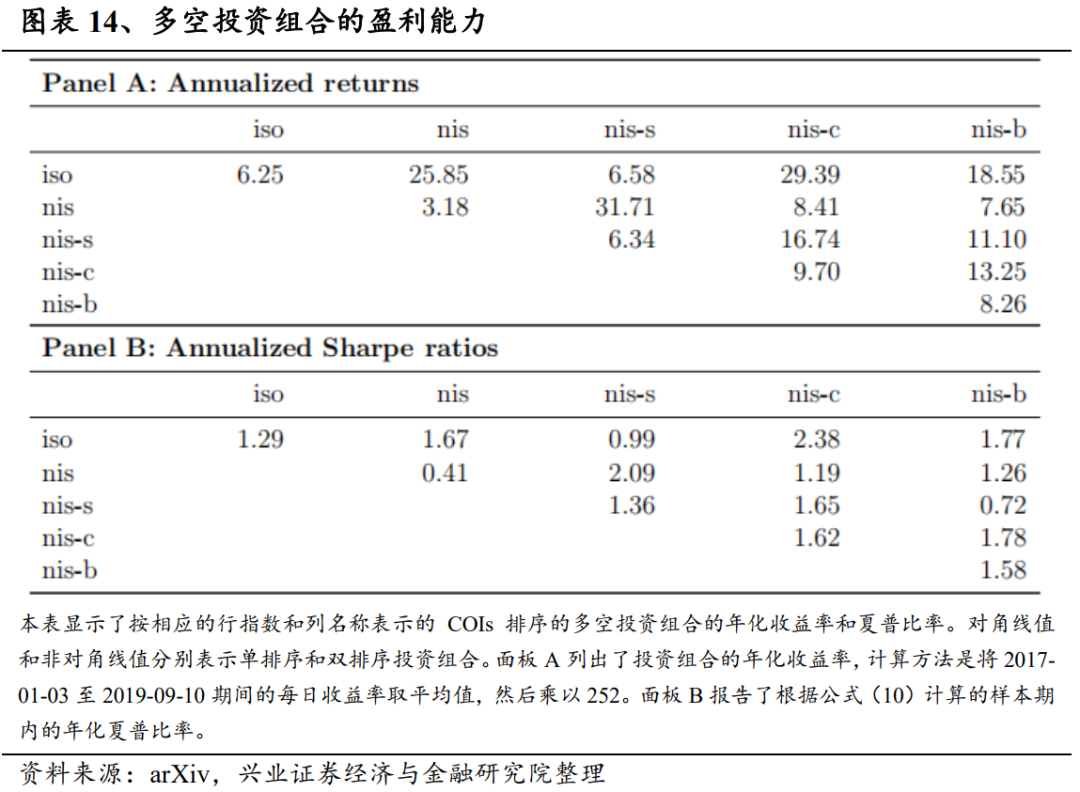
我们构建了多空投资组合,并在图表14中报告了其盈利能力指标。面板 A 显示了年化收益率,行名和列名分别表示了基于COIs的单排序和双排序投资组合的对角线和非对角线数值。我们发现,纳入多个COIs可以提高投资组合的收益,这也证明了交易流分解技术可以创建有利可图的COI信号。例如,“iso—nis”双排序对应的多空策略收益率为25.85%,比简单地分别对“iso”和“nis”COI排序高出19.60%和22.67%。通过对“nis-s”和“nis”COI进行双重排序,最高年化收益率达到 31.71%。一般来说,如果将对角线以外的值与行列上相应的对角线值进行比较,我们会发现所有10个双重排序的多空组合的收益率至少高于其中一个单一排序的基准值,而且10个组合中有9个组合的收益率高于两个基准值。
面板B中的夏普比率证实了我们对COI信号经济价值的发现。经风险调整后,我们的交易策略仍然有利可图,双重排序优于单一信号交易。以“iso”和“nis-c”排序的投资组合的夏普比率最高,达到2.38,其次是以“nis-snis”排序的投资组合的夏普比率为2.09。此外,80%的非对角线值至少高于一个相应的对角线值,50%的非对角线值高于两个对角线值。因此,有迹象表明,对于投资者来说,在做出交易决策时纳入多种类型的COIs是有经济效益的。
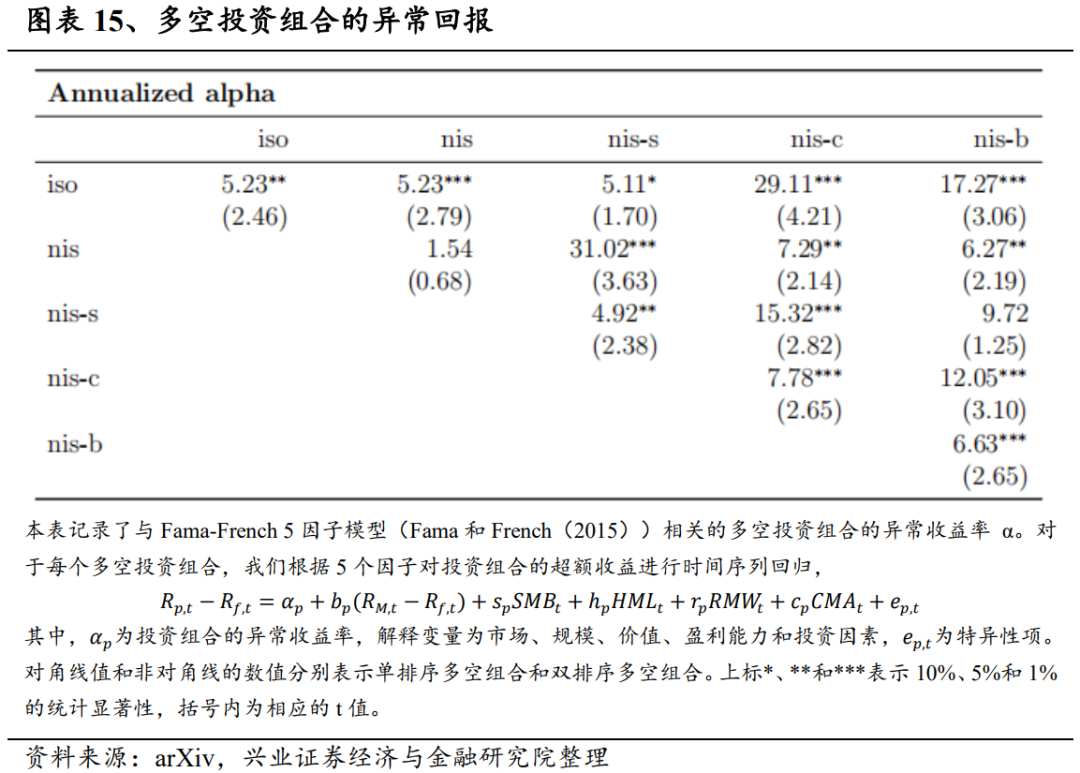
从资产定价的角度来看,COIs是异常收益的独特且重要的来源。我们将多空投资组合的超额收益与Fama-French五因子(Fama和French(2015))进行回归,并在图表15中显示了它们的α值。除了基于“nis”COI的单一排序外,所有投资组合都产生了统计意义上的显著异常回报,这证明利润无法用普通风险因子来解释。
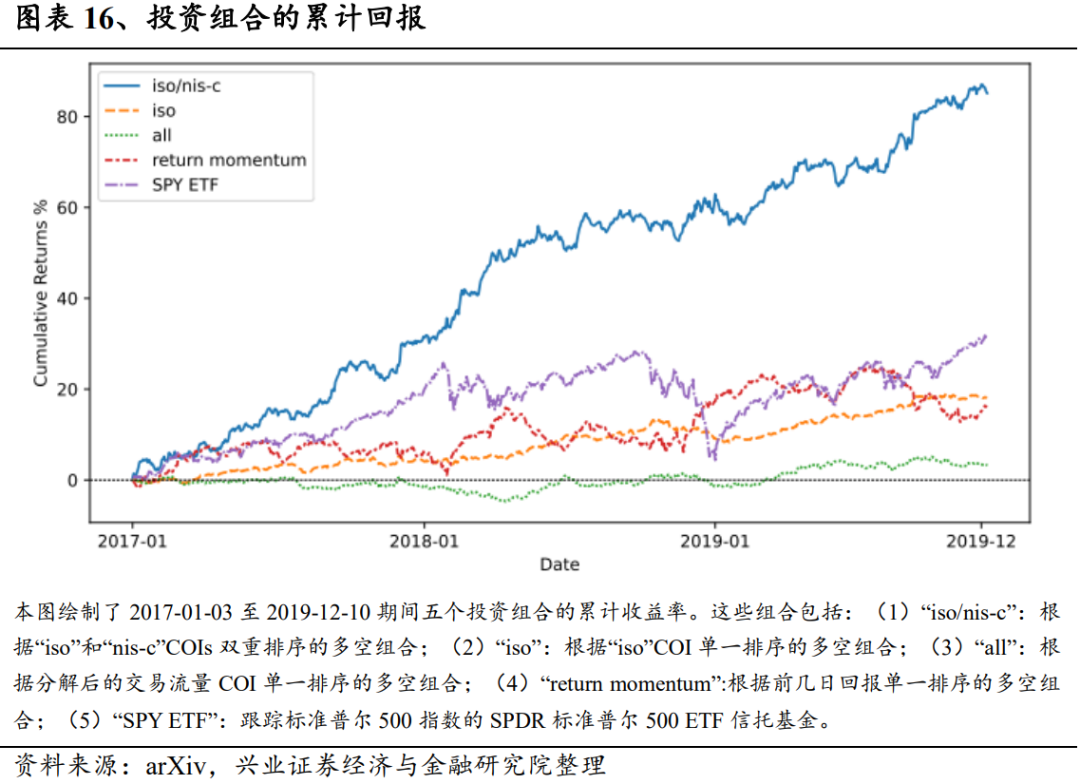
我们还将我们的策略与三个基准投资组合进行了比较。第一,我们构建了一个包含“all”COI的多空投资组合,以评估分解交易流的经济价值。第二,我们根据前几天的收益率构建了另一个基准多空投资组合。由于COIs与同期收益率存在显著相关性,因此有必要证明价格并不能完全揭示盈利能力。第三,我们选择SPY作为可交易市场组合,以整体市场表现为基准。在基于COI的策略中,我们选择“iso”COI的单排序组合以及“iso”和“nis-c”COI的双排序组合作为代表。图表16显示了选定的基于COI的多空投资组合和基准的累计回报。在测试期间,我们发现使用分解交易流的COIs没有获得任何利润。回报动量多空组合和SPY的夏普比率分别为0.45和0.73。“iso”单一排序组合的年化收益率与收益动量相似,但波动性更小,夏普比率达到1.29。显然,双排序投资组合的回报率和夏普比率都优于其他所有投资组合。
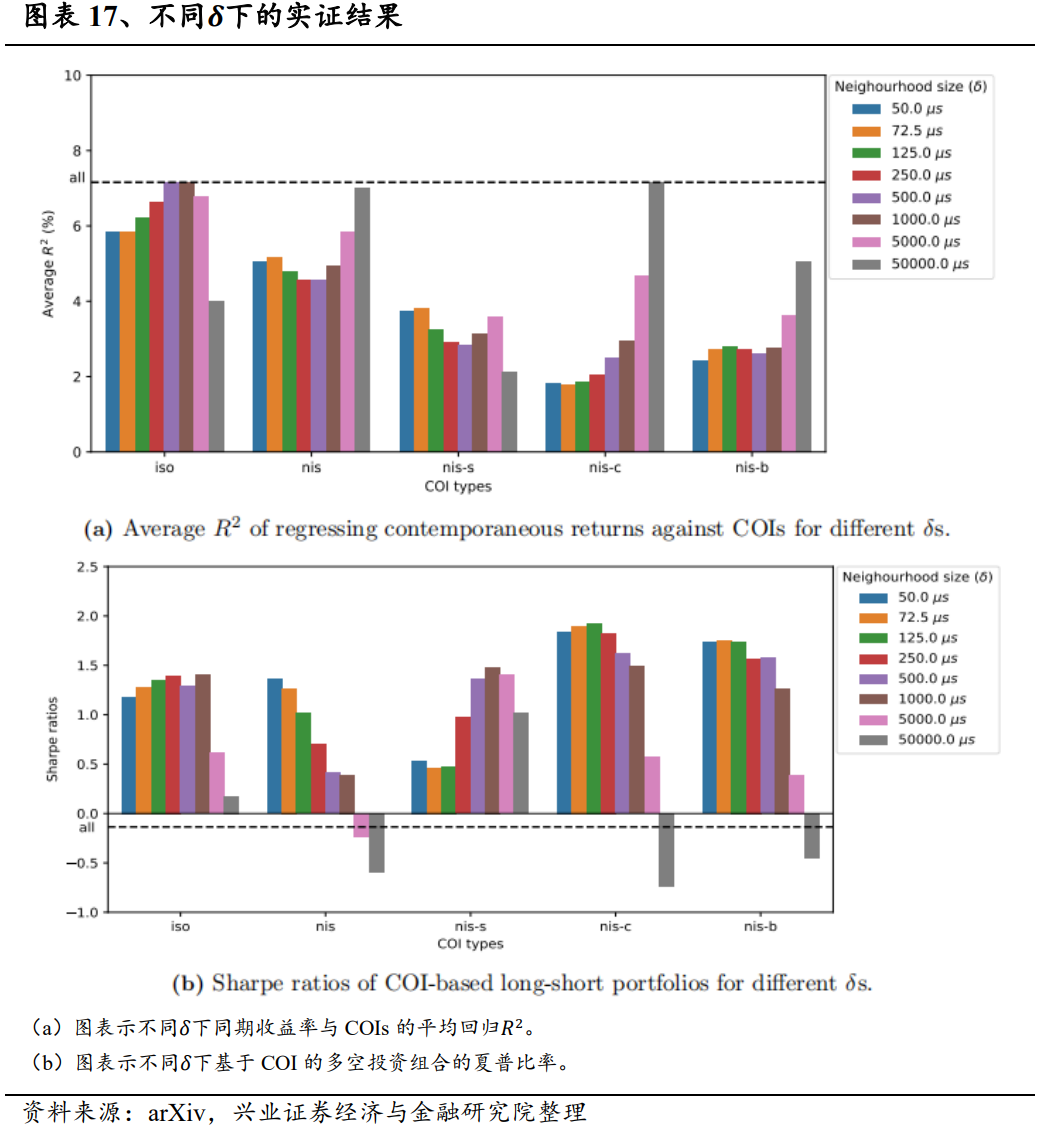
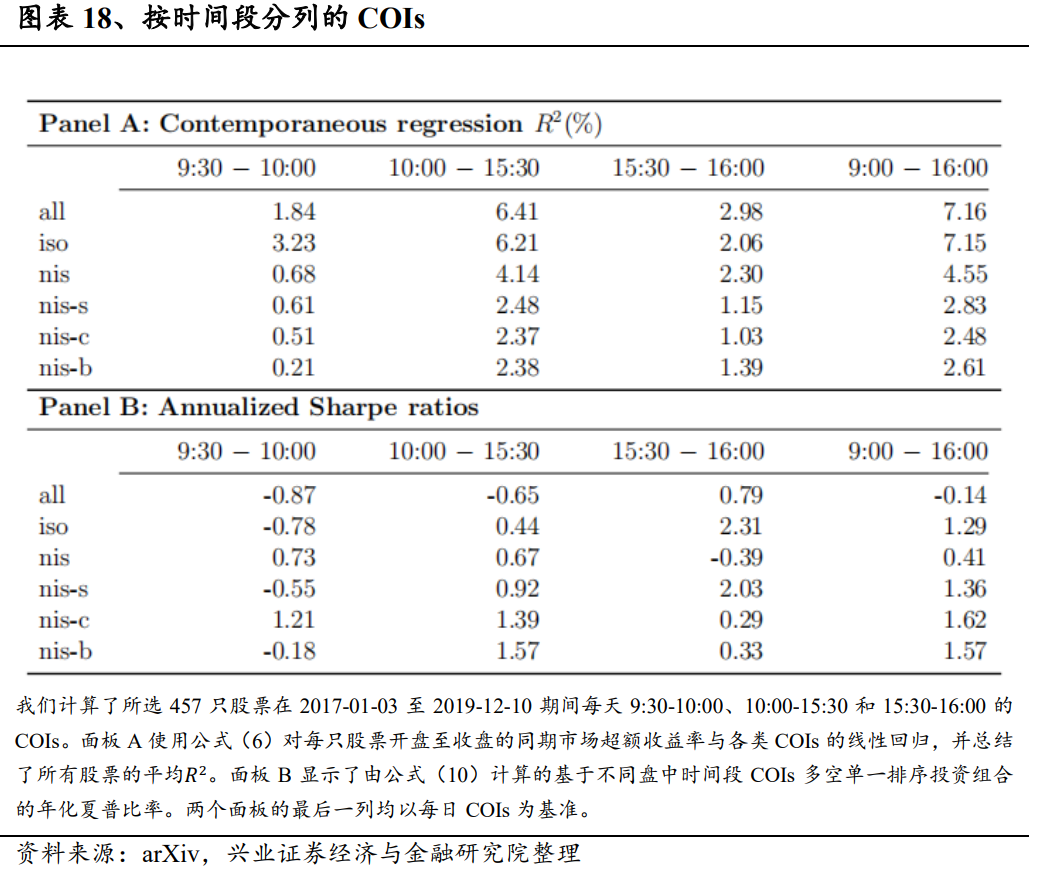
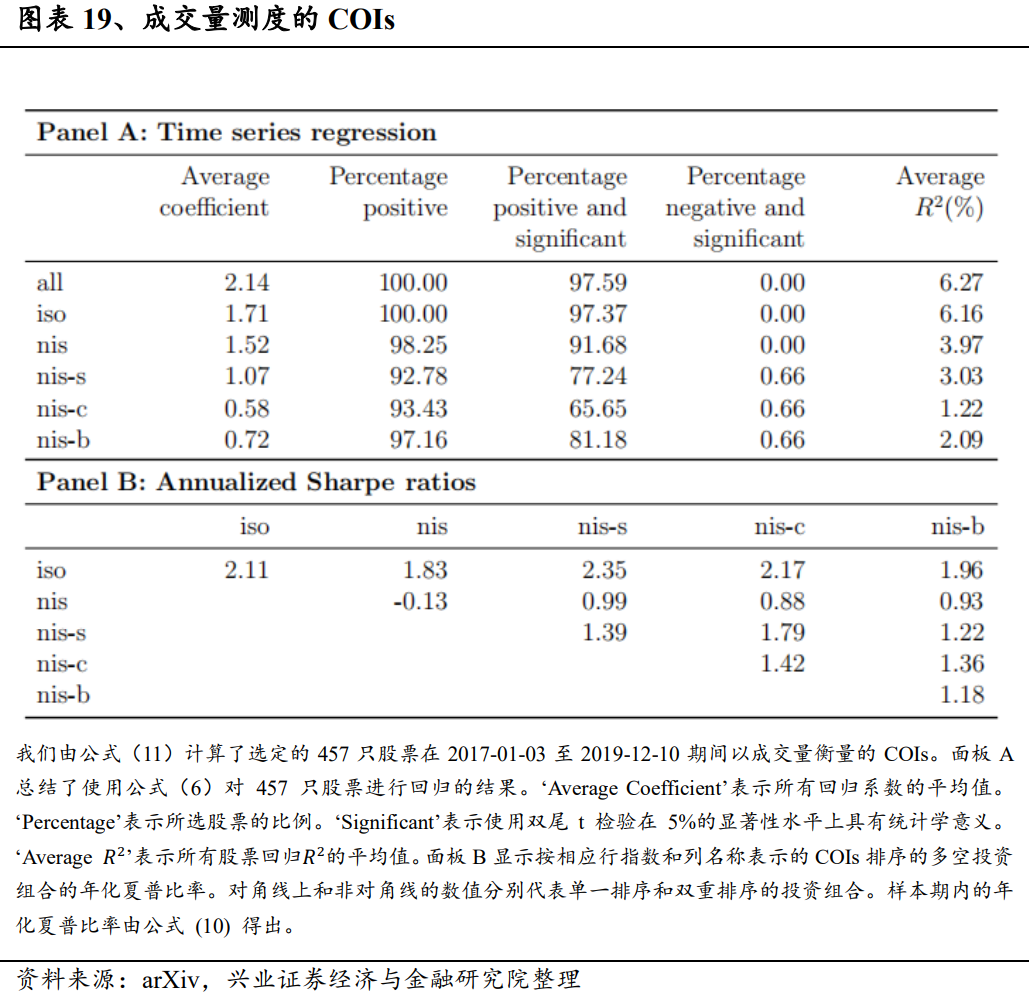
在本节中,我们将简要评述交易共现的识别的稳健性以及条件订单失衡的构建。更多详情见附录。交易共现的定义和单个交易的分类取决于邻域大小δ的选择。当考虑到δ=0的极端情况时,所有交易都是相互隔离的。随着δ的逐渐增大,隔离交易会变成非隔离交易的一个子类型。同时,非自我隔离交易和非交叉隔离交易都只能变成非两者隔离交易。最终,当δ足够大时,所有交易都是非隔离的;具体地说,所有交易都变成了非两者隔离的。因此,随着δ值的增大,隔离交易的数量会减少,非隔离交易和非两者隔离交易的数量会单调增加。因此,非自我隔离和非交叉隔离交易的数量最初会增加,达到各自的最大值后,它们开始减少。我们对附录A中的8个δ值重复进行了分析。对于较小的邻域规模,同期影响和预测能力的模式是稳健的。然而,当δ达到50毫秒时,交易共现作为过滤器的性能就会下降。此外,不同类型的COIs在不同的值下都能达到最佳效果,这表明该方法在结合来自多个δ值的信号方面具有潜在优势。不同盘中时段的交易活动对价格有不同的影响。我们注意到,交易活动在每个交易日的第一个小时和最后半个小时更为密集。最近的一些研究,如Cont、Cucuringu和Zhang(2021)在计算失衡时排除了这些波动时段以确保稳健性,而其他研究(Chu和Qiu(2021))则特别关注这些半小时时段的失衡。考虑到日内时间效应,我们分别研究了三个时间段内的COIs,即9:30-10:00、10:00-15:30和15.30-16:00,并在附录B中记录了我们的研究结果。我们关于同期回报与失衡关系的研究结果在每个时期都成立。此外,我们还发现分解后的交易流的预测能力来自不同的时间段。最后一小时的“iso”和“nis-s”COIs有助于预测未来收益。另一方面,“nis-c”COI 的预测能力来自最后半小时以外的时段。此外,对于“nis-b”交易,只有10:00-15:30的COI才有助于预测次日开盘至收盘的市场超额收益。除了纳入交易数量外,人们通常还将订单失衡定义为买方和卖方发起的交易量之间的标准化差异。我们研究了个股收益与交易量订单失衡之间的关系,并分析了相应的交易策略。更多详情见附录 C。在交易量衡量标准下,我们的研究结果是稳健的。我们观察到与计数COIs相同的模式,但注意到在所有交易类型中,与交易量失衡相关的同期回归R2比与计数失衡相关的回归R2低约1%。这一发现与之前的研究(Chan和Lakonishok(1995)、Chordia和Subrahmanyam(2004))一致,这些研究提供的证据表明,交易数量能更好地捕捉机构为优化执行而拆分订单所带来的价格压力。
在本文中,我们提出了 "交易共现 "的概念,它将时间上相互接近的交易联系起来,从而能够在细粒度上研究股票交易之间的相互作用。在与其他交易共同发生的条件下,我们将每笔交易分为五组。我们计算每种类型的分解交易流(COI),并研究其对个股回报的同期影响、预测能力以及其经济价值。我们的实证结果表明,分解交易流对价格的影响各不相同。“iso”交易流的COI就能解释当日收益率的变化,与使用未分解的总交易流的COI的解释能力相当,而加入交易流的COIs则进一步提高了解释能力。就可预测性而言,我们观察到,平均而言,未来回报与“iso”和“nis-s”的COIs呈正相关,而与“nis”、“nis-c”和“nis-b”的COIs呈负相关。此外,交易流分解具有显著的经济价值,根据以往COIs的发展方向构建多空投资组合会明显提高交易策略的盈利能力。最后,我们提出了两个未来发展方向,特别是考虑到我们目前在数据可用性和计算能力方面的局限性。首先,我们通过经验证明了根据交易与其他交易的共同发生率来分解交易的重要性,但我们无法确定是谁发起了某些类型的交易。利用私人数据集区分不同类型的交易者(Tumminello等人(2012),Cont、Cucuringu、Glukhov等人(2021)),并发现交易互动背后的机制,这将是一个有趣的研究方向。例如,检测机构等知情交易者是否会成功隐藏其交易目的,从而导致其交易极有可能与其他交易隔离,这将是一个令人感兴趣的问题。如果能识别出高频交易者,就值得应用共现分析来了解高频交易者如何对其他市场参与者的交易活动做出反应。其次,为了实现数据缩减的目的,我们只研究限价订单的执行情况,而非所有限价订单簿事件。过去的研究发现,限价订单的提交和取消也会对价格产生影响。将我们的想法扩展到限价订单的共同发生,并深入研究订单流失衡(Eisler、Bouchaud和Kockelkoren(2012),Cont、Kukanov和Stoikov(2014),Xu、Gould和Howison(2018),Cont、Cucuringu和Zhang(2021))可能会很有趣,这与我们的COIs类似。
我们研究了不同盘中时间间隔的COIs。首先,我们将当时开盘到收盘的市场准入回报与每个COI分别进行回归,以评估它们对当日价格变化的影响。图表18面板A列出了所有此类回归的R2。剔除最开始半个小时和最后半个小时的交易并不会明显改变我们发现的失衡与收益之间的关系。无论在哪个时段,只用“iso”交易得出的COIs都足以解释与使用所有交易时相近的方差。请注意,尤其是在第一小时,价格影响主要来自于隔离交易。其次,我们通过构建单一序列的多空组合对每个COI进行交易,并在面板B中显示年化夏普比率。我们可以合理地预期,在正常交易期末期的交易活动更有助于预测COI。我们观察到,最后一小时的“iso”和“nis-s”COIs信号导致夏普比率分别上升1.03和0.67,显著提高了投资组合的利润。相反,最后半小时的非交叉隔离COI并不是预测未来收益的良好信号。就非交叉隔离交易(nis-b)而言,只有在波动较小的交易时段,COI才能预测未来收益。
风险提示:模型结果基于历史数据的测算,在市场环境转变时模型存在失效的风险。

注:文中报告节选自兴业证券经济与金融研究院已公开发布研究报告,具体报告内容及相关风险提示等详见完整版报告。
证券研究报告:《西学东渐--海外文献推荐系列[文]之一百五十九》
对外发布时间:2023年11月23日
报告发布机构:兴业证券股份有限公司(已获中国[章]证监会许可的证券投资咨询业务资格)
----------------------[来]----------------
分析师:郑兆磊
SAC执业证书编号:S01905200800[自]06
E-mail: [email protected].[1]cn
----------------------[7]----------------
更多量化最新资讯和研究成果,欢迎关注我们的微[量]信公众平台(微信号:XYQuantResea[化]rch)!