【华安金工】基于残差因子分布预测的投资组合优化——“学海拾珠”系列之一百七十五
►主要观点
01
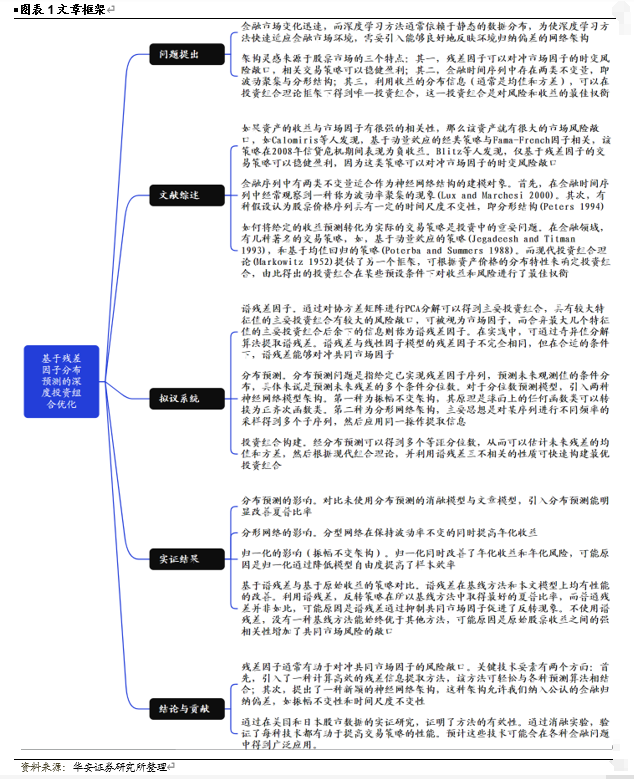
制定可盈利的交易策略是金融行业的核心问题。在过去的十年里,机器学习和深度学习技术在许多应用领域中取得了重大进展(Devlin et al. 2019; Graves, Mohamed, and Hinton 2013),这激发了投资者和金融机构开发机器学习辅助交易策略的热情(Wang et al. 2019; Choudhry and Garg 2008; Shah 2007)。然而,人们认为预测金融时间序列的本质是一项困难的任务(Krauss, Do, and Huck 2017)。尤其是众所周知的有效市场假说(Malkiel and Fama 1970)认为,由于市场动态变化迅速,没有任何一种交易策略可以永久盈利。在这一点上,金融市场与大多数机器学习/深度学习方法通常假设的静态环境有很大不同。
一般来说,深度学习方法快速适应给定环境的好方式是引入一种能够很好地反映环境归纳偏差的网络架构。此类架构最突出的例子包括用于图像数据的卷积神经网络CNNs (Krizhevsky, Sutskever, and Hinton 2012)和用于一般时间序列数据的长短期记忆网络LSTMs (Hochreiter and Schmidhuber 1997)。因此,一个自然而然的问题是,什么样的架构能有效处理金融时间序列。
许多关于股票收益的实证研究都是用因子模型来描述的(e.g., Fama and French 1992, 2015)。这些因子模型将股票i在时间t的收益率表示为K个因子加上一个残差项的线性组合:
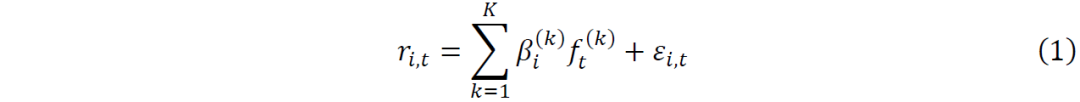
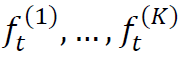 是股票i ∈ {1, ..., S}的共同因子,
是股票i ∈ {1, ..., S}的共同因子,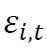 是对应于个股i的残差因子。因此,共同因子对应的是整个股票市场或行业的动态,而残差因子则传达了一些公司的特定信息。
是对应于个股i的残差因子。因此,共同因子对应的是整个股票市场或行业的动态,而残差因子则传达了一些公司的特定信息。消除市场效应和提取残差因子的一种自然方法是利用线性分解方法,如主成分分析(PCA)和因子分析(FA)。在训练基于深度学习的策略时,从观测数据中学习这种分解结构是较为困难的。一个可能的原因是,学习到的策略会偏向于使用市场因子的信息,因为市场因子的影响在许多股票中占主导地位(Pasini 2017)。因此,为了利用残差因子,在架构中明确实现类似分解的结构是合理的。
02
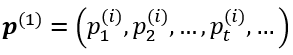 ,其中,
,其中, 是股票i在时刻t的价格。我们主要考虑股票的收益率,而非原始价格。股票i在时刻t的收益率定义为
是股票i在时刻t的价格。我们主要考虑股票的收益率,而非原始价格。股票i在时刻t的收益率定义为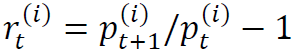 。
。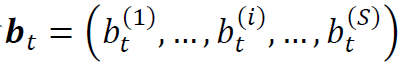 ,其中
,其中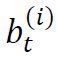 是股票i在时刻t的投资数量,满足
是股票i在时刻t的投资数量,满足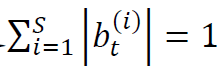 。投资组合
。投资组合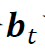 可以理解为一种特殊的交易策略,即
可以理解为一种特殊的交易策略,即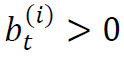 意味着投资者在时刻t对股票i持有数量为
意味着投资者在时刻t对股票i持有数量为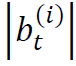 的多头头寸,而
的多头头寸,而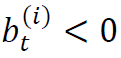 则意味着对该股票持有空头头寸。给定投资组合
则意味着对该股票持有空头头寸。给定投资组合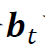 ,其在时刻t的总收益
,其在时刻t的总收益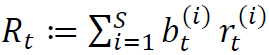 ,那么,给定个股收益的历史观测值,我们的任务就是确定能够最大化未来收益的
,那么,给定个股收益的历史观测值,我们的任务就是确定能够最大化未来收益的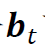 。
。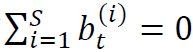 。
。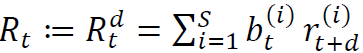 。
。根据现代投资组合理论(Markowitz 1952),投资者构建投资组合的目的是在特定的可接受风险水平下实现预期收益最大化。标准差通常用于量化风险或多变性,所谓多变性是指衡量股票年收益率偏离其长期历史均值的程度(Kintzel 2007)。
夏普比率(Sharpe 1994)是金融领域最常用的风险/收益衡量标准之一。它是指每单位波动所获得的超过无风险利率的平均收益。夏普比率的计算公式为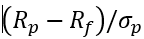 ,其中
,其中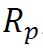 是投资组合的收益,
是投资组合的收益,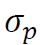 是投资组合超额收益的标准差,
是投资组合超额收益的标准差,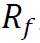 是无风险资产(如政府债券)的收益。对于零投资组合,我们可以省略
是无风险资产(如政府债券)的收益。对于零投资组合,我们可以省略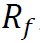 ,因为它不需要股权(Mitra 2009)。
,因为它不需要股权(Mitra 2009)。
在本文中,我们采用夏普比率作为投资组合构建问题的目标。由于我们不可能总是事先获得总风险的估计值,因此我们通常会考虑下一期夏普比率的序列最大化。一旦我们得到未来收益的均值向量和协方差矩阵的预测值,最优投资组合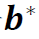 就可以求解为
就可以求解为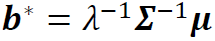 ,其中,λ是代表相对风险厌恶程度的预定义参数,Σ是估计的协方差矩阵,
,其中,λ是代表相对风险厌恶程度的预定义参数,Σ是估计的协方差矩阵,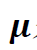 是估计的均值向量(Kan and Zhou 2007)。因此,预测均值和协方差对于构建风险厌恶的投资组合至关重要。
是估计的均值向量(Kan and Zhou 2007)。因此,预测均值和协方差对于构建风险厌恶的投资组合至关重要。
03
在本节中介绍我们所提出的系统的详细信息,如图表2所示。我们的系统由三部分组成。在第一部分(i)中,系统提取残差信息以对冲共同市场因子的影响。为此,我们在第3.1节中引入了谱残差,这是一种基于谱分解的新方法。在第二部分(ii)中,该系统使用基于神经网络的预测器来预测谱残差的未来分布。在第三部分(iii)中,利用预测的分布信息构建最优的投资组合。我们将在第3.2节中概述这些步骤。此外,我们还引入了一种新颖的网络架构,它结合了众所周知的金融归纳偏差,我们将在第3.3节中对此进行解释。
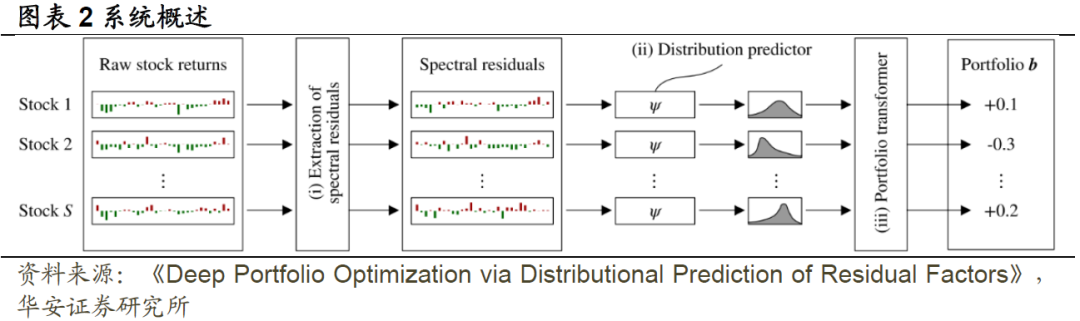
正如引言所述,本文的重点是开发基于残差因子的交易策略,其中残差因子是指在对冲共同市场因子后的剩余信息。本文引入了一种新的提取残差信息的方法,称之为谱残差。
谱残差的定义:首先,从投资组合理论中引入一些概念。假设r是一个均值为零、协方差为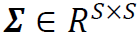 的随机向量,表示S支股票在给定的投资期限内的收益。由于Σ是对称的,存在分解
的随机向量,表示S支股票在给定的投资期限内的收益。由于Σ是对称的,存在分解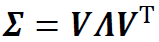 ,其中
,其中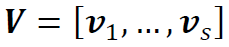 为正交矩阵,
为正交矩阵,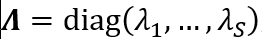 是对角线元素为特征值的对角矩阵。然后,我们可以构建一个新的随机向量
是对角线元素为特征值的对角矩阵。然后,我们可以构建一个新的随机向量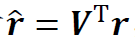 ,其坐标分量
,其坐标分量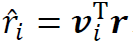 互不相关。在投资组合理论中,
互不相关。在投资组合理论中,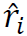 被称为主要投资组合(Partovi and Caputo 2004)。主要投资组合已被用于“风险平价”方法,以分散市场上内在风险来源的风险(Meucci 2009)。
被称为主要投资组合(Partovi and Caputo 2004)。主要投资组合已被用于“风险平价”方法,以分散市场上内在风险来源的风险(Meucci 2009)。
由于第i个主要投资组合的波动率(即标准差)为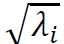 ,因此原始收益序列对具有较大特征值的主要投资组合有较大的风险敞口。例如,第一主要投资组合可以被视为与整体市场对应的因子(Meucci 2009)。因此,为了对冲共同市场因子,一个自然的想法是舍弃几个特征值最大的主要投资组合。形式上,我们对谱残差定义如下。
,因此原始收益序列对具有较大特征值的主要投资组合有较大的风险敞口。例如,第一主要投资组合可以被视为与整体市场对应的因子(Meucci 2009)。因此,为了对冲共同市场因子,一个自然的想法是舍弃几个特征值最大的主要投资组合。形式上,我们对谱残差定义如下。
定义2 设C(<S)为给定的正整数。定义谱残差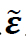 为通过将原始收益向量r投影到特征值最小的S-C个主要投资组合所成的空间上而得到的向量。
为通过将原始收益向量r投影到特征值最小的S-C个主要投资组合所成的空间上而得到的向量。
在实践中,我们计算谱残差的经验版本如下。给定时间窗口H>1,定义窗口信号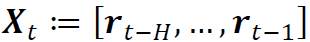 ,并用
,并用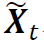 表示由
表示由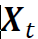 减去行向量的经验均值后得到的矩阵。通过奇异值分解(SVD),
减去行向量的经验均值后得到的矩阵。通过奇异值分解(SVD),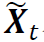 可以分解为
可以分解为
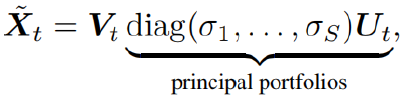
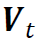 是一个S×S维的正交矩阵,
是一个S×S维的正交矩阵,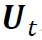 是一个S×H维的矩阵,其行向量为相互正交的单位向量,
是一个S×H维的矩阵,其行向量为相互正交的单位向量,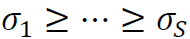 为奇异值。注意到,
为奇异值。注意到,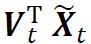 为主要投资组合的已实现收益,那么,计算s(t-H≤s≤t-1)时刻的经验谱残差的计算公式为
为主要投资组合的已实现收益,那么,计算s(t-H≤s≤t-1)时刻的经验谱残差的计算公式为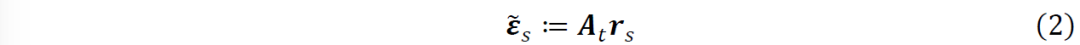
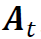 为投影矩阵,其定义为
为投影矩阵,其定义为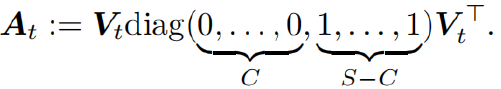
与因子模型的关系 尽管我们通过PCA定义了谱残差,但它们也与生成模型(1)相关,从而传递了原始意义上“残差因子”的信息。
金融文献指出,仅依赖于式(1)中残差因子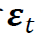 的交易策略可以对整体市场的结构变化保持稳健性(Blitz, Huij, and Martens 2011; Blitz et al. 2013)。虽然线性因子模型(1)中的参数估计通常基于因子分析(FA)方法(Bartholomew, Knott, and Moustaki 2011),但谱残差
的交易策略可以对整体市场的结构变化保持稳健性(Blitz, Huij, and Martens 2011; Blitz et al. 2013)。虽然线性因子模型(1)中的参数估计通常基于因子分析(FA)方法(Bartholomew, Knott, and Moustaki 2011),但谱残差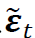 与从FA中得到的残差因子并不完全相同。尽管如此,我们可以证明以下结果,即在合适的条件下,谱残差能够对冲共同市场因子。
与从FA中得到的残差因子并不完全相同。尽管如此,我们可以证明以下结果,即在合适的条件下,谱残差能够对冲共同市场因子。
命题1 设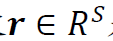 是由线性模型
是由线性模型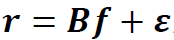 生成的随机向量,其中B为S×C维矩阵,
生成的随机向量,其中B为S×C维矩阵,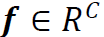 ,
,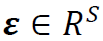 为零均值随机向量。假定以下条件成立:
为零均值随机向量。假定以下条件成立:
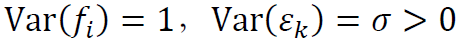
f和ε的坐标分量互不相关,即对任意的
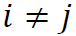 和
和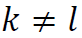 ,成立
,成立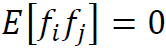 ,
,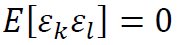 ,
,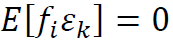 。
。
那么,我们有
(i). 式(2)中定义的谱残差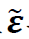 与共同因子f不相关。
与共同因子f不相关。
(ii). 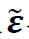 的协方差矩阵为
的协方差矩阵为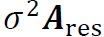 ,在适当的假设下可以近似为对角矩阵,这意味着谱残差
,在适当的假设下可以近似为对角矩阵,这意味着谱残差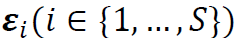 的坐标变量几乎是不相关的。
的坐标变量几乎是不相关的。
在上述命题中,第一个命题(i)表明,谱残差可以在不知道确切的残差因子的情况下消除共同因子。后一个命题(ii)证明了预测的协方差矩阵可以近似为对角矩阵,这将在下一小节中使用。为完整起见,我们在附录B中提供了证明。此外,ε是各向同性的假设可以在以下意义上得到放宽。如果我们假设残差因子ε是几乎各向同性的,且共同因子Bf比ε具有更大的波动贡献,那么可以证明在谱残差中使用的线性变换接近于消除市场因子的投影矩阵。由于形式上的表述有些复杂,我们在附录B中给出了详细证明。
此外,谱残差的计算速度明显快于基于FA的方法,这是因为FA通常需要反复执行SVD来解决非凸优化问题,而谱残差只需要一次。第4.2节给出了运行时间的实验比较。
我们的下一个目标是根据提取的信息构建投资组合。为此,我们在这里介绍一种预测谱残差未来分布的方法,并解释如何将分布特征转化为可执行的投资组合。
分布预测 给定已实现残差因子序列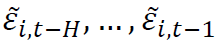 ,考虑预测未来观测值
,考虑预测未来观测值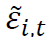 的分布问题。我们的方法是使用一个学习条件分布
的分布问题。我们的方法是使用一个学习条件分布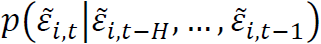 的预测器。由于我们的最终目标是构建投资组合,因此我们只使用预测的均值和协方差,而不需要条件分布的完整信息。尽管如此,拟合正态分布等对称模型可能会有问题,因为众所周知,收益率的分布往往是偏斜的(Cont 2000; Lin and Liu 2018)。为了避免这一点,我们利用分位数回归(Koenker 2005)这一现成的非参数方法来估计条件分位数。直观地说,如果我们获得了目标变量的足够多的分位数,我们就可以重建该变量的任何分布性质。我们训练一个预测多个条件分位数的函数ψ,并将其输出转换为条件均值和方差的估计量。整个过程是可微的,因此我们可以将其纳入现代深度学习框架。
的预测器。由于我们的最终目标是构建投资组合,因此我们只使用预测的均值和协方差,而不需要条件分布的完整信息。尽管如此,拟合正态分布等对称模型可能会有问题,因为众所周知,收益率的分布往往是偏斜的(Cont 2000; Lin and Liu 2018)。为了避免这一点,我们利用分位数回归(Koenker 2005)这一现成的非参数方法来估计条件分位数。直观地说,如果我们获得了目标变量的足够多的分位数,我们就可以重建该变量的任何分布性质。我们训练一个预测多个条件分位数的函数ψ,并将其输出转换为条件均值和方差的估计量。整个过程是可微的,因此我们可以将其纳入现代深度学习框架。
下面我们将详细介绍上述步骤。首先,我们概述一下分位数回归的目标。设Y是一个标量随机变量,X是另外的随机变量。对于α∈(0,1),给定X=x,Y的条件α分位数被定义为
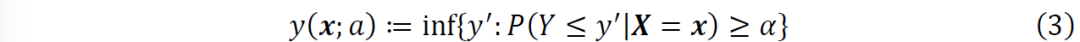
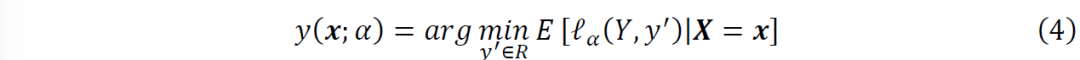
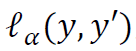 为弹球损失函数,定义为
为弹球损失函数,定义为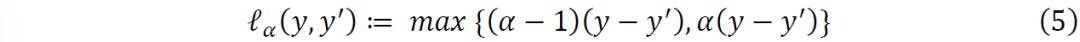
对于当前情况,目标变量是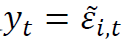 ,解释变量是
,解释变量是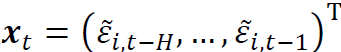 。我们希望构造一个函数
。我们希望构造一个函数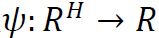 来估计
来估计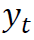 的条件
的条件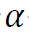 分位数。为此,分位数回归试图解决以下最小化问题
分位数。为此,分位数回归试图解决以下最小化问题
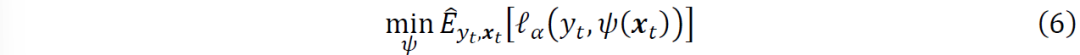
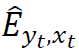 为在整个时间范围内关于
为在整个时间范围内关于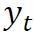 和
和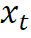 的经验期望。我们应该注意到Biau和Patra(2011)的研究中也考虑了分位数回归预测时间序列条件分位数的类似应用。
的经验期望。我们应该注意到Biau和Patra(2011)的研究中也考虑了分位数回归预测时间序列条件分位数的类似应用。接下来,设Q>0为给定整数,并设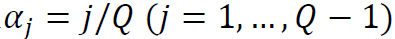 为等距分位数网格。我们考虑通过函数
为等距分位数网格。我们考虑通过函数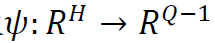 同时估计α分位数的问题,为此,定义损失函数为
同时估计α分位数的问题,为此,定义损失函数为
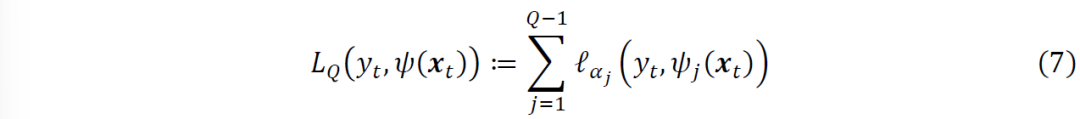
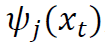 是
是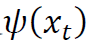 的第j个坐标分量。
的第j个坐标分量。一旦我们得到估计的Q-1个分位数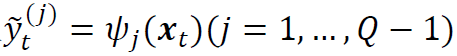 ,我们就可以估计目标变量
,我们就可以估计目标变量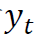 的未来均值为
的未来均值为
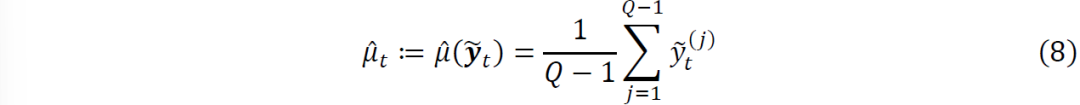
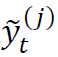 的样本方差来估计未来的方差
的样本方差来估计未来的方差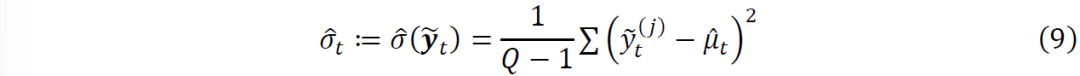
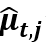 和谱残差
和谱残差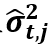 的预测值,第j个资产的权重为
的预测值,第j个资产的权重为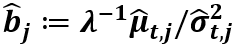 。
。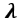 。详见附录A.1。
。详见附录A.1。对于分位数预测模型ψ,我们引入了两种神经网络模型架构,它们都考虑了金融学中研究的尺度不变性。
波动率不变性 首先,我们考虑金融时间序列振幅的不变性。众所周知,金融时间序列数据表现出一种称为波动聚集的特性(Mandelbrot 1997)。粗略地说,波动聚类效应描述了这样一种现象:金融时间序列的大幅波动往往伴随着下一时段的大幅波动,而小幅波动往往伴随着下一时段的小幅波动。因此,如果我们可以将某一信号看作金融时间序列,那么通过正标量乘法得到的信号可以被视为金融时间序列的另一种可信实现。
为了将这种振幅不变性纳入模型架构中,我们利用了正齐次函数类。这里,称函数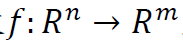 是正齐次的,若
是正齐次的,若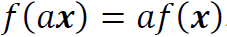 对任何
对任何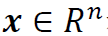 和
和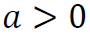 成立。例如,我们可以发现,任何线性函数和任何没有偏置项的ReLU神经网络都是正齐次的。更一般地,我们可以对正齐次函数类进行如下建模。设
成立。例如,我们可以发现,任何线性函数和任何没有偏置项的ReLU神经网络都是正齐次的。更一般地,我们可以对正齐次函数类进行如下建模。设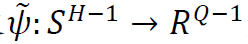 是定义在H-1维球体上的任意
是定义在H-1维球体上的任意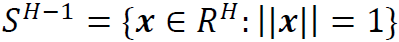 。然后,我们得到正齐次函数
。然后,我们得到正齐次函数
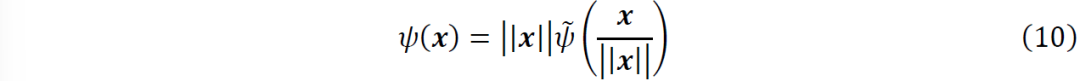
因此,我们可以将球面上的任何函数类转换为振幅不变预测模型。
时间尺度不变性 其次,我们考虑时间尺度的不变性。有一个众所周知的假设,即股票价格的时间序列具有分形结构(Peters 1994)。分形结构是指序列的自相似性。也就是说,如果我们在几个不同的采样率中观察序列,我们就不能从下采样序列的形状中推断出潜在的采样率。分形结构已在多个实际市场中观察到(Cao, Cao, and Xu 2013; Mensi et al. 2018; Lee et al. 2018)。有关这一特性的进一步讨论,请参见附录A.2中的注释1。
为了利用分形结构的优势,我们提出了一种新颖的网络结构,我们称为分形网络。其主要思想是,我们通过对具有不同采样率的多个子序列应用一个共同操作来有效地利用自相似性。通过这种方法,我们预计可以提高采样效率,并减少需要训练的参数数量。
在此,我们将简要介绍所提架构,同时将在附录A.2中给出更详细的解释。我们的模型由两部分组成:(a)重采样机制;(b)两个神经网络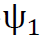 和
和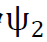 。我们模型的输入输出关系描述如下。首先,给定单个股票收益序列x,重采样机制Resample(x, τ)会生成一个序列,该序列与尺度参数0<τ≤1指定的采样率相对应。我们对L个不同的参数
。我们模型的输入输出关系描述如下。首先,给定单个股票收益序列x,重采样机制Resample(x, τ)会生成一个序列,该序列与尺度参数0<τ≤1指定的采样率相对应。我们对L个不同的参数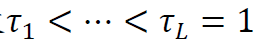 ,生成L个序列。接着,我们应用一个由神经网络建模的普通非线性变换
,生成L个序列。接着,我们应用一个由神经网络建模的普通非线性变换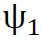 。最后,通过提取这些序列的经验平均值,我们汇总了不同采样率的信息,并应用另一个网络
。最后,通过提取这些序列的经验平均值,我们汇总了不同采样率的信息,并应用另一个网络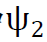 。总之,整个过程可以用以下方程来表示
。总之,整个过程可以用以下方程来表示
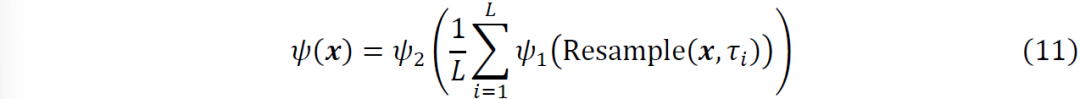
04
我们使用开盘价的原因如下。首先,开盘时段的交易量大于收盘时段的交易量(Amihud and Mendelson 1987),这意味着用开盘价交易实际上比用收盘价交易更容易。此外,金融机构不能在收盘期间大量交易股票,因为这会被视为一种非法行为,即所谓的“尾盘冲击”。
共同实验设置 我们采用延迟参数d=1(即延迟一天)来更新投资组合。我们将回溯窗口大小设为H=256,即所有预测模型都可以使用之前256个交易日的历史股票价格。有关实验中使用的其他参数参见附录C.3。
评估指标 我们列出了在整个实验中使用的评估指标。
累积财富(CW)是交易策略产生的总回报: 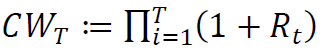
年化收益率(AR)是投资期限为一年所获的收益率,定义为 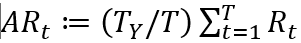 ,其中T_Y是一年中的平均持有期数
,其中T_Y是一年中的平均持有期数年化波动率(AVOL)的定义为 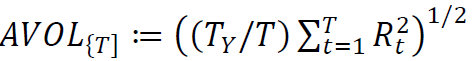
年化夏普比率(ASR)是风险调整后的年化收益率(Sharpe 1994),定义为 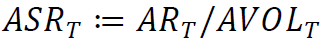
如第3.1节所述,谱残差可用于对冲市场因子的风险敞口。为了验证这一点,我们比较了基于以下因子的交易策略表现:(i) 原始收益;(ii) 因子分析(FA)提取的残差因子;(iii) 谱残差。
对于FA,我们采用最大似然法(Bartholomew, Knott, and Moustaki 2011)拟合K=30的因子模型(1),并提取残差因子作为剩余部分。关于谱残差,我们通过从原始收益中减去C=30个主成分来得到残差序列。我们将这两种方法应用于长度为H=256的窗口数据。
为了不影响训练算法的选择,我们使用了一种简单的反转策略。确切地说,对于原始收益序列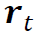 ,我们使用的是一种确定性策略,将前一个观测值
,我们使用的是一种确定性策略,将前一个观测值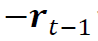 的相反数归一化为零投资组合(精确公式见附录C.2)。我们用类似方法定义了残差序列的反转策略。
的相反数归一化为零投资组合(精确公式见附录C.2)。我们用类似方法定义了残差序列的反转策略。
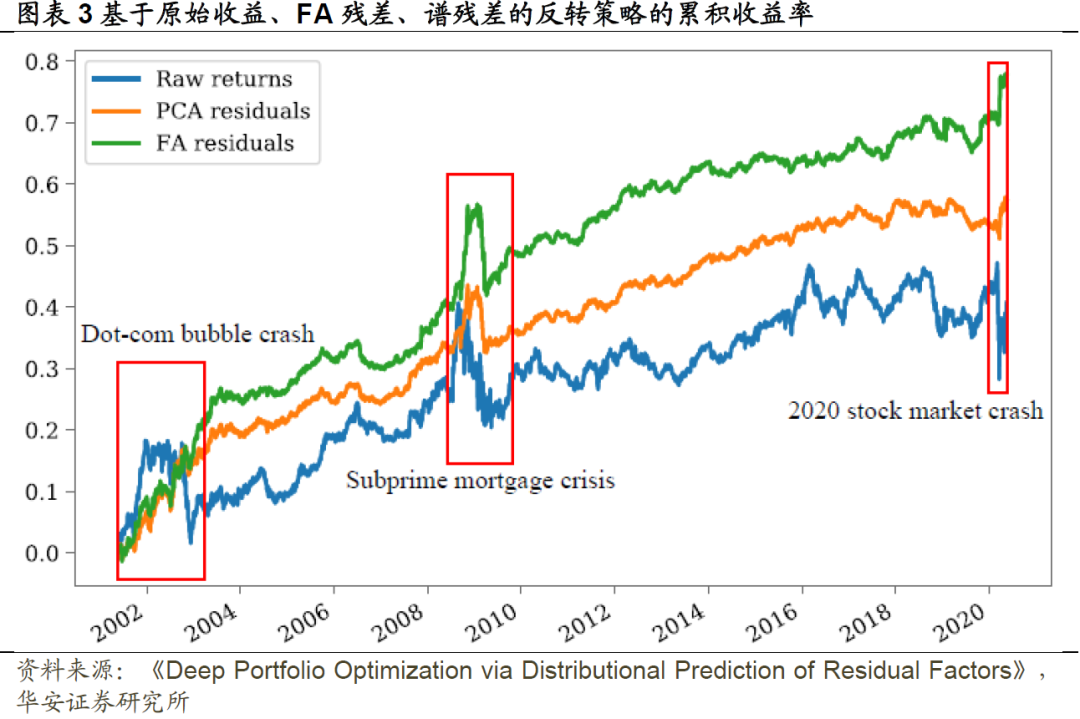
图表3展示了在日本市场数据上执行反转策略的累计收益率。我们看到,基于原始收益的反转策略受到几次重大金融危机的严重影响,包括2000年代初的互联网泡沫破裂、2008年的次贷危机和2020年的股市崩盘。另一方面,两种基于残差的策略似乎对这些金融危机更为稳健。在累计收益方面,谱残差与FA残差表现相似。此外,就夏普比率而言,谱残差(2.86)的表现优于FA残差(2.64)。
值得注意的是,谱残差的计算速度比FA残差快得多。特别是,我们使用包含5000天内所有股票价格记录的整个数据集计算了这两个残差。对于PCA和FA,我们使用了scikit-learn软件包(Pedregosa et al. 2011)中的实现方法,所有计算均在Intel Xeon Gold 6254处理器(3.1GHz)的18个CPU内核上运行。然后,提取谱残差耗时约10分钟,而FA耗时约13小时。
我们在美国市场数据上评估了第3节所述的系统性能。日本市场数据的相应结果见附录E。
基线方法 我们将所提出的系统与以下基线进行比较:(i) Market代表统一的买入并持有策略。(ii) AR(1)代表所有系数均为-1的AR(1)模型,这可视为简单的反转策略。(iii) Linear代表基于以往H个原始收益率的普通线性回归收益预测模型。(iv) MLP代表基于带批量归一化和dropout的多层感知器收益预测模型(Pal and Mitra 1992; Ioffe and Szegedy 2015; Srivastava et al. 2014)。(v) SFM是基于状态频率记忆RNN的最先进股价预测算法之一(Zhang, Aggarwal, and Qi 2017)。
此外,我们还将我们提出的系统(DPO)与一些消融模型进行了比较,这些模型与DPO相似,除了以下几点:
无分位数预测DPO(DPO-NQ)不使用分布预测的信息,而是输出经L_2损失训练的条件均值
无分形网络 DPO(DPO-NF)使用简单的多层感知器代替分形网络
无波动归一化DPO(DPO-NV)不使用分形网络中的归一化(见式(10))
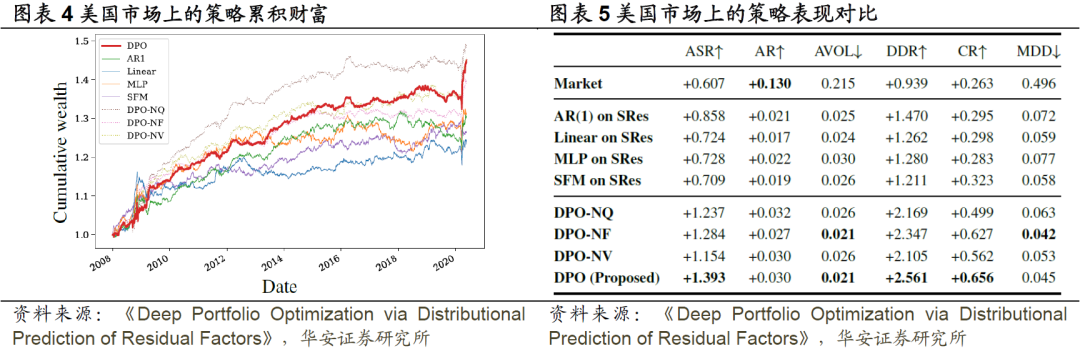
真实市场数据的表现 图表4展示了在美国市场取得的累计财富(CW)。图表5展示了第4.1节中的其他评估指标的结果。对于谱残差的参数C,我们使用了C=10,这是我们根据训练数据确定的(详见附录D.2)。总体而言,我们提出的DPO方法在多个评估指标上都优于基线方法。关于与三种消融模型的比较,我们有以下结论:
1. 分布预测的影响。我们发现,引入分布预测能明显改善ASR。虽然DPO-NQ 取得了最佳的CW,但DPO在ASR上的表现更好。这表明,在没有方差预测的情况下,DPO-NQ倾向于追求收益,而不考虑承担风险。总体而言,我们观察到DPO 在降低AVOL的同时未损失AR。
2. 分形网络的影响。分形网络结构的引入也提高了多个评估指标的性能。在这两个市场中,我们观察到分形网络在保持AVOL的同时有助于提高AR,这表明利用收益序列的金融归纳偏差是有效的。
3. 波动归一化的影响。我们还观察了归一化(10)的影响,对比DPO和DPO-NV,归一化对AR和AVOL都有影响,并改善了ASR。这可能是因为归一化通过降低模型的自由度来提高样本效率。
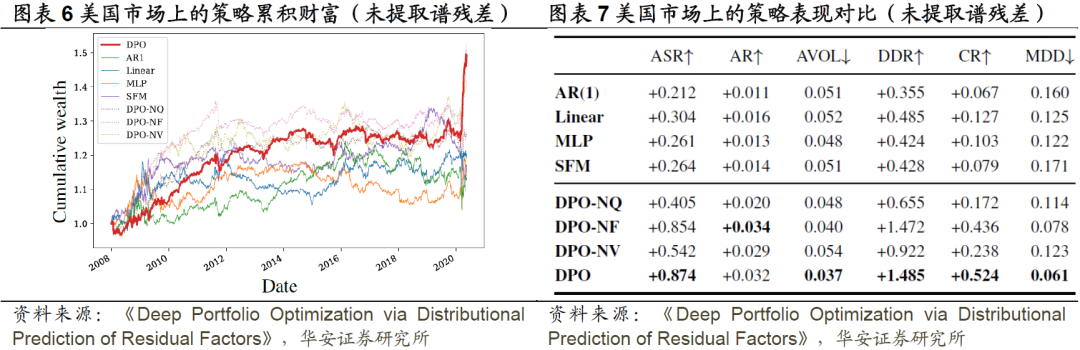
为了了解谱残差的影响,我们还对我们提出的方法和基于原始股票收益率的基线方法进行了评估,结果如图表6和图表7所示。与使用谱残差的结果相比,我们发现谱残差一致地改善了每种方法的性能。下面总结了一些更有趣的观察结果。
1. 利用谱残差,AR(1)在基线方法中取得了最好的ASR(图表5),而在原始收益序列(图表7)中却没有观察到这一点。这表明,谱残差通过抑制共同市场因子,促进了反转现象(Poterba and Summers 1988)。有趣的是,在不提取谱残差的情况下,CW在测试期间出现交叉,没有一种基线方法能始终优于其他方法(图表6)。一个可能的原因是原始股票收益之间的强相关性增加了共同市场风险的敞口。
2. 我们发现,我们的网络架构对原始序列仍然有效。特别地,DPO在多个评估指标上的表现优于所有其他方法。
05
基于因子模型的交易是量化投资组合管理的流行策略之一(e.g., Nakagawa, Uchida, and Aoshima 2018)。最著名的因子模型之一是 Fama和French所提出的三因子模型(Fama and French 1992, 1993),他们用市场回报因子、规模(市值)因子和价值(账面市值)因子来解释美国股票市场回报。
历史上,残差因子被视为因子模型中的误差(Sharpe 1964)。然而,部分研究者(Blitz, Huij, and Martens 2011; Blitz et al. 2013)认为残差因子存在可预测性。在现代投资组合理论中,投资收益的相关性越低,风险调整后的收益就越大(Markowitz 1952)。从本质上讲,残差因子的相关性比原始股票收益的相关性更小。因此,有研究证明,残差因子能够获得更大的风险调整收益(Blitz, Huij, and Martens 2011; Blitz et al. 2013)。
随着近年来深度学习的发展,各种深度神经网络被应用于股价预测(Chen et al. 2019)。一些用于时间序列的深度神经网络也被应用于股价预测(Fischer and Krauss 2018)。与其他经典机器学习方法相比,如果有足够的数据量和计算资源,深度学习可以在较少先验表征假设的情况下进行学习。即使数据不足,在网络架构中引入归纳偏差仍能促进深度学习(Battaglia et al. 2018)。技术指标经常被用于股票预测(e.g., (Metghalchi, Marcucci, and Chang 2012; Neely et al. 2014)),以及将技术指标作为神经网络的归纳偏置(e.g., Li et al. 2019)。Zhang等人(2017)使用了一种可以分析频域的循环模型,以区分不同频率的交易模式。
06
我们提出了一种构建投资组合的系统。其关键技术要素包括:(i) 基于谱分解的对冲共同市场因子的方法;(ii) 基于一种能够反映金融归纳偏差的新颖的神经网络架构的分布预测方法。通过对真实市场数据的实证评估,我们证明了所提出的方法显著提高投资组合在多个评价指标上的性能。此外,我们还验证了我们提出的每种技术本身都是有效的,我们相信我们的技术可能会在各种金融问题中得到广泛应用。
文献来源:
核心内容摘选自Imajo, K., Minami, K., Ito, K., & Nakagawa, K. 2021.5.18发布在AAAI的文章《Deep Portfolio Optimization via Distributional Prediction of Residual Factors》
风险提示
文献结论基于历史数据与海外文献进行总结;不构成任何投资建议。
50.《投资者评价基金时会考虑哪些因素?》
157.《2023年2亿规模A类户理想打新收益率3.63%》
142.《多只新股上市首日涨幅超100%,情绪维持”高温“》
138.《新股市场受资金追捧,打新收益陡升》
122.《科创板新股首日涨幅回暖,首批注册制主板新股迎来上市》
49.《多只新股破发,打新收益曲线调整》
43.《打新账户数量企稳,预计全年2亿A类收益率11.86%》


有态度的金融工程&FOF研究

本篇文章来源于微信公众号: 金工严选