引入宏观维度的改进DTW算法在择时策略中的应用——技术择时系列研究
本文基于一种相似性度量方法——改进DTW算法,引入宏观维度,应用于指数择时,构建Macro-Ita-DTW择时策略。报告的主要结论如下:
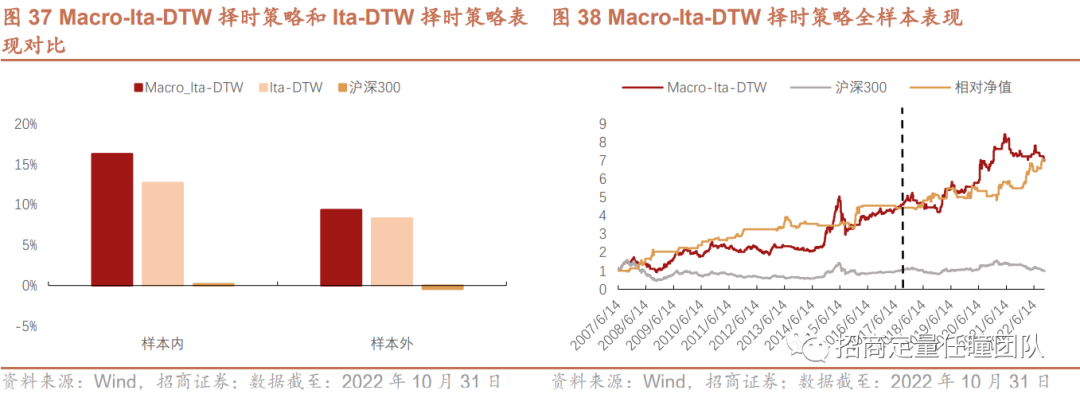
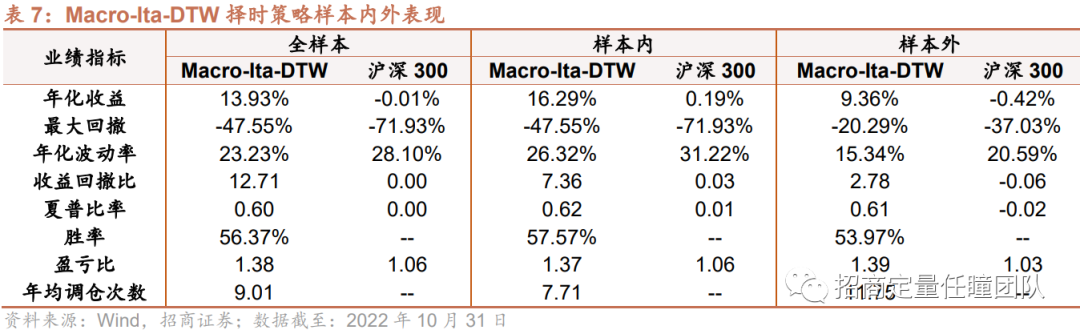
本文基于改进的DTW算法,在传统DTW算法基础上对弯曲匹配路径施加约束条件,并应用于指数择时。实证结果显示,基于Ita-DTW算法的沪深300择时策略样本内年化收益12.72%,胜率56.77%,盈亏比1.33,样本外年化收益8.33%,胜率53.57%,盈亏比1.36,且回撤显著低于标的指数,整体表现相对传统DTW择时策略有显著提升。
此外,本文引入宏观流动性指标对Ita-DTW择时策略进行优化改进。Macro-Ita-DTW择时策略样本内年化收益16.29%,胜率57.57%,盈亏比1.37,样本外年化收益9.36%,胜率53.97%,盈亏比1.39,回撤和波动水平较小,整体表现相对Ita-DTW择时策略有显著提升,且分年度表现也十分稳定。
最后,将Macro-Ita-DTW择时策略应用在其他宽基指数上,发现也能获得较好的择时效果。
*风险提示:历史数据不代表未来,模型存在失效风险。
前言
《旧唐书·魏徵传》中,唐太宗谓梁公(随身侍臣)曰:“以铜为镜,可以正衣冠;以古为镜,可以知兴替;以人为镜,可以明得失。”在金融市场中,可以回顾市场的历史表现和事件,与当下行情进行对比,从而来对未来市场趋势做出预判,即择时。择时方法有很多类型:在宏观层面,可以考察经济增速、流动性、通货膨胀、经济政策等;在中观层面,可以考察行业景气度、估值、投融资情况等;在微观层面,可以考察技术指标或市场情绪等,如价格、成交量、资金流以及衍生指标。本文旨从微观层面,基于技术(量价)指标构建择时策略。
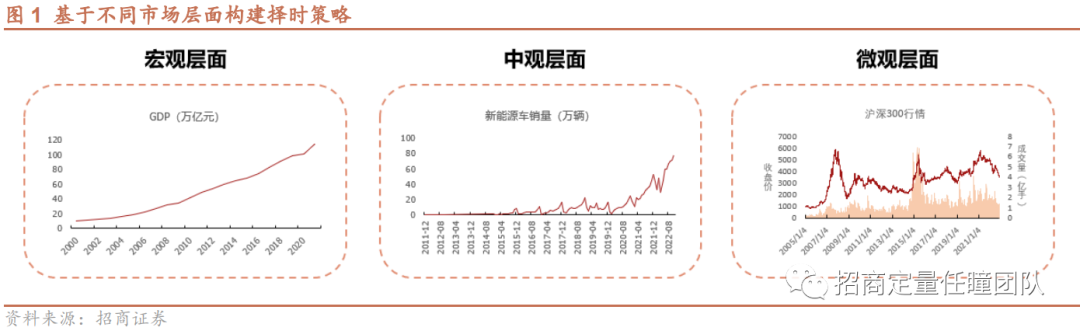
基于量价指标构建择时策略也有很多不同做法:一种是基于量价数据构造因子或择时信号,如均线择时、MACD择时、北向资金择时等;一种是基于形态/模式识别的择时策略,例如基于DTW、SVM、HMM等机器学习以及深度学习算法。本文将从形态识别的角度出发,基于动态时间弯曲(DTW)算法,构建择时策略。
本文的结构如下:第二章介绍相似性择时策略思路以及DTW算法基本原理和改进方法,第三章基于改进DTW算法在沪深300指数上进行实证分析,第四章引入宏观流动性指标对择时策略进行优化。
相似性择时及DTW算法基本原理
1.相似性择时策略思路
本文运用相似性择时策略,主要步骤如下图所示,大体思路为:考察当下指数行情与历史行情的相似度,筛选出相似度较高的若干历史行情片段作为参照,将筛选出的历史行情片段的未来涨跌幅进行平均,得到指数未来涨跌幅的预测值,最后依据该预测构建择时模型(即若预测涨跌幅>0,发出看多信号;反之发出看空信号)。
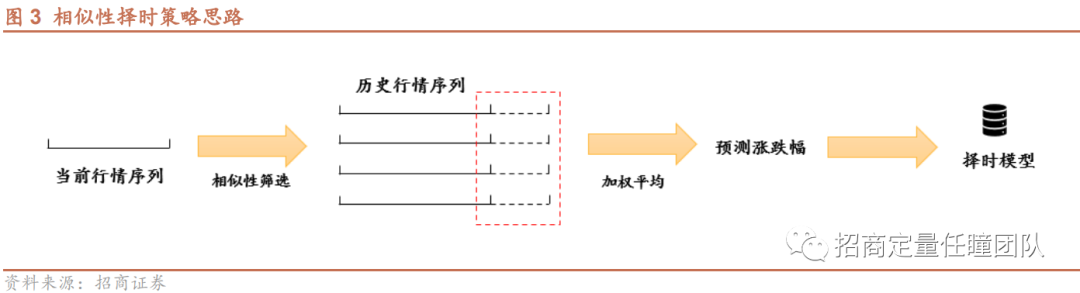
以上的策略构建思路中最关键的一步是相似性筛选,即我们用何种方法去衡量两段行情序列的相似度呢?从过往研究来看,度量时间序列相似性的方法大致分为4类:第一类为基于特征的相似性度量方法,如相关系数、互信息等;第二类为锁步(时间序列“一对一”比较)的距离度量方法,典型方法有闵可夫斯基距离(可衍生为曼哈顿距离、欧氏距离、切比雪夫距离)、Hausdorff距离、余弦相似度等;第三类为弹性(允许时间序列“一对多”比较)的距离度量方法,代表方法为动态时间弯曲距离(DTW)、编辑距离(EDR)、最长公共子序列(LCSS);第四类方法关注时间序列的变化相似性,如ARMA、HMM等。
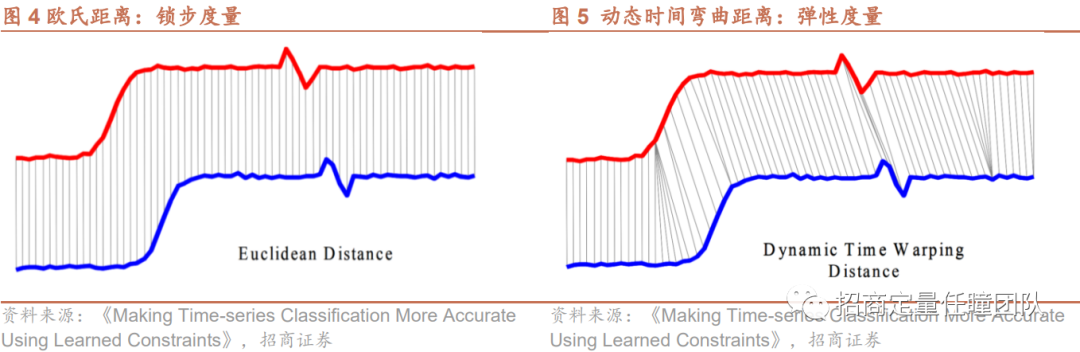
然而,基于特征的相似性度量仅提取时间序列的个别特征,忽略了部分信息,锁步度量方法(如欧氏距离)容易产生时间序列错误匹配,弹性度量能够较好地解决该问题。本文将基于一种弹性度量方法——动态时间弯曲算法来构建相似性择时策略。下面我们将回顾动态时间弯曲算法的基本原理及改进方法,2、3两节内容涉及一些理论和数学推导,读者也可选择跳过该两节的推导过程,直接进入后文策略构建内容。
2. DTW算法的基本原理
动态时间弯曲算法(Dynamic Time Warping,DTW)最早由日本学者Itakura于20世纪60年代提出,可以将两段长短不一的时间序列进行匹配,被广泛运用于语音识别领域。算法也可以很好地运用于其他领域,本节介绍DTW算法的基本原理。
对于时间序列X和Y,定义非负函数f来衡量时间序列中的点x_i和点y_j的距离:
d(i,j)=f(x_i,y_j)≥0,
除常见的欧氏距离外,距离函数f也可以选取余弦相似度、汉明距离、曼哈顿距离、切比雪夫距离等其他距离度量方法。如果时间序列是多维的,则将每个维度的距离相加即可(确保各维度量纲一致)。
定义了时间序列中点与点的距离之后,两段时间序列即可形成一个N×M的点阵,从点阵的右上角到左下角可以形成一条弯曲路径(Warping Path),如图6所示。
相较于欧氏距离等度量方法,DTW算法的优势在于能够较好地处理序列间时移或伸缩的问题,在进行距离度量时,对时间序列进行压缩、伸展或平移,是处理时间序列相似性度量问题时较为适合的经典算法。
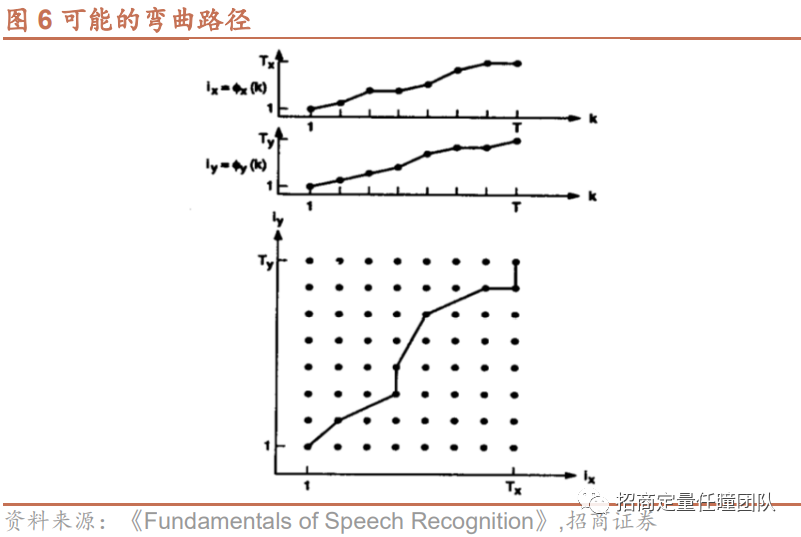
给定弯曲路径之后,便可以计算时间序列X和Y的标准化累计时间弯曲距离。另外,为了确保弯曲路径的合理性,通常需要满足3大基本条件:
· 终点条件(Endpoint Constraints):要求弯曲路径的起点和终点必须为点阵平面的对角单元;
· 连续性条件(Local Continuity Constraints):要求弯曲路径的每一步为相邻的单元(包括对角相邻单元);
· 单调性条件(Monotonicity Conditions):由于语音序列或证券交易数据等时间序列是有时序性的(时间不可倒流),所以从实际意义出发,弯曲路径在点阵图上必须是单调的。
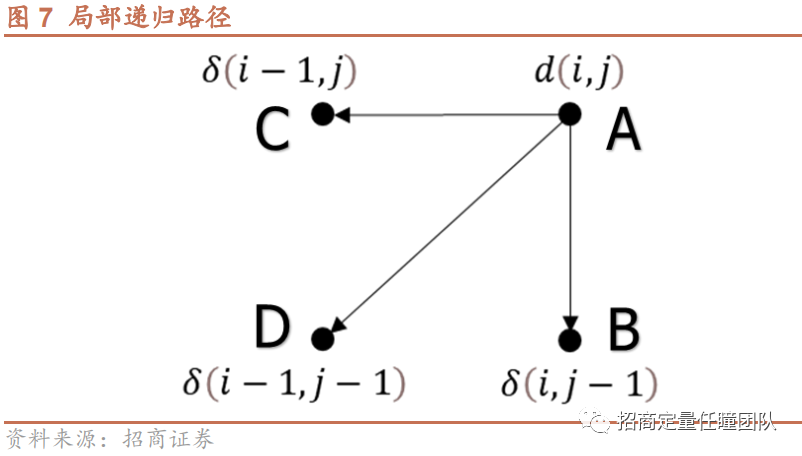
显然,满足以上3个条件的路径有很多条,选取哪条路径来计算DTW距离呢?一个很自然的想法是选取使得DTW距离最小的路径,具体推导过程需要利用动态规划算法(Dynamic Programming),这里不展开说明。最后,使得DTW距离最小化的最佳匹配路径需满足如下递归条件:
δ(i,j)=d(i,j)+min[δ(i-1,j),δ(i-1,j-1),δ(i,j-1)].
3. DTW算法的改进方法
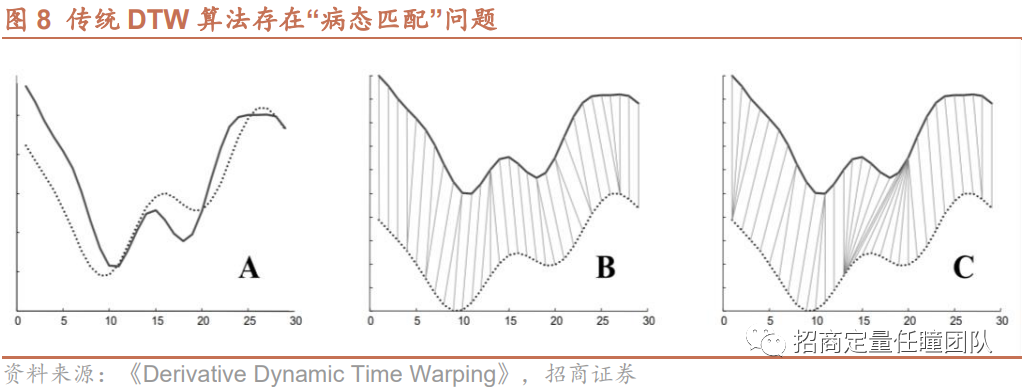
传统的DTW算法存在两点缺陷:1)算法对时间序列进行伸缩和平移时,可能存在过度伸缩或平移,产生时间序列点之间的“病态匹配”,如图8所示,B为两段时间序列的真实匹配情况,C为DTW算法下的匹配结果,显然较不合理,某些地方被过度平移和伸缩了;2)传统DTW算法运算量较大,时间复杂度较高。对于择时策略本身而言,显然第一个问题更加重要,如果不是高频策略,则运算复杂度对策略的影响不大,我们更关注距离度量的精度和策略实际效果。本节将针对“病态匹配”的问题对DTW算法做出改进,以提升匹配精度和策略效果。
如何解决“病态匹配”问题呢?很多学者提出了不同的解决方案,如加权DTW算法(Weighted Dynamic Time Warping,WDTW)、导数DTW算法(Derivative Dynamic Time Warping,DDTW)、步模式(Step Pattern)、全局约束(Global Constraints)等,本节将介绍全局约束和局部约束两类改进方法。
(1)全局约束(Global Constraints)
传统的DTW算法允许匹配路径可以在图6中的点阵中任意生成(需满足上一节的3个基本条件),全局约束要求匹配路径只能在限定的区域内生成,常用的全局约束方法有Sakoe-Chiba Constraint和Itakura Parallelogram等。
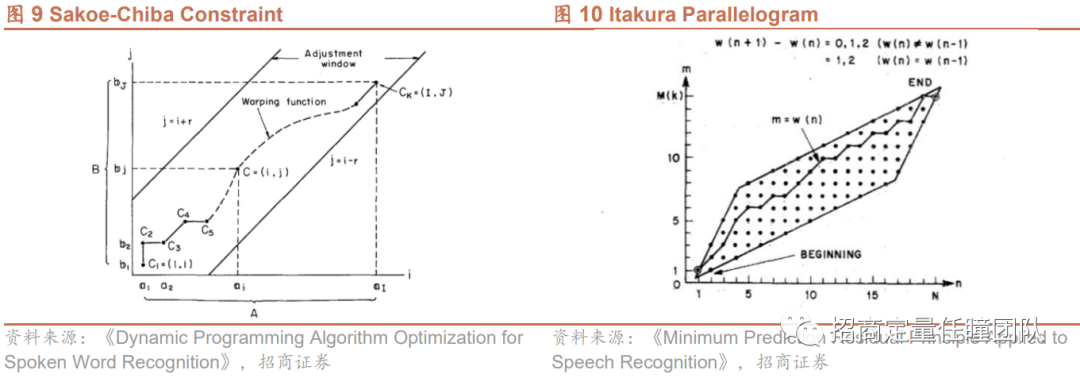
对于Sakoe-Chiba Constraint,需设定窗口限制参数r,即最佳匹配路径须在距点阵对角线距离为r的区域内;Itakura Parallelogram将匹配路径限定在一个平行四边形区域中,平行四边形的四条边的斜率分别为2和0.5。可以看出,不论是Sakoe-Chiba Constraint或Itakura Parallelogram,均要求匹配路径尽可能接近对角线,避免落在点阵的“边角区域”,即左上方区域和右下方区域,这种对匹配路径边界的限制能够尽可能避免病态匹配问题。
(2)局部约束(Local Constraints)
与全局约束是对匹配路径整体进行限制不同,局部约束是对匹配路径中每一步进行约束,两种局部约束的方法分别为步模式(Step Pattern)和加权方式(Slope Weighting)。
· 步模式
传统的DTW算法在每步进行递归时,由于单调性和连续性条件,路径只能向左方、下方或左下方的邻近点进行匹配(图7)。更一般来看,若放松连续性条件,即可以与不相邻的点匹配,便能形成新的递归方式,即步模式。常见的步模式有TypeI、TypeII、TypeIII、TypeIV、Itakura Constraint等,如下图所示。可见,不论哪种步模式,均能够较好防止路径过度弯曲,使得时间序列匹配时不会过度伸缩和平移。

· 加权方式
确定步模式之后,不同的权重参数也会对匹配路径产生影响,常见的几种加权方式如下图所示,路径上的数字即为权重。可以看出,Type(c)是非对称加权方式,其余均为对称的加权方式。

除步模式和加权方式外,还有其他改进方法,如放松终点条件(Endpoint Constraints),允许时间序列部分匹配,考虑到时间复杂度等原因,本文暂不考虑该类方法。
4.改进DTW算法在行情相似性度量上的应用
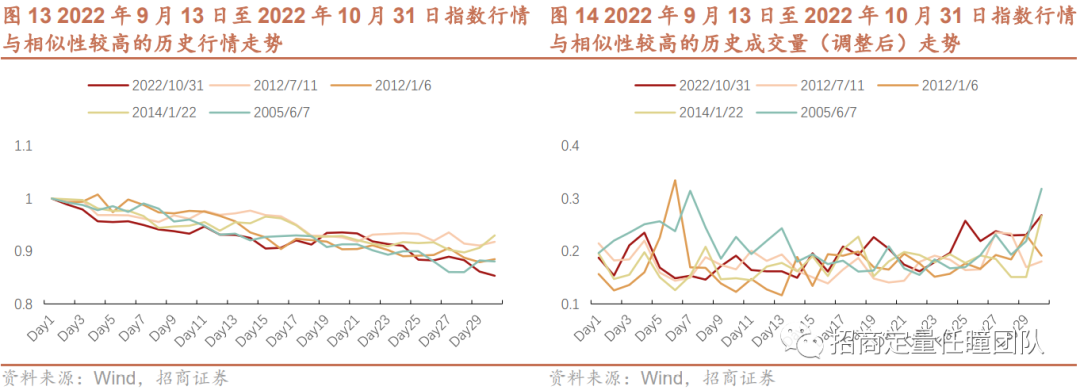
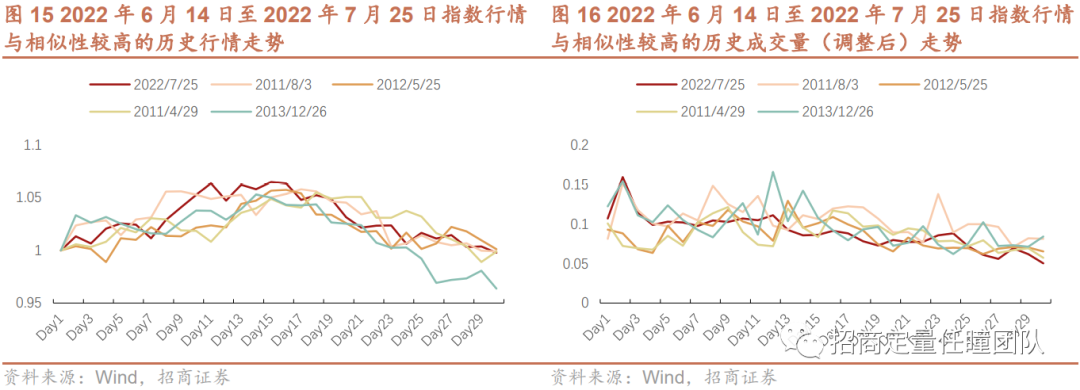
下面我们以2段历史行情为例,基于叠加Itakura Parallelogram全局约束的Ita-DTW算法对指数行情相似性进行分析测算。标的指数为沪深300,参照指标选取收盘价和成交量,序列长度为30个交易日,分别选取一段下跌行情(2022年9月13日至2022年10月31日)和一段见顶回落行情(2022年6月14日至2022年7月25日)为例进行分析。从图13-16可以看出,相似性较高的行情序列的价格走势呈现较强一致性,且成交量变化也较为一致:下跌行情的成交量经历由大变小再放大的过程,见顶回落行情的成交量在见顶之前保持相对较高水平,指数开始下跌后成交量便不断萎缩。另外,从之后5个交易日的指数表现来看,下跌行情后5个交易日的指数涨跌幅和预测涨跌幅分别为7.60%和2.22%,见顶回落行情后5个交易日的指数涨跌幅和预测涨跌幅分别为-0.57%和-0.74%,表现相对较为一致。
改进DTW算法在指数择时上的应用
上一章介绍了相似性择时的大体思路及DTW算法基本原理和几种改进方法,本章将基于传统DTW算法和改进算法在宽基指数上构建择时策略,验证改进的DTW算法在择时策略上是否有所改善和提升。
1.基于传统DTW算法的择时策略
(1)策略构建
标的指数选取沪深300,参考的技术指标选取指数收盘价和成交量,择时频率为周频。在调仓日,计算当下一段时间的技术指标序列与历史序列的DTW距离,筛选相似度较高(即DTW距离较小)的部分历史序列,根据历史序列未来一周的加权平均涨跌幅(权重=1/DTW距离)对未来一周行情做出预判,即若历史序列未来加权平均涨跌幅>0,发出看多信号,反之,发出看空信号。另外,若未筛选出相似的历史序列,则延续上一交易日的择时信号。
用来计算DTW距离进行比对的样本序列从沪深300、上证50、中证500、中证1000、上证指数等9个常见的宽基指数中选取,目的是扩充样本量,从而增强策略稳定性。数据从2005年开始,考虑到相似度比对需要用到相对较大的数据量,前500个交易日数据用来进行比对,故回测期从500个交易日后开始。另外,对参考指标进行归一化处理,以消除变量的不稳定性。
我们将回测期分为训练集(样本内)和测试集(样本外),训练集用以训练模型参数,测试集用以检验模型在样本外的泛化能力及稳定性。测试集为近5年(2017年8月22日至2022年10月31日),训练集为回测期之前的时间(2007年4月26日至2017年8月21日),可以看出,训练集和测试集均能覆盖牛市、熊市、震荡市等不同市场行情阶段。模型有2个主要参数:序列长度l和距离阈值k,其中距离阈值k设置目的是当筛选相似的历史序列时,选取距离小于k的历史序列。若k选取过小,则会遗漏相似的历史序列;若k选取过大,则实际上不相似的历史序列也会被选入。
(2)实证分析
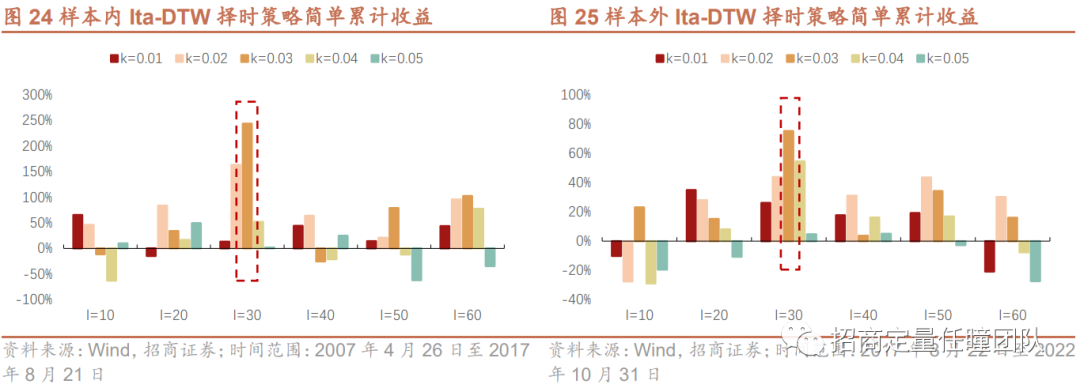
测算在训练集中,不同参数组合(l,k)下策略的收益表现,可以发现参数组合(l,k)=(30,0.02)在样本内是最优的,且该参数组合在样本外的表现也较优,说明该参数组合较为稳定,故接下来使用该参数组合进行策略构建。
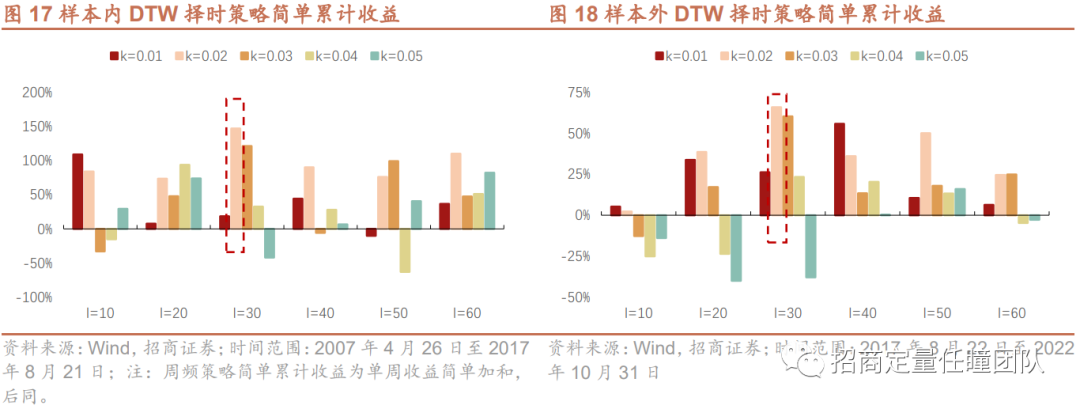
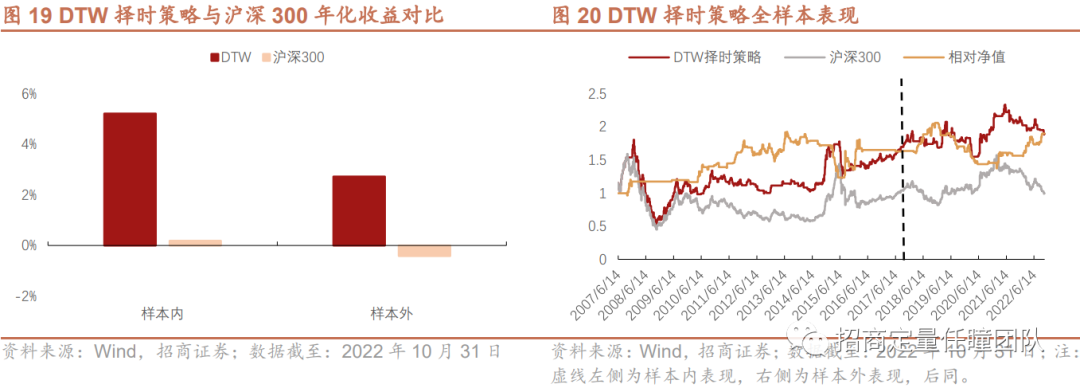
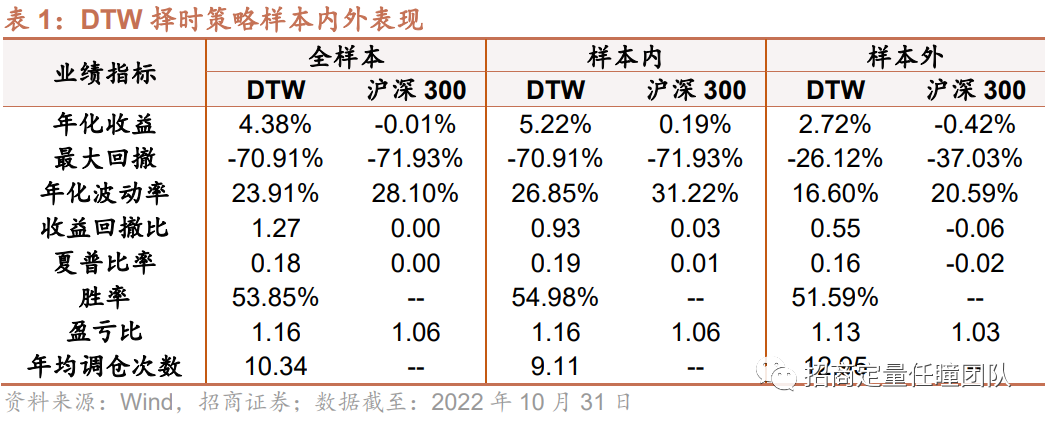
传统DTW择时策略显示出一定的效果,样本内年化收益达5.22%,超额年化达5%,样本外年化收益2.72%,超额年化超3%,另外,样本外策略的最大回撤约26.12%,显著低于沪深300同期水平(37.03%)。
2.基于改进DTW算法的择时策略
本节我们应用全局约束和局部约束对原始的DTW择时策略进行改进,验证改进的DTW择时策略的提升效果。
(1)基于全局约束的DTW择时策略
· 叠加Sakoe-Chiba Constraint窗口限制条件的SC-DTW择时策略
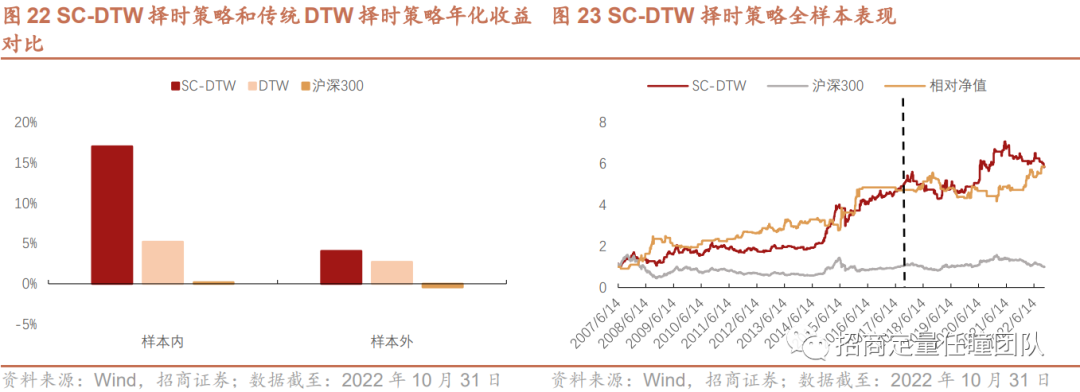
测算在训练集中,不同参数组合(l,k,r)下叠加Sakoe-Chiba Constraint约束的DTW策略(简称SC-DTW,后同)的收益表现,可以发现参数组合(l,k,r)=(30,0.03,5)在样本内是最优的。另外,值得注意的是,若r=30,则SC-DTW退化为一般的传统DTW算法。
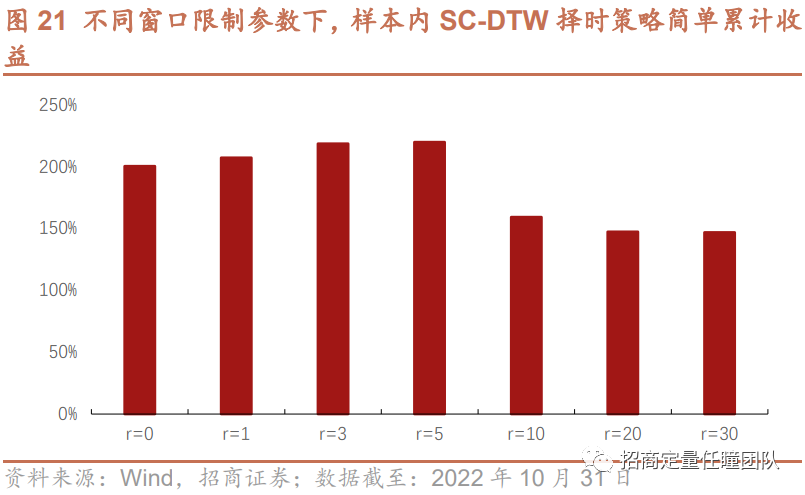
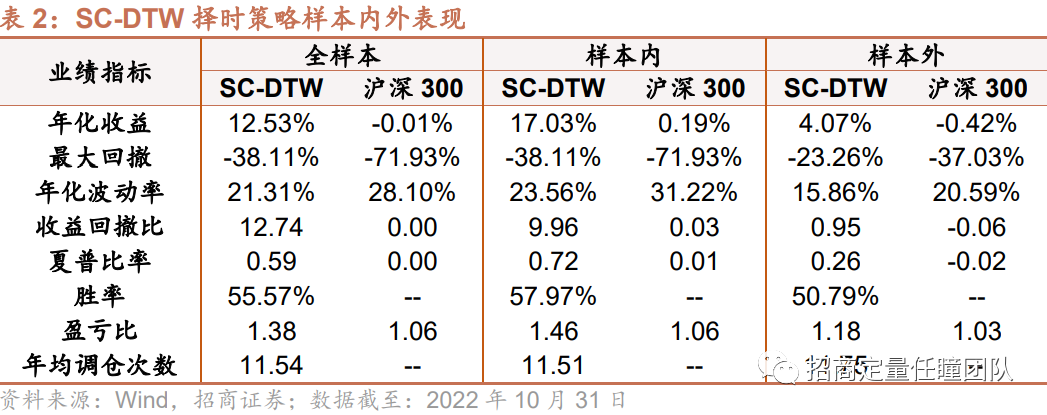
叠加Sakoe-Chiba Constraint后,DTW择时策略整体效果有所改善。样本内年化收益提升至17.03%,样本外年化收益也略有提升,约4.07%,另外,样本外策略的回撤水平和波动率也显著低于沪深300。
· 叠加Itakura Parallelogram窗口限制条件的Ita-DTW择时策略
测算在训练集中,不同参数组合(l,k)下叠加Itakura Parallelogram约束的DTW策略(简称Ita-DTW,后同)的收益表现,发现参数组合(l,k)=(30,0.03)在样本内最优,且该参数组合在样本外的表现依旧稳健,故接下来使用该参数组合进行策略构建。
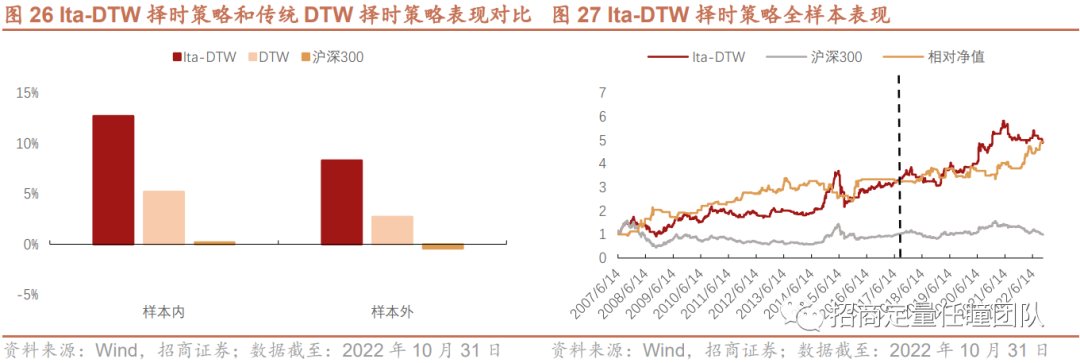
叠加Itakura Parallelogram后,DTW择时策略效果有显著改善。Ita-DTW择时策略样本内年化收益提升至12.72%,最大回撤下降到47.55%;从样本外表现来看,年化收益提升至8.33%,最大回撤下降至20.29%,收益回撤比和夏普比率也有显著改善。另外,相对于SC-DTW(需设置窗口限制参数r),Ita-DTW不需设置额外参数,故下面我们应用Itakura Parallelogram作为全局约束方法。
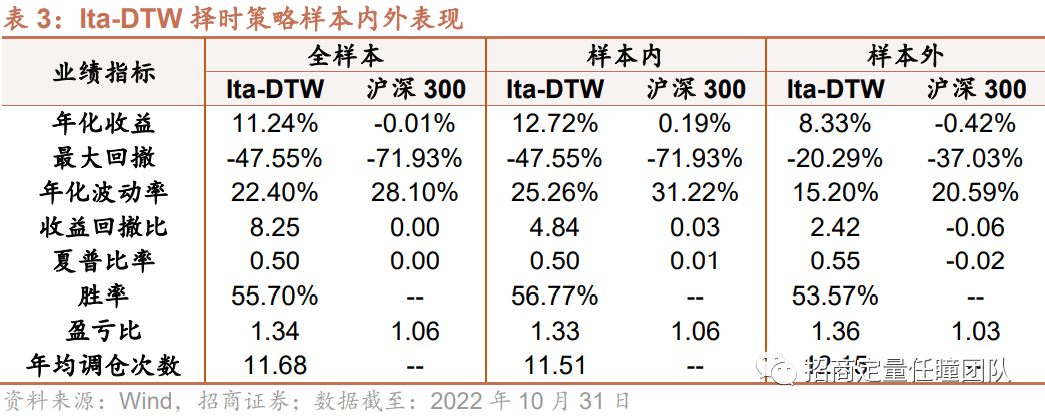
(2)基于局部约束的DTW择时策略
测算在训练集中,不同局部约束方法下DTW策略的收益表现,可以发现叠加TypeId局部约束的DTW择时策略样本内收益较高,故选取TypeId作为局部约束的方法。
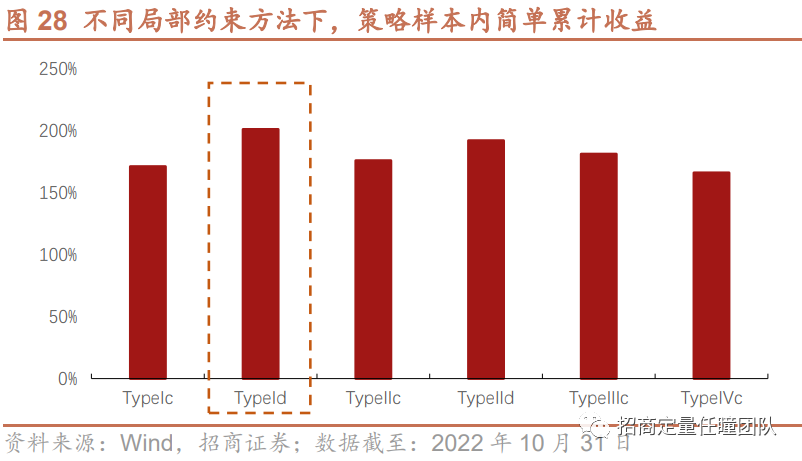
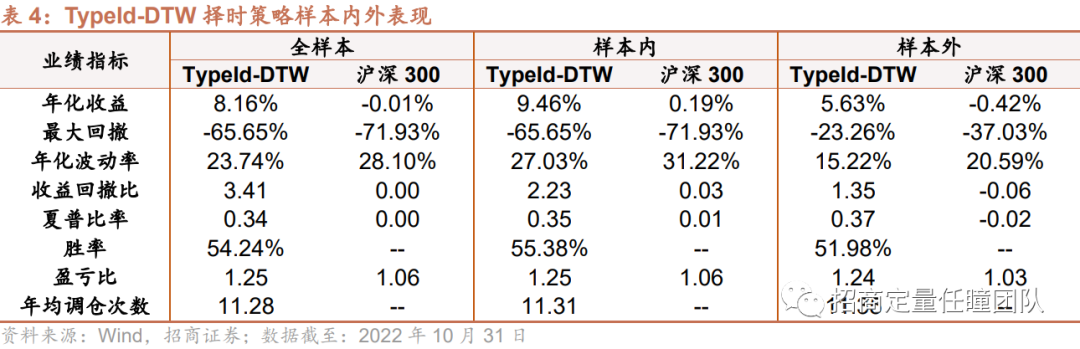
叠加TypeId局部约束后,DTW择时策略效果有所提升。样本内年化收益提升至9.46%,胜率有所提高;从样本外表现来看,年化收益提升至5.63%,最大回撤下降至23.26%,收益回撤比和夏普比率也有显著改善。
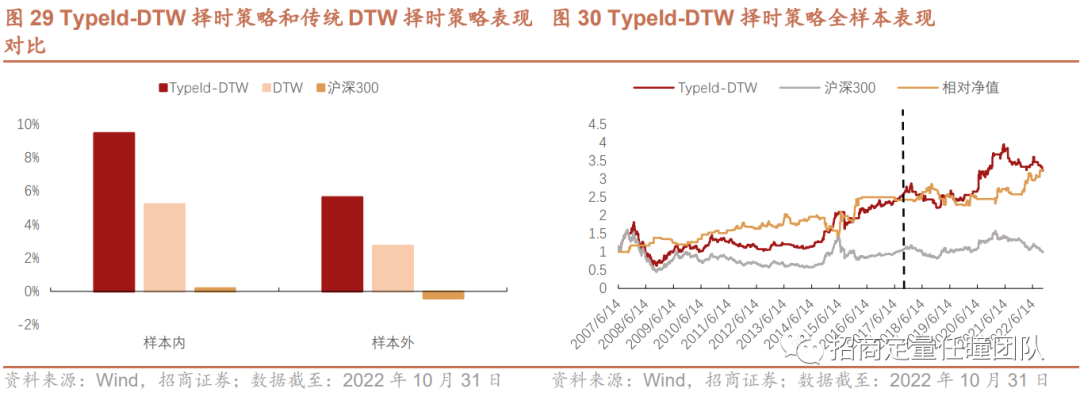
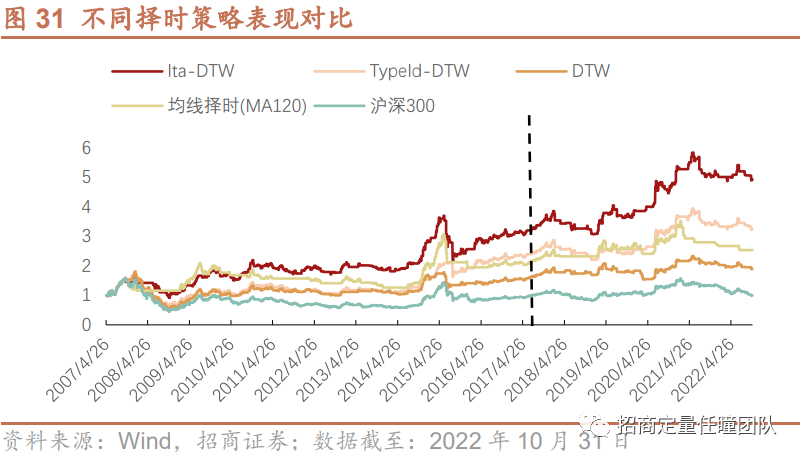
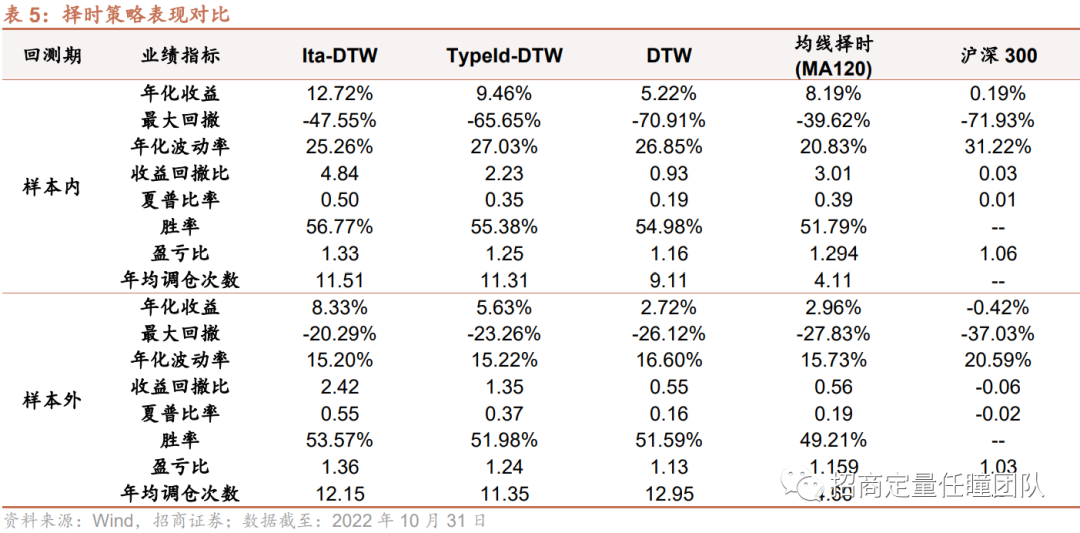
(3)不同择时策略表现对比
最后,我们对比了几种改进算法的表现,可以发现:整体来看,Ita-DTW择时策略的收益表现和风险控制能力较优,不论在样本内还是样本外,相对TypeId-DTW、传统DTW算法以及普通均线择时策略均更为优异。另外,Ita-DTW择时策略稳定性较强,样本外超额年化收益超8%,回撤显著降低,收益回撤比和夏普比率较高,策略在样本外仍能发挥出较好的择时效果。
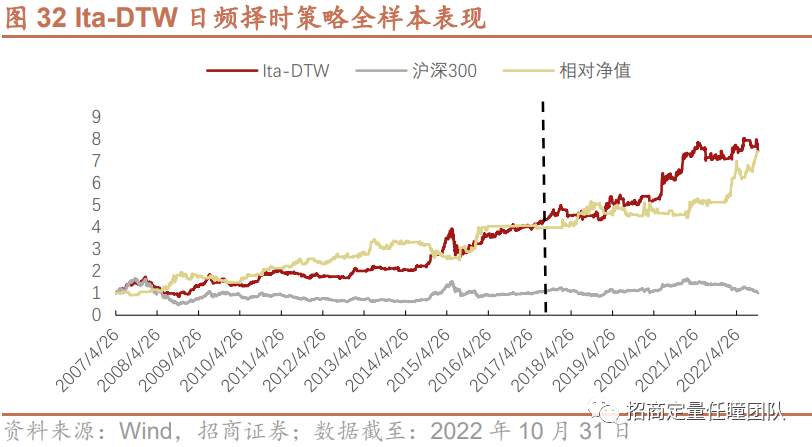
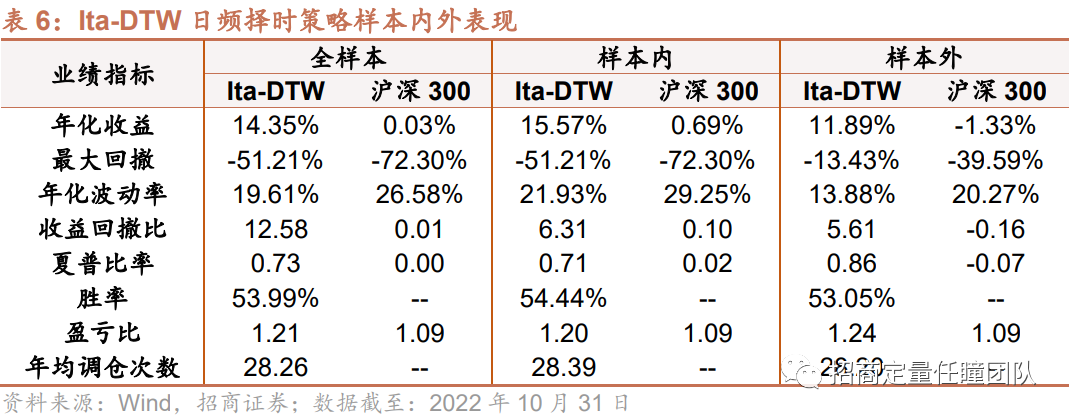
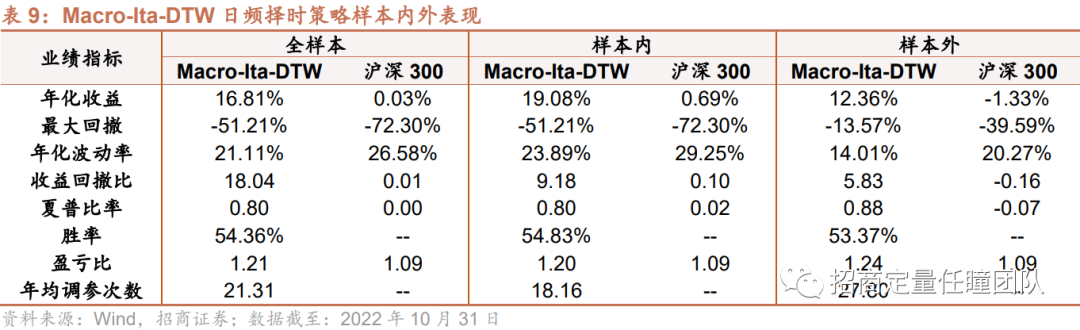
另外,我们也测试了Ita-DTW算法在日频择时上的效果,可以发现Ita-DTW在日度择时上表现也较为出色,样本内年化收益15.57%,胜率54.44%,盈亏比1.20,样本外年化收益11.89%,胜率53.05%,盈亏比1.24,且全样本最大回撤、夏普比率等均显著优于指数。
引入宏观流动性指标的Macro-Ita-DTW择时策略
基于技术指标构建的择时策略可以较好地对市场短期行情进行预判,但是纯量价分析往往忽视了市场所处的宏观环境和长期基本面趋势,难免会犯“刻舟求剑”的错误。因此,我们考虑尝试引入一个宏观维度来对模型进行优化和改进。由于中国市场的特殊性,相对于企业盈利,A股市场对流动性更为敏感,故本章将在Ita-DTW择时策略基础上,引入宏观流动性指标M1和M2剪刀差,以期提升策略效果。
1.宏观流动性指标
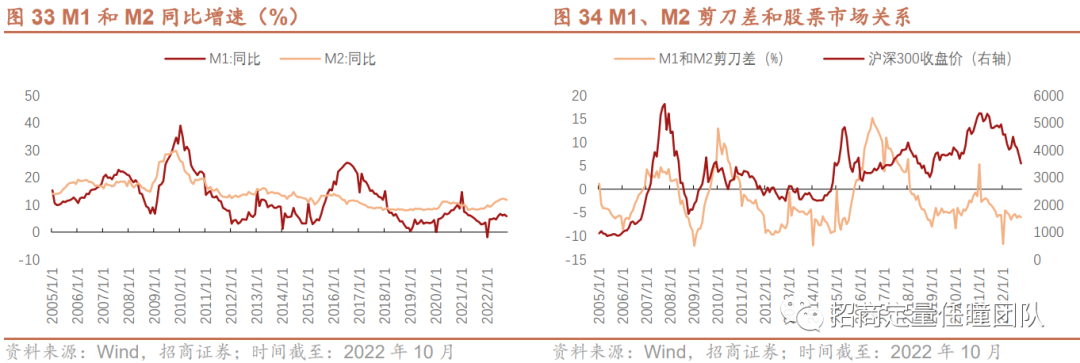
M1和M2(同比增速)的剪刀差反映货币供应量结构的变化,是能够把握市场拐点的一个宏观流动性指标。M0、M1、M2等均是反映宏观流动性的指标,M0最为活跃,与消费变动直接相关,M1反映现实购买力,是经济周期波动的先行指标,流动性次于M0,M2代表现实购买力和潜在购买力,反映社会总需求变化和通胀压力情况。从图33可以看出,M1相较M2变动更大,说明M1活跃度更高。
M1和M2剪刀差呈现较强的周期性,与市场指数相关性较强。若M1-M2增速差上升,说明M1增速大于M2增速,企业和居民更倾向持有活期存款,可用于投资的钱变多,更多资金可以流入股市,市场流动性就会更加宽裕,但是活钱变多易导致资产泡沫和通货膨胀产生,所以M1和M2剪刀差上行至高点后往往会伴随加息和货币紧缩的周期;而当M1-M2增速差下降,意味着M2增速大于M1增速,企业和居民对未来经济不看好,认为当前投资机会有限,倾向于将资金沉淀下来,经济处于下行趋势,此时央行往往会采取宽松的货币政策,如通过降息等方式提高流动性,刺激经济,而此时便是宏观流动性拐点。如图34所示,M1和M2的剪刀差与沪深300指数呈现较为同步的相关关系,秩相关系数达0.31。
从M1和M2剪刀差的历史分位数来看,结论更加清晰:当M1和M2剪刀差的历史分位值较低(如低于20%)时,往往预示宏观流动性拐点,股市即将触底反弹,如2009年初、2014年底、2018年底以及2022年4月底,这些时点均为大牛市或阶段性反弹的起点。因而,可以基于M1和M2剪刀差的历史分位值构建择时策略:若剪刀差指标低于阈值,发出看多信号,反之发出看空信号。样本内测试结果显示当阈值为20%时,择时收益最高,故后面我们以20%作为判断市场底部的阈值对Ita-DTW择时策略进行优化。
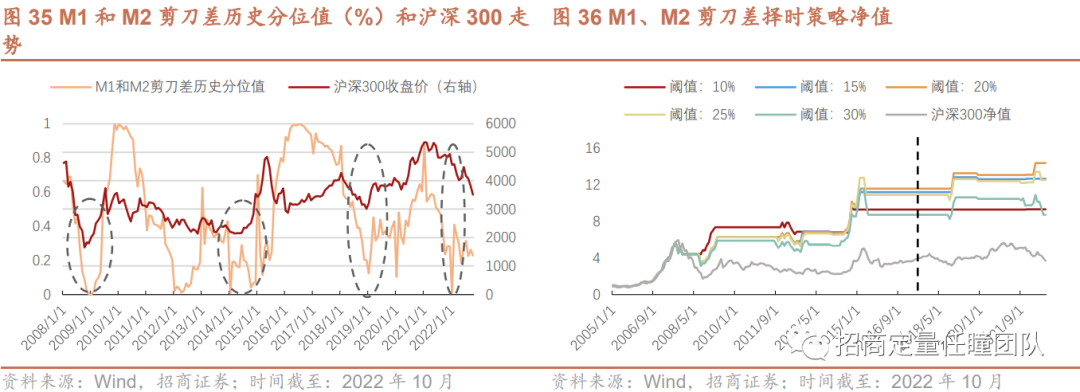
2.叠加宏观流动性指标的Macro-Ita-DTW择时策略表现
叠加M1和M2剪刀差指标后,Macro-Ita-DTW择时策略表现进一步提升。样本内年化收益提升至16.29%,胜率提升至57.57%;样本外年化收益提升至9.36%,胜率提升至53.97%,盈亏比有所改善,样本外回撤约20.29%。策略换手率亦有所下降,年均择时次数下降至9次左右。
从分年度表现来看,Macro-Ita-DTW择时策略在样本内外各年份均较为稳健,全样本中16年有14年跑赢指数,年度回撤和波动率也基本均低于指数。
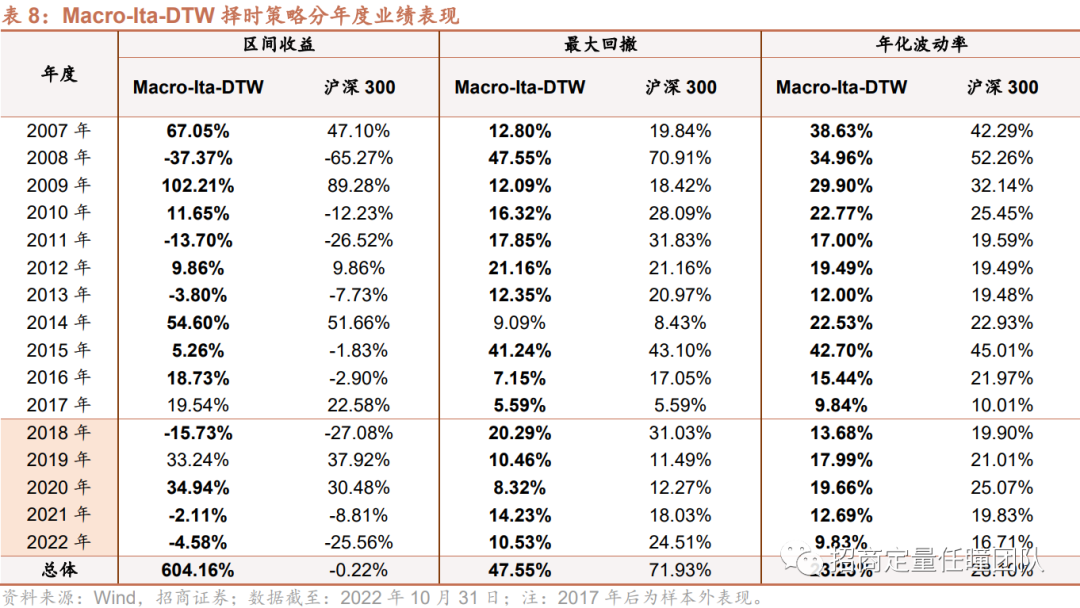
另外,我们也测试了Macro-Ita-DTW算法在日频择时上的效果,可以发现Macro-Ita-DTW在日度择时上表现出色,样本内年化收益19.08%,胜率54.83%,盈亏比1.20,样本外年化收益12.36%,胜率53.37%,盈亏比1.24,且全样本最大回撤、夏普比率等均显著优于指数。
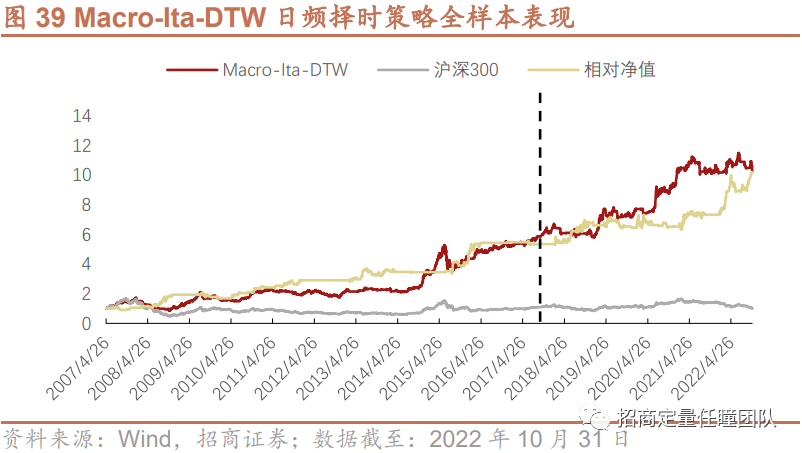
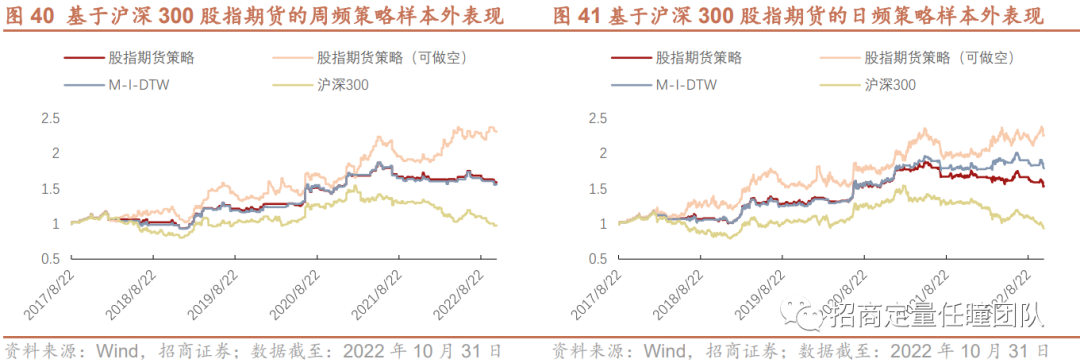
此外,以沪深300股指期货为交易标的考察Macro-Ita-DTW择时策略在样本外的实际交易表现,可以发现,周频策略的实际交易表现与模拟表现相当,年化收益均近10%,最大回撤约20%,可做空的周频股指期货交易策略年化收益提升至18.20%;日频交易策略由于交易费用原因年化收益相对模拟表现有所下降,约9%,可做空的日频股指期货交易策略年化收益约17.67%。
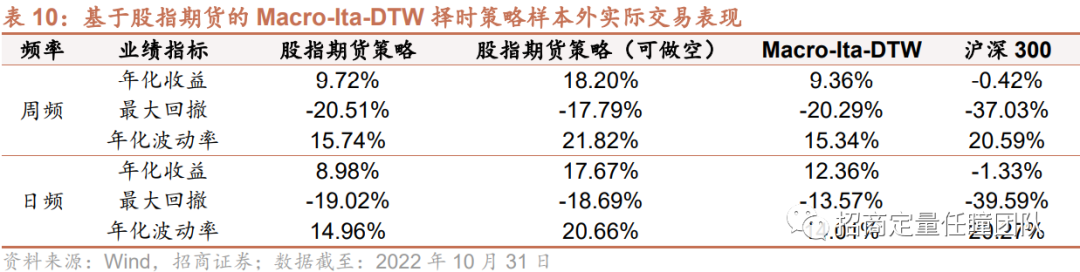
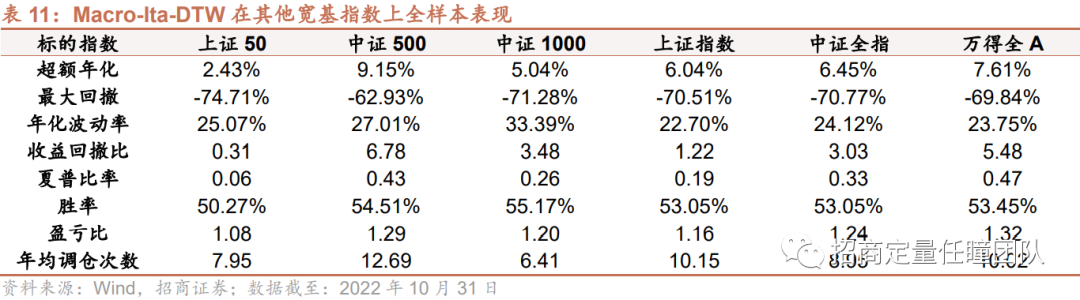
3.Macro-Ita-DTW择时策略在其他宽基指数上的表现
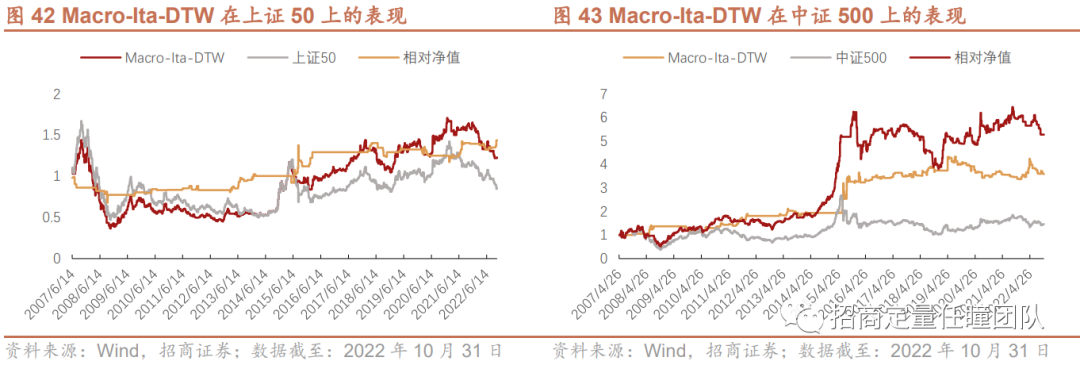
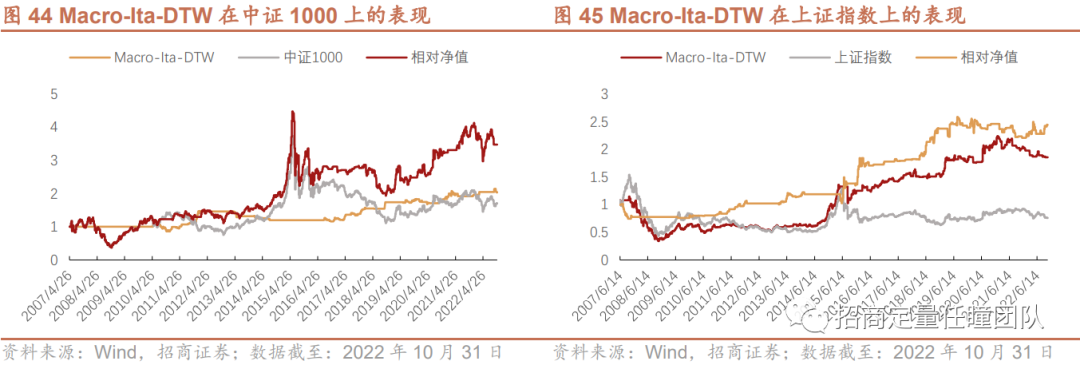
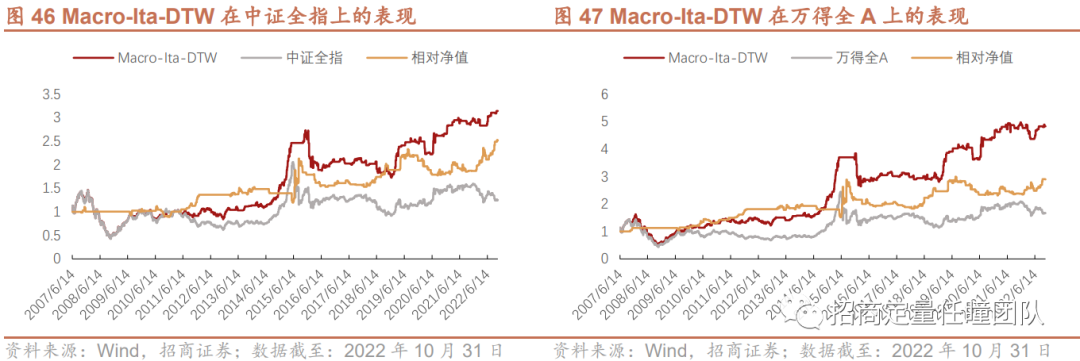
最后,我们也应用Macro-Ita-DTW择时策略分别在上证50、中证500、中证1000、中证全指等宽基指数上进行实证分析,发现也能获得较好的择时效果。
总结与讨论
本文基于改进的DTW算法,在传统DTW算法基础上对弯曲路径施加约束条件,并应用于指数择时。实证结果显示,基于Ita-DTW算法的沪深300择时策略样本内年化收益12.72%,胜率56.77%,盈亏比1.33,样本外年化收益8.33%,胜率53.57%,盈亏比1.36,且回撤显著低于标的指数,整体表现相对传统DTW择时策略有显著提升。
此外,本文叠加宏观流动性指标M1和M2剪刀差对Ita-DTW择时策略进行优化改进,Macro-Ita-DTW择时策略样本内年化收益16.29%,胜率57.57%,盈亏比1.37,样本外年化收益9.36%,胜率53.97%,盈亏比1.39,回撤和波动水平较小,样本内外表现相对Ita-DTW择时策略均有一定改善,且分年度表现也十分稳定。
最后,本文将Macro-Ita-DTW择时策略应用在其他宽基指数上,发现在其他指数上也能取得较好的效果。
展望未来,可以放松终点条件,同时考察不同长度的时间序列,从而减少模型参数(时间序列长度参数l),增强泛化能力;另外,亦可将本文提出的改进DTW算法应用于行业或风格指数以及个股,构建行业/风格轮动策略或选股策略。
重要申明
风险提示
本报告仅作为投资参考,基金过往业绩并不预示其未来表现,亦不构成投资收益的保证或投资建议。
本文选自招商证券定量研究团队的报告《引入宏观维度的改进DTW算法在择时策略上的应用——技术择时系列探索》(2023年2月21日发布),模型策略细节以报告为准。
分析师承诺
本研究报告的每一位证券分析师,在此申明,本报告清晰、准确地反映了分析师本人的研究观点。本人薪酬的任何部分过去不曾与、现在不与,未来也将不会与本报告中的具体推荐或观点直接或间接相关。
本报告分析师
任 瞳 SAC职业证书编号:S1090519080004
周靖明 SAC职业证书编号:S1090519080007
罗星辰 SAC职业证书编号:S1090522070001
特别提示
本公众号不是招商证券股份有限公司(下称“招商证券”)研究报告的发布平台。本公众号只是转发招商证券已发布研究报告的部分观点,订阅者若使用本公众号所载资料,有可能会因缺乏对完整报告的了解或缺乏相关的解读而对资料中的关键假设、评级、目标价等内容产生理解上的歧义。
本公众号所载信息、意见不构成所述证券或金融工具买卖的出价或征价,评级、目标价、估值、盈利预测等分析判断亦不构成对具体证券或金融工具在具体价位、具体时点、具体市场表现的投资建议。该等信息、意见在任何时候均不构成对任何人的具有针对性、指导具体投资的操作意见,订阅者应当对本公众号中的信息和意见进行评估,根据自身情况自主做出投资决策并自行承担投资风险。
招商证券对本公众号所载资料的准确性、可靠性、时效性及完整性不作任何明示或暗示的保证。对依据或者使用本公众号所载资料所造成的任何后果,招商证券均不承担任何形式的责任。
本公众号所载内容仅供招商证券股份客户中的专业投资者参考,其他的任何读者在订阅本公众号前,请自行评估接收相关内容的适当性,招商证券不会因订阅本公众号的行为或者收到、阅读本公众号所载资料而视相关人员为专业投资者客户。
一般声明
本公众号仅是转发招商证券已发布报告的部分观点,所载盈利预测、目标价格、评级、估值等观点的给予是基于一系列的假设和前提条件,订阅者只有在了解相关报告中的全部信息基础上,才可能对相关观点形成比较全面的认识。如欲了解完整观点,应参见招商证券网站(http://www.cmschina.com/yf.html)所载完整报告。
本公众号所载资料较之招商证券正式发布的报告存在延时转发的情况,并有可能因报告发布日之后的情势或其他因素的变更而不再准确或失效。本资料所载意见、评估及预测仅为报告出具日的观点和判断。该等意见、评估及预测无需通知即可随时更改。
本公众号所载资料涉及的证券或金融工具的价格走势可能受各种因素影响,过往的表现不应作为日后表现的预示和担保。在不同时期,招商证券可能会发出与本资料所载意见、评估及预测不一致的研究报告。招商证券的销售人员、交易人员以及其他专业人士可能会依据不同的假设和标准,采用不同的分析方法而口头或书面发表与本资料意见不一致的市场评论或交易观点。
本公众号及其推送内容的版权归招商证券所有,招商证券对本公众号及其推送内容保留一切法律权利。未经招商证券事先书面许可,任何机构或个人不得以任何形式翻版、复制、刊登、转载和引用,否则由此造成的一切不良后果及法律责任由私自翻版、复制、刊登、转载和引用者承担。
本篇文章来源于微信公众号: 招商定量任瞳团队