波动率管理战略的现代化

admin10个月前 (01-20)研报1202

导读

“西学东渐”作为以往学术传播的方式之一，其在如今仍具有重要的现实意义。作为A股市场上以量化投资为研究方向的卖方金融工程团队，我们通过大量的材料阅读，去粗取精，将认为最有价值的海外文献呈现在您的面前。
作为西学东渐——海外文献系列报告第一百六十二篇，本文推荐了Junseung Bae和Ryan Poirier于2023年发表的论文《Modernizing Volatility-Managed Strategies》。
本研究的研究思路是通过缩短波动率管理策略的实施滞后时间，以小时为单位进行再平衡，从而减少交易决策的滞后性。研究通过利用更及时和更相关的日内数据来提高波动率模型的准确性，改善波动率管理策略的绩效。
本文首先回顾了现有文献中关于利用日内数据进行波动率择时策略的优势和效果。在现有研究的基础上，本文采用了一种全天异质自回归实现波动率模型（HAR-RV）对波动率进行准确建模。同时，本文还利用了两种普通最小二乘（OLS）框架，即日历法和滚动法，对已实现波动率进行建模。本文指出，市场微观结构噪声对于波动率预测的准确性至关重要。
为了验证缩短实施滞后时间的波动率管理策略的效果，本文以一组具有高流动性和充足的日内数据的ETF作为研究样本，通过创建六个假设的波动率管理策略来验证缩短实施滞后时间的策略的效果，并比较其绩效表现。研究结果表明，缩短实施滞后时间可以提高波动率模型的准确性，从而改善波动率管理策略的绩效。这对于投资者在实践中更好地应用波动率管理策略具有重要意义。

风险提示：文献中的结果均由相应作者通过历史数据统计、建模和测算完成，在政策、市场环境发生变化时模型存在失效的风险。

1、介绍

波动率是不可观测的，但其在投资管理中却有着巨大的影响。如波动率管理策略需要对波动率进行估算，以确定标的风险资产的风险敞口。近二十年来，大量波动率管理策略均采用了相同的基本结构，即借入现金并使用杠杆（支付利息）或持有现金并将其借出（收取利息），相关策略的收益与其波动率水平成反比。波动率策略的实施过程旨在捕捉金融收益序列已被证实的时间序列特征：波动的序列相关性和杠杆效应。

现有文献已经详尽阐述了波动率管理策略的优势，主要包括降低尾部风险和提高风险调整收益（Dopfel和Ramkumar, 2013; Moreira和Muir, 2017; Harvey等, 2018）。对于那些熟悉股票因子研究的投资者来说，这一点应该不足为奇。可以说，波动率管理策略是动量策略的表兄弟（Jegadeesh和Titman, 1993; Carhart, 1997）。波动率管理策略在标的资产的波动率低（或高）时，增加（或减少）对其的风险敞口。同样的，动量策略在标的资产取得正（或负）收益时，增加（或减少）对其风险敞口，而标的资产的正（或负）收益恰好对应着低（或高）波动率。

在实证中执行波动率管理策略必须考虑两个操作要素：再平衡频率和可交易性。关于再平衡频率，Perchet等(2015)阐明了每日再平衡的好处，其研究证实了夏普比率会随着再平衡频率的增加而增加，其中半年再平衡一次的夏普比率最低，其次是每月和每周，而每日再平衡一次的夏普比率最高，其认为每日再平衡之所以更优越，是因为再平衡日期之间的收益分布更偏向正态分布，而正态分布是波动率管理策略成功的关键特征。

可交易性是一个有趣的权衡问题。我们暂且假设当且仅当投资者获取了所有先验信息时，可以完美预测次日的波动率水平。Hallerbach(2012)阐明了完美预测波动率能提高策略的夏普比率，但这是不可交易的，因为在波动率估计和执行相应指令之间必须有一定的时间间隔（即本文阐述的滞后期），无论这个时间间隔有多小。按照行业标准，投资者可以在前一天收盘后估计波动率，并在其后的一天内有一整天的时间来执行交易。这种情况下，投资者牺牲了一整天的时间，以换取足够的时间来执行订单，这将导致其在执行订单时无法掌握所有历史信息，也就无法准确预测次日的波动率，导致策略的夏普比率受限。

对于给定的再平衡频率，只有一种方法可以提高波动率管理策略的绩效表现——提高波动率模型的准确性（Hallerbach, 2012）。而模型的准确性可以通过模型设定和执行操作滞后性两种方式实现。

关于前者，Andersen等(2001a, 2001b)以及Barndorff-Nielsen和Shephard (2002a, 2002b)等人记录了盘中已实现波动率模型¹相对于传统的收盘到收盘模型（如移动加权平均线）的卓越预测能力，即通过寻找更好的模型设定来提高预测准确性。关于后者，我们也可以通过减少执行滞后期来提高模型性能。正如后文讨论的那样，减少执行滞后期本身并没有什么作用，但缩短波动率估计和执行之间的时间间隔可以在预测模型中纳入更多的最新信息，从而提高预测的准确性。直观地说，预测一年后一天的波动率（即较长的执行滞后期）要比预测第二天的波动率（即较短的执行滞后期）或后一小时的波动率更难，一年内可能会发生许多模型没有纳入考量的因素。两者在实践中都是可行的，也是投资者的兴趣所在；不过，后者可能比前者更容易实现，也是本文的重点。

本文讨论了盘中再平衡波动性管理策略的含义、操作风险和好处，对现有文献进行了补充。²换句话说，本文的目标是通过将实施滞后期从一整天缩短到仅仅几个小时，来减少前文所述的“权衡”的影响。随着交易基础策略的改进，缩短实施滞后期的波动率管理策略将变得更加可行。

通过日内数据纳入更多最新和相关的信息是一个合乎逻辑的研究起点。这一研究尽管现阶段对机构投资者的实施可行性在逐步提升，但它在投资管理领域其它部分的渗透速度仍很慢。此外，现有文献尚未对这一策略的实施流程框架进行详细阐述，本文旨在填补这一空白。

¹已实现波动率是一个不断发展的研究领域，其使用较高频率的盘中数据来计算波动率估计值。

²当日再平衡有多种含义，此处指投资者决定在当日再平衡其投资组合，而不是在当日实际执行交易。

2、波动率建模

利用盘中数据制定波动率择时策略并不是一个新颖的想法。如Fleming、Kirby和Ostdiek(2003)认为，投资者应该愿意支付50到200个基点的费用，以获得在波动率择时均值方差策略中使用日内数据所带来的更好表现。此外，Liu(2009)、Hautsch等(2015)以及Almany等(2020)都证明了在投资组合选择框架中整合日内数据的好处。最后，由于已实现波动率具有一致性，Poirier(2021)阐述了将日内数据纳入波动率管理策略将如何影响期权定价。

准确预测波动率的模型可能错综复杂，本文首先简要定义用于衡量收益的符号和日内波动率模型。根据Corsi(2009)和Hansen等(2005)，我们采用全天异质自回归已实现波动率（HAR-RV）模型¹。同时，我们还借鉴了Pascalau和Poirier(2021)的研究成果，其记录了两个普通的最小二乘法(OLS)框架，日历法和滚动²，用于对已实现波动率进行建模。市场微观结构噪声会显著影响已实现波动率的估计值。尽管Liu、Patton和Sheppard(2015)认为5分钟收益率是最佳的，但Bandi和Russell(2008)建议使用更粗略的15到20分钟的收益率来保持已实现波动率的统计一致性。

³HAR-RV模型由Corsi(2009)提出。该模型使用简单的OLS模型对波动率进行建模，并假定各种投资者(包括日内交易者与长期投资者)对预测的贡献不同。

⁴日历法将盘中数据汇总到交易日；滚动法则简单地获取连续数据，而不管盘中收益是否来自同一交易日。后者使投资者能够预测任何给定时间戳的远期波动率。

⁵价格序列的基本随机假设不在本文讨论范围之内。

⁶根据Bollerslev等(2018)的研究，只需将隔夜收益率的平方与盘中收益率的平方之和相加，就能与其他更复杂的方法一样有效。

3、波动率管理策略（重新）设计

3.1

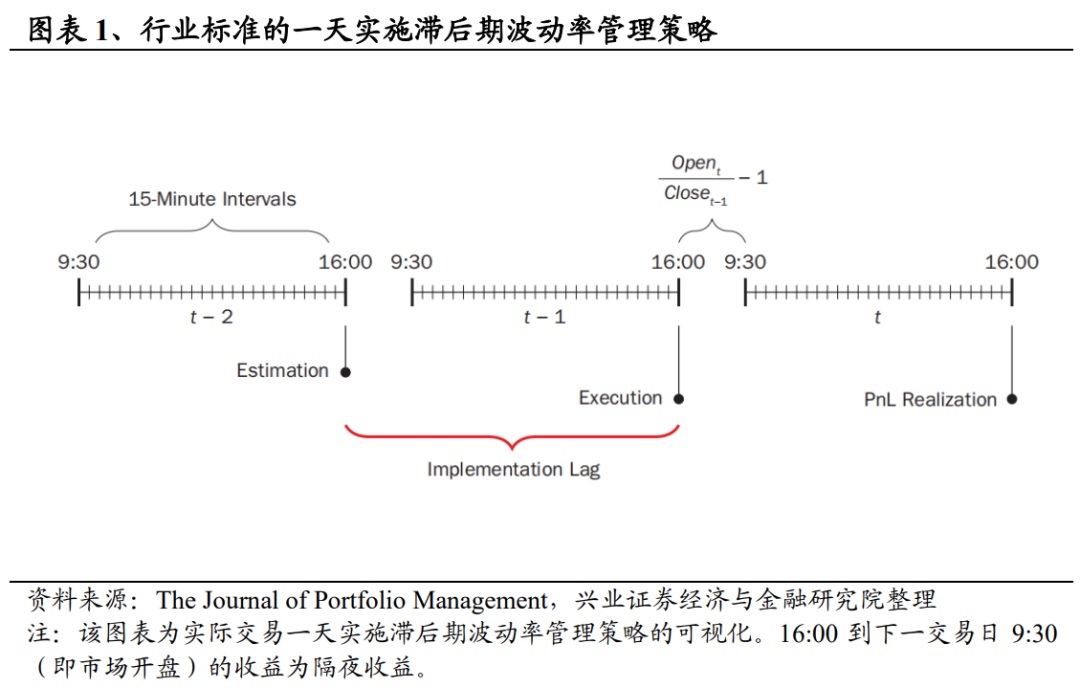
行业标准波动率管理策略

3.2

本文提出的改进波动率管理策略

在其他条件相同的情况下，执行台通常偏好更长的执行滞后期。长滞后期为其提供了充足的时间以检查交易，防止因计算机故障或数据输入等原因造成错误的盈利或亏损（这与其说是技术或实际交易限制，不如说是操作风险）。鉴于公司可以在几毫秒内对证券进行定价和交易，一整天的策略执行时间可能不是最佳选择，较长的执行滞后期实际上忽略了一部分对波动率估计至关重要的信息。用更多的最新信息来估计波动率会带来积极的好处，因为最新信息的预测能力更强，预测准确性更高。

图表2举例说明了以较短滞后期进行波动率管理策略交易的必要步骤，整体框架与图表1相同，只是缩短了估计与执行之间的时间。这个例子要求在执行的当天15:00确定波动率的估计值，即存在一小时的滞后期。但理论上，估算可以在执行前的任何时间进行，因此15:00只是众多例子中的一个。尽管执行滞后时间较短，但该策略仍在收盘时执行订单。这意味着本文提出的策略与行业标准策略的交易成本相同，且都面临当天收盘交易的买卖价差。

完全在收盘时生成的波动率估计值⁷从t-2日收盘到t-1日15:00间没有纳入新的信息以更新对波动率的估计值，因此与本文提出的策略相关性较低。本文建议的缩短滞后期策略采用式2提供的t-1日15:00的估算波动率。

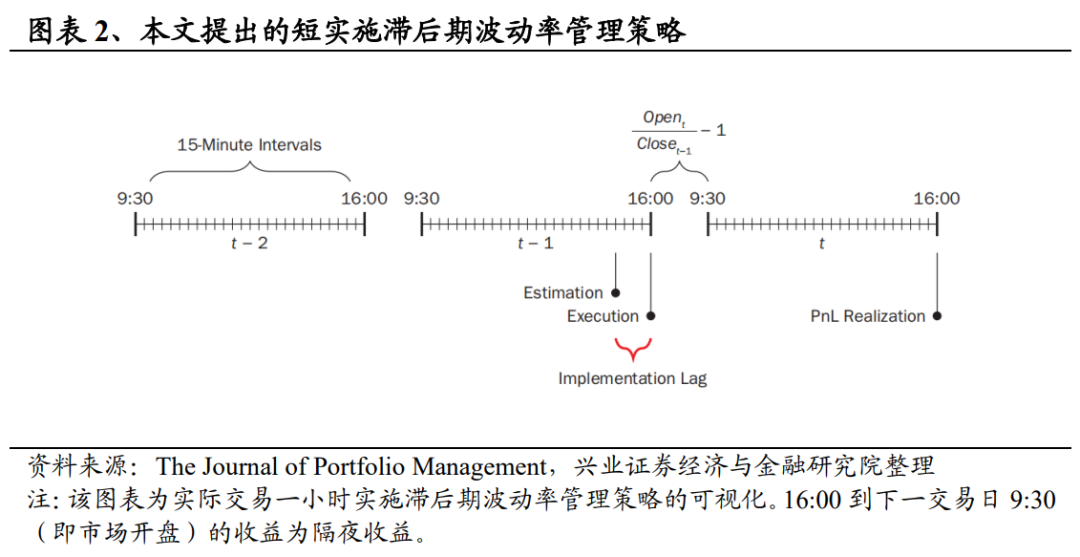
⁷行业标准波动率模型使用的是指数收盘价加权移动平均模型。

4、实证分析

4.1

数据和方法

自1993年首只SPDR S&P 500 ETF Trust(SPY)推出以来，ETF产品备受市场关注。现阶段，ETF已经成为一种能够充分发挥交易价值的工具，使交易者和资产配置者能够大规模有效地实施各种策略。与此同时，ETF还可以作为充分的价格发现工具。Wallace、Kalev和Lian(2019)指出，在价格发现方面，SPY已经与E-mini期货不相上下。出于这一考量，本文的研究对象仅包括ETF，而不包括期货的日内价格数据。

下表重点介绍了本文研究的标的资产，相关标的覆盖了可交易市场的很大一部分。如SPY、MDY和IWM大约涵盖了市值排名前3000位的证券⁸，QQQ则涵盖了全市场以科技为重点的热门股票；除此之外，EFA还涵盖了国际市场。

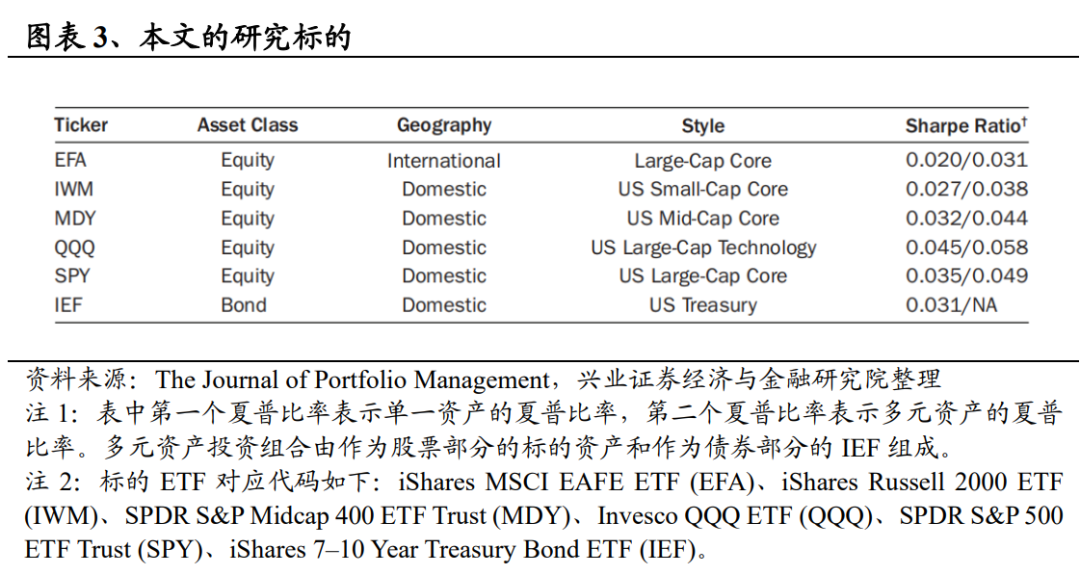
出于众多因素的考量，本文将研究范围限制在以上标的。首先，尽管盘中数据已成为主流数据，但其仍不像收盘数据那样可以免费获取¹⁰，数据限制会对未来研究的可复制性造成一定的障碍。其次，交易成本对任何策略都至关重要，本文选定的标的资产都是流动性极高的证券，允许规模庞大的投资者以最小的价格影响和成本进行交易，同时，相关标的均配置了众多相关的延伸产品，包括ETF、期货、掉期甚至复制，可以提供成本效益；而其他资产或定制的投资组合(如因子投资组合¹¹)的可交易性相对较差，对投资者来说实用性也较低。第三，尽管盘中交易执行能力在不断增长，但大多数机构的交易/风险系统只能满足(大市值、流动性好的)股票的日内交易。目前，一些机构已经建立了美国国债相关功能，但除此之外的功能纯属理论，实际用途有限。最后，对于规模更大、流动性更强的标的而言，其盘中数据通常更为可靠，即数据的信噪比更高(Ait-Sahalia和Yu, 2009)。鉴于盘中数据对波动率预测至关重要，而且更准确的预测会带来更高的夏普比率，本文只关注那些有足够盘中数据的标的。

为了实证说明本文提出的滞后缩短波动率管理策略的优势，我们创建了六个假设的波动率管理策略。策略起始日期为2004年2月5日，截止日期为2021年12月30日。¹²本文通过彭博社获取每日开盘和收盘数据，通过芝加哥期权交易所(CBOE)的Livevol数据源获取盘中柱状图数据。

在实证中，本文的每个策略都以5%的恒定波动率水平（基于式4）为目标；需要说明的是，本文的结论并不会因为σ^target的其他值（如10%或15%）而改变。此外，本文还用式3计算了基准策略，基准收益为r_t^scaled；本文提出的策略收益为r_t,T^scaled，其中T为10:00, 11:00, 12:00, 13:00, 14:00, 15:00（本文将16:00排除在外，因为此时执行滞后期为0小时，不具备交易可行性）。我们重点关注每小时最高点的表现统计，原因有二：首先，本文的研究并不是高频交易策略，因此额外的15分钟收益不太可能显著改变研究结果；其次，这减少了所需的假设检验次数，从而大大降低了多重假设检验的必要性。

大多数波动率管理策略都是应用于单一资产的纯股票投资组合，这在文献中通常表现为缩放宽基投资组合（即标准普尔500指数或期货）或因子投资组合（如Fama和French(1993)的投资组合）的收益。一般来说，没有必要将波动率管理框架应用于债券投资组合，债券的波动率已经很低了。此外，Harvey等(2018)和Perchet等(2015)分别发现了固定收益资产不存在杠杆效应和波动率集群，而这两点恰好是支撑波动率管理策略的两个关键要素。因此，我们没有报告IEF的单一资产投资组合表现，而是将IEF与每只股票ETF结合，组成了一个等权重的多资产投资组合（有关多资产策略的更多信息请参阅附录）。

⁸不同的指数提供商有不同的市值指数编制方法。也就是说，SPY大约跟踪前500家最大的公司，MDY大约跟踪其后400家公司(即501-900家)，IWM大约跟踪去掉1000家最大的公司后的2000家最大的公司(即1001-3000家)。

⁹我们将EEM等其他流行的国际ETF排除在外，因为目前还不清楚新兴市场是否表现出杠杆效应。

¹⁰由于数据共享的规定，我们无法像Heber等(2009)那样开放基础数据。

¹¹因子投资组合一般都有一个空头部分，通常包括小盘股证券，这些股票的交易和卖空成本较高。

¹²2004年之前的日内数据较难获取，数据可靠性也较低。本文的数据实际上从2004年1月2日开始，但HAR-RV成分需要按月回溯。

4.2

动机

4.3

夏普比率

即式3和式4的平均收益除以标准差¹³。

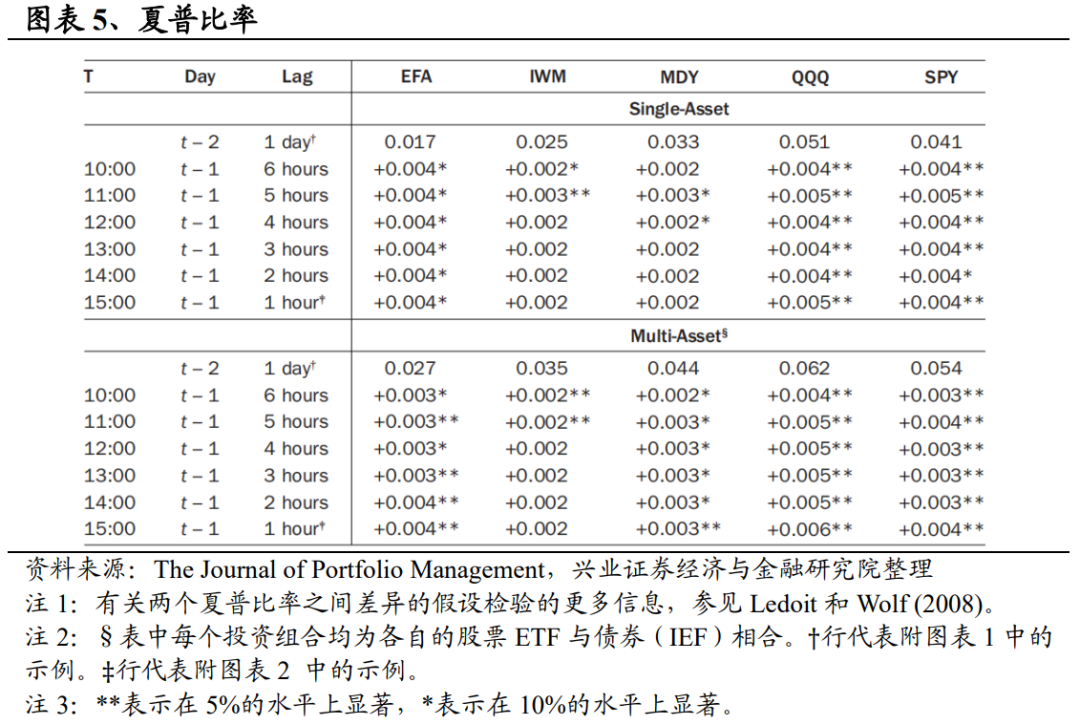
图表5第一行列出了标准的一日滞后模型（即式3）的夏普比率。随后各行计算的是在策略执行的同一天产生估算值的六种策略的相对差异（即式4）。对于六种策略中的每一种策略，我们都要检验零假设H₀^LW:SR=SR_T(见Ledoit和Wolf，2008)。结果以*表示，代表统计显著性。

对于规模最大、流动性最好的底层资产QQQ和SPY以及国际EFA，使用本文提出的波动率管理策略与基准相比，在统计上始终具有更高的夏普比率，且在单一资产和多元资产中均成立的。我们提出的波动率计算框架对多元资产配置下的MDY也有显著效果。在以上情况下，本文构造模型产生的夏普比率比行业标准模型高出+0.002（MDY，多资产）至+0.006（QQQ，多资产）；其余情况下（IWM，单一资产；MDY，单一资产；IWM，多资产）的结果尚无定论。

一般来说，对于给定的标的资产和资产配置，每小时最高点的夏普比率仅略有不同，差异大致在±0.001。尽管如此，我们还是倾向于最大限度地利用可用时间来确认订单的完整性。换句话说，如果在执行当天的15:00与10:00之间交付订单没有额外的好处，那么在其他条件相同的情况下，我们宁愿选择10:00。在此背景下，我们检验零假设H₀^WYY:SR=SR_10:00=SR_11:00=SR_12:00=SR_13:00=SR_14:00=SR_15:00(AlexanderWright等,2014)。对于所有10个组合（即5个单一资产检验和5个多资产假设检验），我们都未能在10%的水平上拒绝零假设。这一结果表明，本文的模型只需包含隔夜收益率就足够了，投资者不必担心需要等待当日收盘结果再执行订单。

H₀^LW和H₀^WYY的结果在单一资产IWM、单一资产MDY和多资产IWM中略有冲突。例如，对于单一资产IWM，H₀^LW表明10:00和11:00的波动率是唯一与基线有统计差异的指标；然而，H₀^WYY表明，本文构造的六种模型的夏普比率没有统计差异（似乎两者都不可能成立）。因此，我们保守的认为本文提出的方法并没有为单一资产IWM、单一资产MDY和多资产IWM提供统计上显著的优势。

以上关于IWM和MDY可能缺乏统计意义的结果并不令人沮丧，许多学术研究发现，统计显著性通常出现在难以交易的资产上，这意味着研究结果并不实用。而本文发现的情况恰恰相反，最容易交易的资产表现出统计意义，这对策略的实际执行来说是件好事。IWM和MDY绝不是难以交易的资产，然而就交易美元价值而言，SPY和QQQ占据了主导地位：SPY每日交易的总名义价值大约是IWM的6倍、是MDY的60倍；QQQ的价值约为其一半，即是IWM的3倍、MDY的30倍。此外，一般来说SPY或QQQ是投资美国市场的首选资产，因为它们具有更广泛的认可度。

¹³根据Lo(2002)的研究成果，本文并未通过除以√252将估计误差将其转换为年度指标。

4.4

交易成本

Carroll等(2017)建议计算一个策略收益被抵消的盈亏平衡成本。虽然在文中没有报告，但本文也研究了更高的交易成本，最高达200个基点，以确定这一盈亏平衡成本。随着交易成本从1个基点增加到200个基点，图表5中本文提出的策略的绩效优势会越来越明显，即盈亏平衡成本不在1到200个基点之间。这是因为本文提出的方法在改变杠杆风险敞口的时间和程度上更有效，能更好地捕捉未来收益。鉴于本文的研究标的都是美国规模最大、流动性最强的证券，而且无论从哪个角度看，200个基点都是不现实的，因此简单地假设2个基点是一个保守的假设，尤其是在交易成本较高的情况下，业绩差距会更大。

图表6记录了实施单资产SPY案例的标准一天滞后策略的年度交易成本和我们提出的一小时滞后策略的年度交易成本，即TC_t(或TC_t')的最后252个日观测值之和，每个观测值都衡量了执行当天交易的成本。

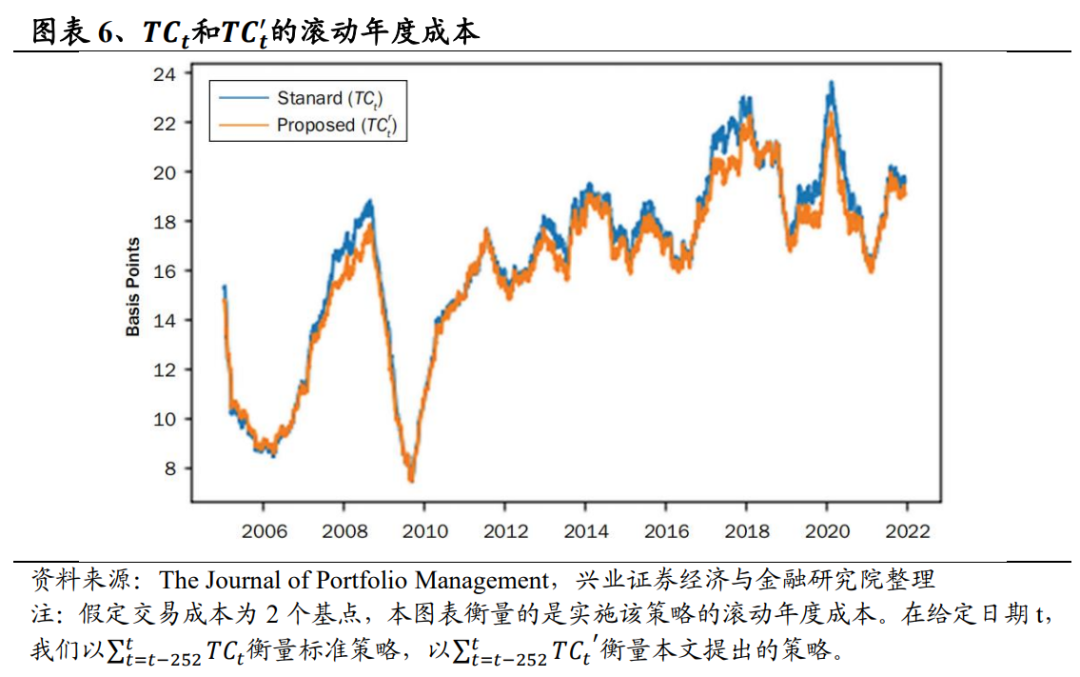
虽然本文构造策略的交易成本略低，但显然，两者遵循类似的路径，这意味着策略的实现成本大致相同。同时，除SPY外，其他标的成本的时间序列也呈现类似的趋势。

4.5

经济效益（效用）

投资者希望知道本文提出的策略对他们来说值多少钱。换句话说，投资者愿意支付多少钱来使用这种策略？Bollerslev等(2018)开发了一个框架，用于在假设投资者采用波动率择时策略的情况下衡量已实现效用，恰好符合本文研究的情况。

因此，本文利用这一框架来测试本文提出的短滞后期波动率管理策略的经济效用。目前为止，所有策略假设的目标波动率均为5%，这个目标波动率并不影响预期效用的计算；然而，我们必须对投资者的风险厌恶程度(γ)做出假设。参考Bollerslev等(2018)的研究，我们设定γ=2。

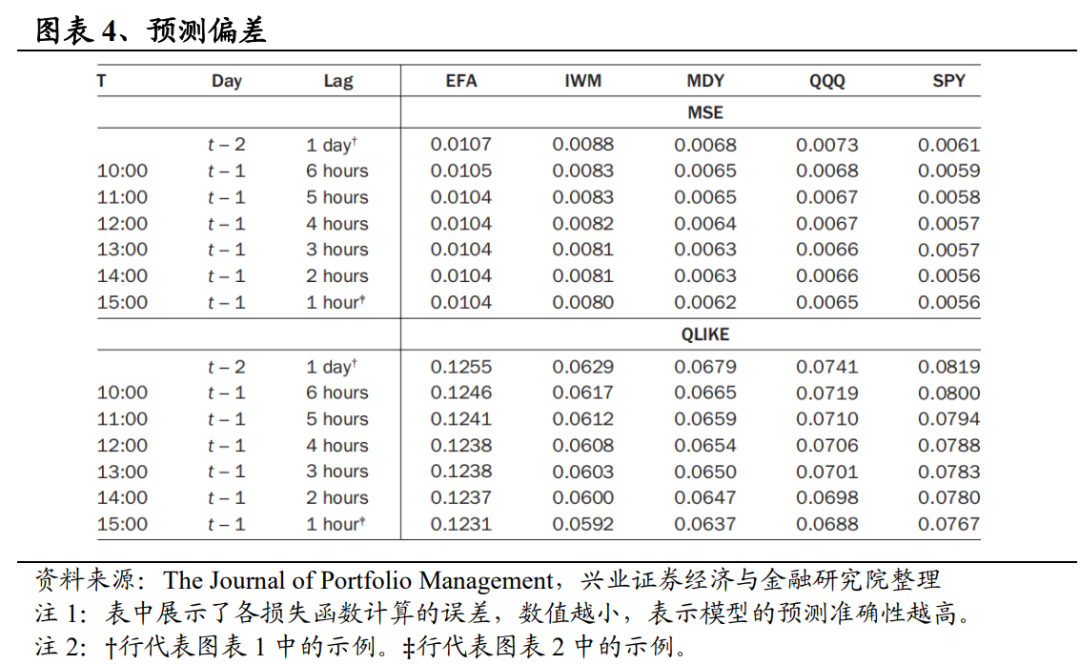
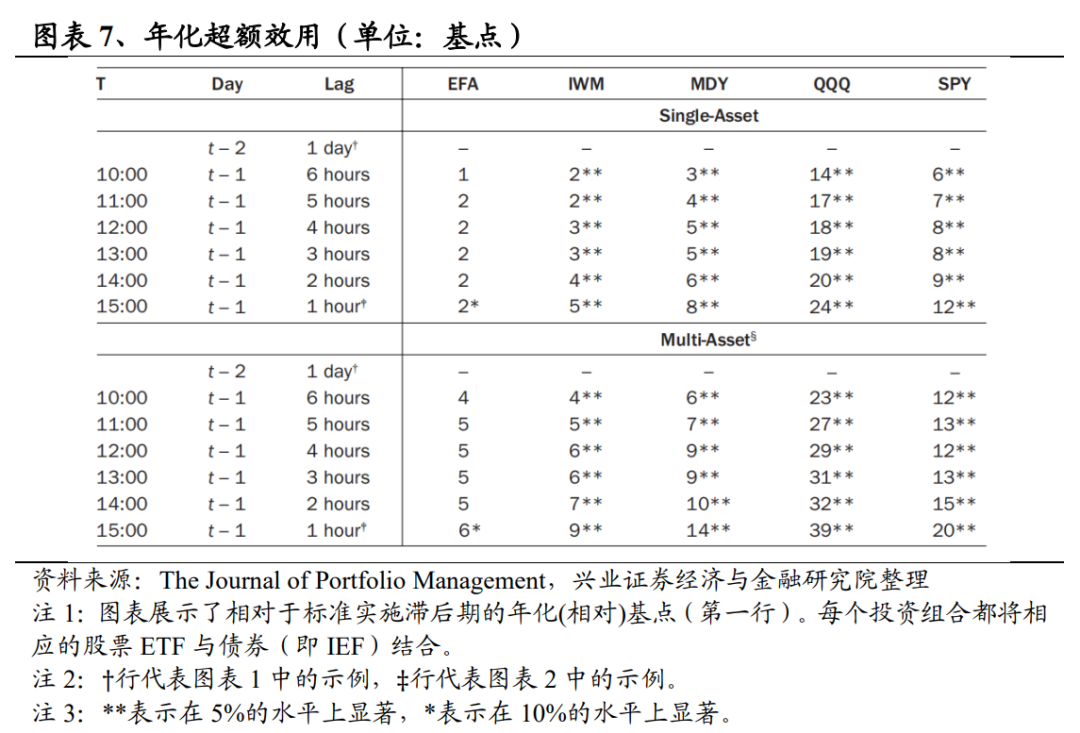
图表7以年化基点为单位说明了策略相对于基准模型的超额效用。初看之下，我们发现了几个问题：首先，我们提出的框架为（相对）流动性较高的资产，即标准普尔500指数和纳斯达克100指数，带来了最大的收益。事实上，仅考虑美国国内指数产品，本文效率排序结果的从高到低与这些ETF的加权平均市值相同：QQQ（10330亿美元）、SPY（5960亿美元）、MDY（73.9亿美元）和IWM（31.7亿美元），且单资产和多资产应用的情况都是如此。其次，随着交易接近收盘，超额效用似乎会增加。这一结论在直觉上是有道理的，因为波动率预测随着时间的推移会越来越准确（见图表4）。第三，无论在什么时间进行估算，所有的美国国内底层资产与基准资产相比，超额效用均在5%的水平上显著。此外，本文提出的一小时滞后在10%的水平上为EFA提供了统计意义上的超额效用，尽管相对较小。第四，虽然IWM在美国国内ETF中排名最低，但其值在统计上是显著的，这一点在夏普比率中没有体现出来。最后，在使用IEF交易多资产投资组合与单一资产投资组合时，投资者应该愿意为本文提出的策略支付大约两倍的费用。

为了进一步凸显本文研究方法的经济意义，考虑将10亿美元分配给一个实施波动率管理策略的基金。假设该基金根据式3配置了流动性最好的美国证券SPY，且该基金确定了其在t-2时刻的交易决策，即L_t-2。换句话说，该基金使用行业标准的一天执行滞后期策略，让执行交易者有一整天的时间来执行交易。本文的结果表明，投资者应该愿意每年支付120万美元，即12个基点，以让基金经理实施一小时的执行滞后期策略。假设基金经理的交易(或风险)部门对一小时滞后感到不满，他们仍应愿意每年支付60万美元，以获得在10点而不是隔夜发送订单的能力。如果他们正在探索一种多资产SPY/IEF解决方案，那么他们应该愿意每年支付大约上述价值的两倍，即分别为200万美元和120万美元，以实施本文提出的策略框架。一般来说，γ水平越高(越低)，超额效用越低(越高)。也就是说，如果我们将风险厌恶程度提高到γ=4以使计算更加保守，我们只需按比例缩放超额效用即可。此时，每个观测值仍具有统计，但超额效用只有原来的一半，波动率管理的SPY投资者现在应该愿意支付6个基点(而非前文的12个基点) 来获取本文提出的T=15:00时的策略。

即使对γ值的估计更加保守，这些结果对投资者来说仍具有重要的经济意义。

4.6

锚定波动的能力

投资者配置波动率管理策略不仅仅是为了潜在的更高的夏普比率，他们期望这些策略能达到一定的效果，即(合理地)瞄准一定的波动率水平。对于现金-股权投资者来说，这有助于他们在大盘大规模下跌时维持投资。即使在大盘大幅缩水时，这些策略仍将保持固定的隐含波动率，从而稳定下跌幅度，使投资者有能力维持长期投资。也就是说，虽然对于现金-股权投资者来说，持续已实现波动率目标的能力并不一定是最重要的，但对于结构性投资来说具有重大意义，因为在结构性投资中，投资者实际上持有波动率管理策略的期权(Poirier, 2021)。

我们首先计算r_t^scaled以及本文提出的六个r_t,T^scaled的滚动22天年化波动率。取滚动波动分布的标准差，即为波动率的波动率。该数值越小表明策略能更稳定地达至预期的波动率目标σ^target。在为结构性投资期权定价时，这个统计量是至关重要的。波动率的分布越紧密，或者波动率的波动性越低，意味着交易商在对冲期权时的不确定性越小，因此，在其他条件相同的情况下，期权价格越低。鉴于结构性投资的投资者看多看涨期权¹⁴，其往往偏好更低的期权价格。

图表8展示了各种单一资产和多元资产策略的波动率降低情况。同样，实施滞后期较短的策略表现出更有利的特性，尤其是在单一资产情况下。本文提出的短滞后期策略可以将波动率的波动率降低4.8个基点（IWM，两小时滞后期）至8.7个基点（SPY，一小时滞后期）。

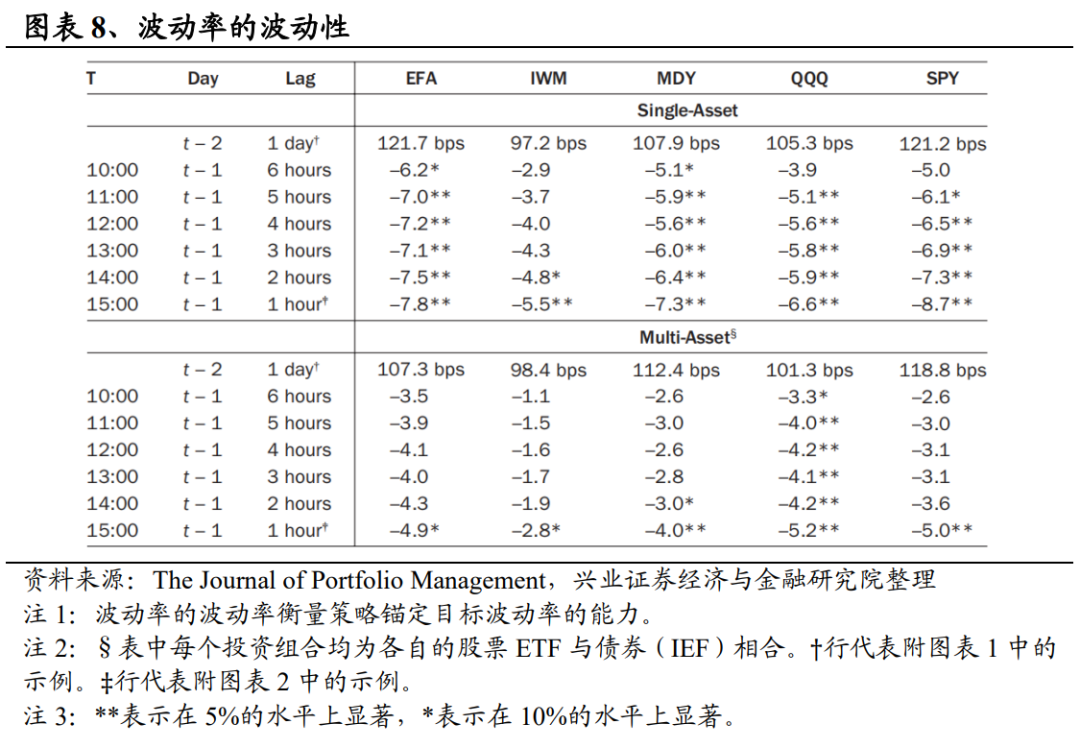
在多资产投资组合方面，本文提出的不同滞后期策略仅针对QQQ能够稳定降低其波动率的波动率；而一小时滞后期策略下，所有多资产策略波动率的波动率均显著降低，降幅从2.8个基点（IWM）到5.2个基点（QQQ）不等；此外，唯一有显著意义的是滞后期为两小时的多资产MDY。

波动率的波动率是为了减少分布中的极端情况。这对资产较少的投资组合来说相对更容易，因为分散化能提供的增益效果有限；而多资产投资组合受益于多样化，自然能稳定波动率，也因此改进模型的难度更高。

¹⁴假设投资者投资于保本票据、固定指数年金或与市场挂钩的存单，则投资者持有价内看涨期权的多头敞口。关于这种结构的更多信息，参见Poirier (2021)。

5、结论

波动率管理策略对从业者来说并不陌生，大量研究证实了这一策略的增值作用。本文提出了一种切实实施这些策略的新方法。具体来说，本文证明了波动率管理策略可以通过缩短实施滞后期来改进，从行业标准的一整天缩短到几个小时。本文通过提供一个稳健的策略实施框架，填补了学术文献中的这一空白。

本文通过三个绩效指标来验证所提出方法的优势。首先，本文考察了策略夏普比率的改善，将执行滞后期缩短至数小时可使单一资产（多资产）策略的夏普比率提高约9%（7%）。其次，本文考察了超额效用，即投资者愿意为使用本文所构造策略支付的费用，投资者在实施以标准普尔500指数（即美国大盘股）为标的的波动率管理策略时，应该愿意支付多达12个基点的费用以缩短实施滞后期。最后，本文考察了本文所构建的波动率预测框架能否更稳定地瞄准预期波动率水平，针对单一资产而言，较短的实施滞后期会降低波动率的波动性。在三项绩效指标中，不同的资产表现出不同的效益，所有策略的夏普比率都大于或等于基线，超额效用大于或等于零，波动率小于或等于基线。

学术研究在分析投资方案时必须考虑实际限制。就波动率管理策略而言，我们必须重视通过当前波动率估算头寸规模与执行订单之间的滞后性。迄今为止，估计与执行之间间隔一整天的行业标准一直是最稳健的执行方式；然而，本文证明了采用更短的滞后时间（即几小时）是更优的选择。综合来看，本文提出了一个稳健的波动率预测框架，并证实了可以通过缩短估算与执行之间的时间来提高波动率管理配置策略的绩效。

参考文献