【华安金工】基金波动率来源与基金业绩——“学海拾珠”系列之一百六十六
►主要观点
01
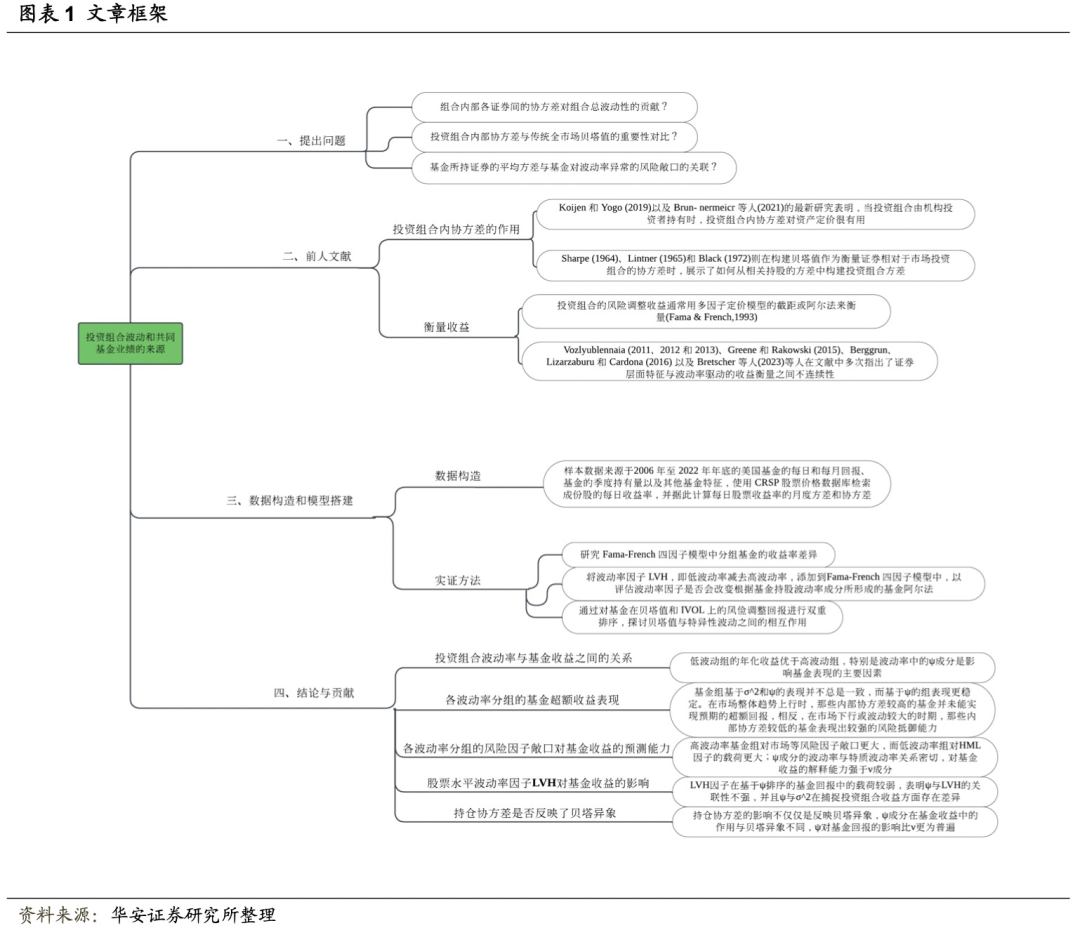
在资产定价的历史长河中,投资者和学者一直致力于解开组合收益如何反映个别证券价格的谜题。自Harry Markowitz在1952年首次提出现代投资组合理论以来,探索投资组合收益与其组成证券价格之间的复杂关系便成为了资产定价领域的核心议题。随着时间的推移,资产定价理论在不断的演进与发展中,逐渐将焦点转向对投资组合内部波动率的深入探讨。在这一过程中,经典的资产定价模型,如资本资产定价模型(CAPM)和Fama-French(1993)的三因子模型等陆续出现,这些模型试图通过分析单一证券的市场敞口——通常表示为贝塔值——来解释资产的预期收益。然而,这些模型往往忽略了组合内部各证券间的协方差对组合总波动性的贡献。虽然它们在阐释单一证券的风险和收益方面取得了显著成就,但它们在解释投资组合层面的波动性异常时有一定的局限性。这些模型通过贝塔值来强调市场风险敞口,并在金融市场理论与实践方面发挥了关键作用,但往往未能全面捕捉投资组合内部复杂的动态关系。
02
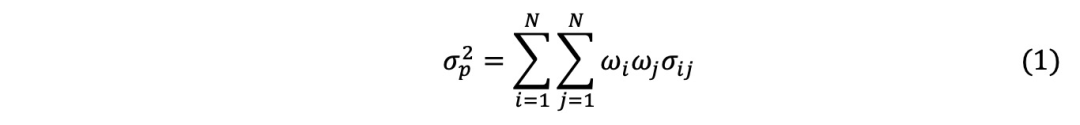
其中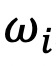 是资产i在投资组合p中的权重,
是资产i在投资组合p中的权重, 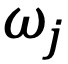 是资产j在投资组合p中的权重。
是资产j在投资组合p中的权重。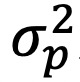 是投资组合收益的方差,
是投资组合收益的方差,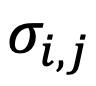 是资产i和j之间收益的协方差。为区分方差和协方差(Campbell等人,2012),等式(1)的右侧可表示为:
是资产i和j之间收益的协方差。为区分方差和协方差(Campbell等人,2012),等式(1)的右侧可表示为:
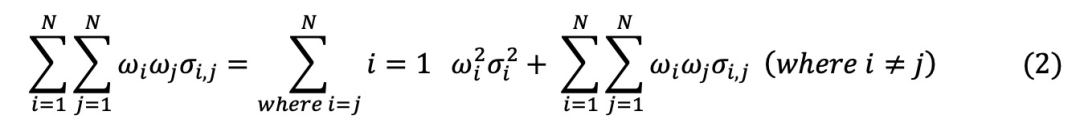
将公式(2)的第一项称为ν,第二项称为ψ。ν是成分股方差的(平方)加权平均值,构成方差-协方差矩阵的对角项。第二项ψ是所持成分股协方差的加权平均值,代表单个证券对投资组合方差的贡献。众所周知,随着投资组合持股数量的增加,ν趋近于零(Statman,1987)。鉴于分散投资的收益已为人熟知,文献将ν纳入仅作结果说明,而主要关注点是ψ。文献研究了ψ在多大程度上捕捉到了投资组合对基于波动性的异常情况的风险敞口。
从证券价格研究中心(CRSP)的基金每日数据库中计算出公式(2)的两个部分,将每个基金与其持有的成分股进行映射。通过对基金而非模拟投资组合的关注,研究现实世界中投资者和基金经理的收益在多大程度上来源于证券层面的收益波动。公式(2) 的第一部分是利用基金k持有的每种证券i日收益率计算出的每月平方加权持股方差:
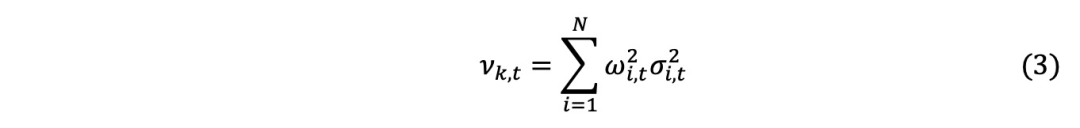
其中,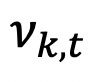 是基金k在第t个月的平均持仓方差,
是基金k在第t个月的平均持仓方差,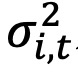 是基金k的成分股i在第t个月的方差。公式(2)中的第二部分
是基金k的成分股i在第t个月的方差。公式(2)中的第二部分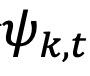 ,是通过从投资组合总波动率
,是通过从投资组合总波动率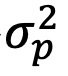 中减去平均持仓方差计算得出的:
中减去平均持仓方差计算得出的:
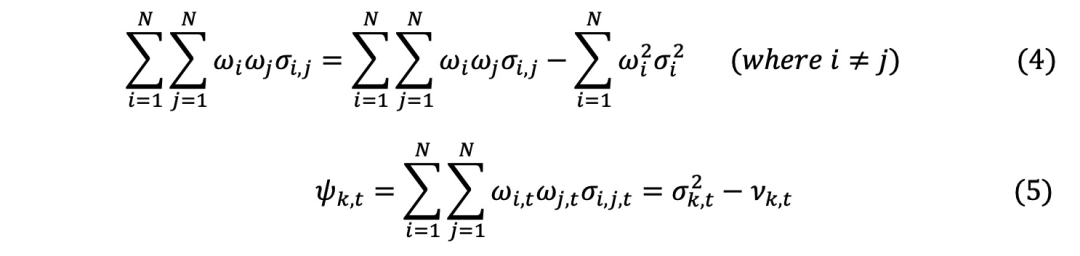
其中,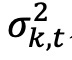 为投资组合波动率,
为投资组合波动率,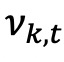 为投资组合k中证券的平均方差,
为投资组合k中证券的平均方差,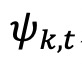 为投资组合k中证券的加权平均协方差。
为投资组合k中证券的加权平均协方差。
与贝塔系数不同的是,每种证券i对ψ的贡献是唯一的。在分析中,通过对ψ和贝塔值进行双重排序,确认了ψ和贝塔值之间的经验区别。直观地说,贝塔值是相对于市场构建的,对均衡资产定价有影响,而ψ是仅相对于投资组合中的其他股票构建的,对基金管理和收益有影响。Koijen 和 Yogo (2019)以及Brun- nermeicr 等人(2021)的最新研究表明,当投资组合由机构投资者持有时,投资组合内协方差对资产定价很有用,该研究的基金样本就是这种情况。通过仔细研究投资组合的方差来源,可以更好地理解基于波动率的回报模式。低风险或波动率异常是指低方差证券组合的表现优于高方差证券组合(Black,1972;Blitz &Van Vliet,2007;Haugen & Heins,1975) 。Blitz, Van Vliet 和 Baltussen (2019)对波动异常的研究进行了全面总结。特质波动率异常指的是投资组合所持股票的特质波动率与投资组合收益之间密切相关的负相关关系(Ang等人,2006年,Ang、Hodrick、Xing和 Zhang;2009 年;Bali、Cakici、Yan 和 Zhang,2005 年;Fu,2009 年)。Vozlyublennaia(2012)总结了有关特异波动异常的研究。贝塔异常反映了一种类似的模式,即低贝塔股票投资组合比高贝塔股票投资组合获得更高的回报 (Black、Jensen & Scholes,1972;Frazzini & Pedersen ,2014 ; Reinganum , 1981 ) LiuStambaugh和 Yuan(2018)将特异性和贝塔异常联系在一起认为贝塔异常源于贝塔与特异性波动的正相关性。关于异象与证券的关系的错误推断之所以会发生,是因为上述异象通常是在证券层面指定的,但却用投资组合回报进行了测试。Irvine 等人(2022)令人信服地证明,共同基金的收益衡量标准受到贝塔异常的强烈影响。与一样,Irvine、Kim和 Ren 也使用证券层面的风险指标来重新评估基金层面的收益。然而,Irvine、Kim和 Ren 专注于针对贝塔反常现象调整基金收益的因子模型,而文献则从更应用的角度来确定基金持仓的协方差如何转化为一般的基金回报模式。
文献的研究问题是:
问题 1: ν和ψ与基金收益有何关联?
问题 2: ν和ψ与基金面临的特异性风险有何关联?
问题 3: ν和ψ与基金受贝塔异常影响的程度有何关联?
数据来源于证券价格研究中心(CRSP)的美国共同基金数据库,样本数据来源于2006年至2022年年底的基金的每日和每月回报、基金的季度持仓以及其他基金特征,使用CRSP股票价格数据库检索成分股的每日收益率,并据此计算每日股票收益率的月度方差和协方差。为避免Evans(2010)的孵化偏差,未满一年的基金被剔除。投资组合中的证券权重采用CRSP percent_tna变量。单个基金的多个份额类别合并计算。基金至少有80%的回报数据时,纳入样本。
研究Fama-French四因子模型(Carhart,1997)中等分组基金的收益率差异,根据公式(1)、(3)和(5)中给出的每种波动率指标对基金进行分类,从而构建等分组。每月根据t月份的基金日收益方差(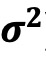 )、平均持仓方差(ν) 和平均持仓协方差(ψ)将基金分为十组。以每月每组基金的等权平均收益率作为衡量标准。按照Carhart(1997)的方法,风险调整后的收益是根据多因子模型计算出的。
)、平均持仓方差(ν) 和平均持仓协方差(ψ)将基金分为十组。以每月每组基金的等权平均收益率作为衡量标准。按照Carhart(1997)的方法,风险调整后的收益是根据多因子模型计算出的。
为了研究问题1,首先根据基金波动率的组成部分对投资组合进行分类,然后,按照 Jordan 和 Riley(2015)的过程,检验过去的基金收益波动率是否能预测未来的基金收益。不过,重点是增加:哪种波动成分能预测收益的检验:
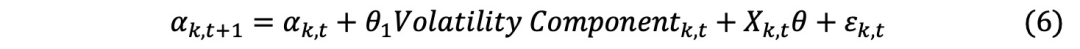
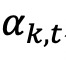 是基金k在第t个月的截距,由Fama-French四因子模型估算得出。
是基金k在第t个月的截距,由Fama-French四因子模型估算得出。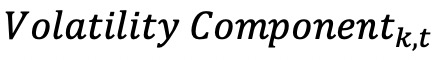 是基金k在第t个月的波动成分ψ或ν。
是基金k在第t个月的波动成分ψ或ν。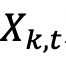 是Fama-French因子载荷矩阵,θ是Fama-French因子载荷的附加系数估计向量。波动成分和因子载荷是根据基金k在每个月的日收益率构建的。采用 Fama 和 MacBeth(1973)的方法估计公式(6)。所有变量都进行了标准化处理 (减均值除以标准差)。
是Fama-French因子载荷矩阵,θ是Fama-French因子载荷的附加系数估计向量。波动成分和因子载荷是根据基金k在每个月的日收益率构建的。采用 Fama 和 MacBeth(1973)的方法估计公式(6)。所有变量都进行了标准化处理 (减均值除以标准差)。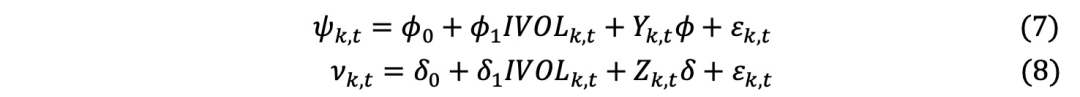
其中,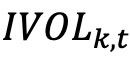 表示特质波动率,即t月份基金k的残差项的标准差,采用 Fama-French的三因子、四因子和五因子模型根据 Ang、Iodrick、Xing和 Zhang (2006和 2009)的方法从每日收益率中估算得出。Y和Z是Fama-French因子矩阵,ϕ和δ是RMRF、SML、HMB 和 UMD 因子的系数估计向量。
表示特质波动率,即t月份基金k的残差项的标准差,采用 Fama-French的三因子、四因子和五因子模型根据 Ang、Iodrick、Xing和 Zhang (2006和 2009)的方法从每日收益率中估算得出。Y和Z是Fama-French因子矩阵,ϕ和δ是RMRF、SML、HMB 和 UMD 因子的系数估计向量。
接下来,将 Jordan 和 Riley (2015)的波动率因子LVH,即低波动率减去高波动率)添加到Fama-French四因子模型中以评估波动率因子是否会改变根据基金持股波动率成分所形成的十分组的alpha推断。Jordan 和 Riley 的研究表明,加入Fama-French波动率异常风格因子后,低波动率基金的估计正收益率会消失。根据 Jordan和 Riley 的研究,构建的 LVH 因子等于前一个日历月日收益率标准差最低组股票的市值加权投资组合收益率减去最高组股票的市值加权投资组合收益率。
为了回答问题3,利用每日收益率计算出每只基金的月alpha和贝塔值。然后,通过对基金收益和基金所持股票的波动性成分进行双重分类,将基金的月度收益与贝塔系数联系起来。最后,通过对基金在贝塔值和IVOL 上的风俭调整回报进行双重排序,探讨贝塔值与特异性波动之间的相互作用。
03
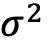 、ψ和ν排序的十分组的年化收益,没有列出最高分位组和最低分位组之间差异的t统计或p值,因为所有数据都在1%的水平上显著。算术平均收益率、几何平均收益率和方差都是根据月度收益率计算的年化指标。与 Jordan 和 Riley(2015)的研究一样,由于共同基金不能卖空,投资者不可能直接投资最高和最低十分位数之间的收益差异。低波动组和高波动组统计数据之间的差异代表了投资高波动基金而非低波动基金的机会成本。
、ψ和ν排序的十分组的年化收益,没有列出最高分位组和最低分位组之间差异的t统计或p值,因为所有数据都在1%的水平上显著。算术平均收益率、几何平均收益率和方差都是根据月度收益率计算的年化指标。与 Jordan 和 Riley(2015)的研究一样,由于共同基金不能卖空,投资者不可能直接投资最高和最低十分位数之间的收益差异。低波动组和高波动组统计数据之间的差异代表了投资高波动基金而非低波动基金的机会成本。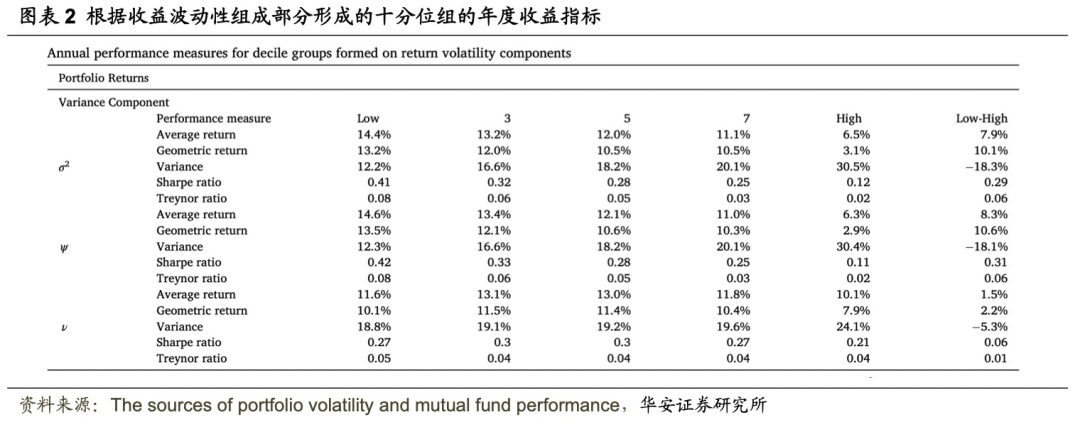
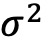 和ψ都与单调递减的收益水平相关。按ψ排序的多空组收益率差距比按
和ψ都与单调递减的收益水平相关。按ψ排序的多空组收益率差距比按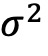 排序的更大,分别为5.60%和5.29%。按ν排序的分组收益率呈反U型,中间分组的收益最高。
排序的更大,分别为5.60%和5.29%。按ν排序的分组收益率呈反U型,中间分组的收益最高。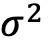 和ψ排序的组,波动率差异越大的组的收益相关性越低。对于以ν排序的分位组,收益相关性在不同的波动水平上更加不稳定,这表明组收益与ν的相关性不如与
和ψ排序的组,波动率差异越大的组的收益相关性越低。对于以ν排序的分位组,收益相关性在不同的波动水平上更加不稳定,这表明组收益与ν的相关性不如与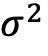 或ψ的相关性那么一致。
或ψ的相关性那么一致。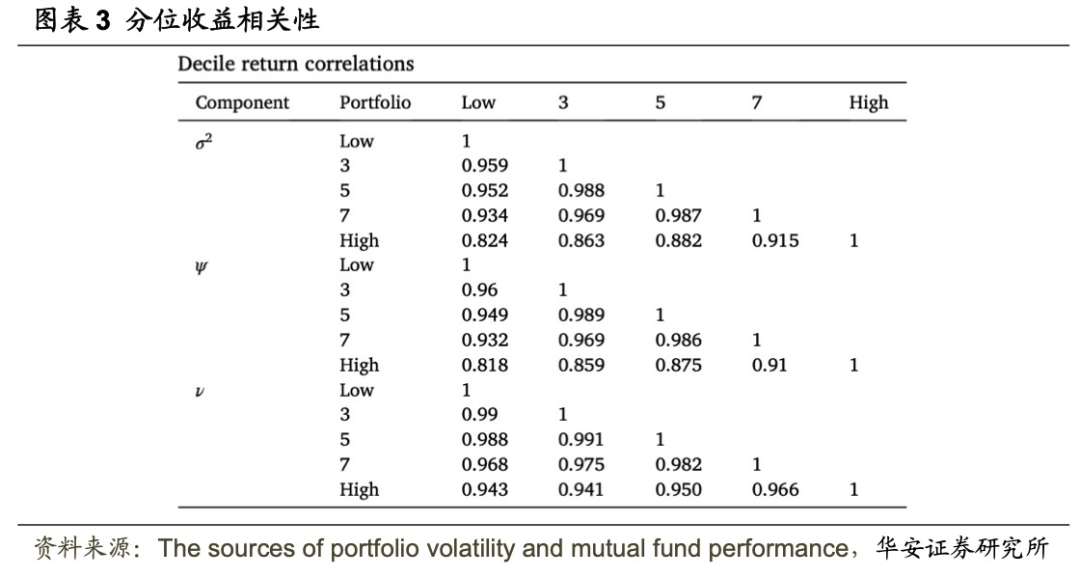
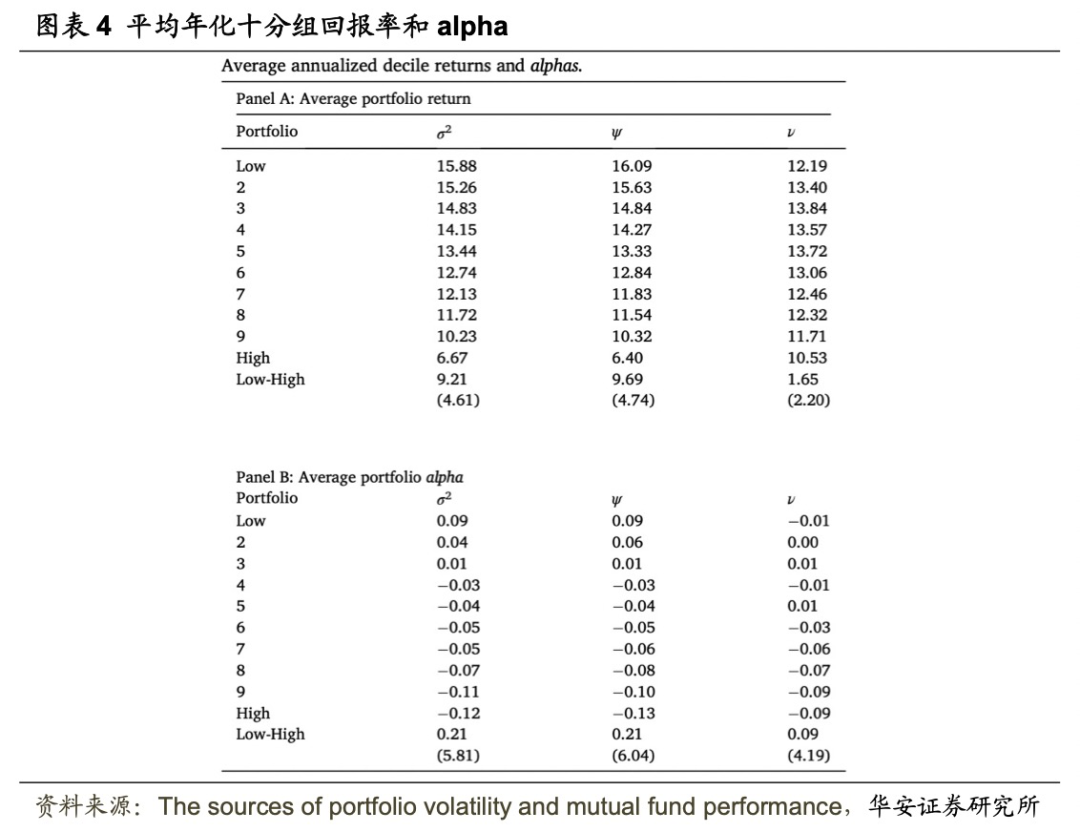
图表4展示了各个波动率分组的平均收益和Alpha,提供了更详细的证据。第一列表明,各组收益率与波动率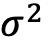 呈现单调递减。与
呈现单调递减。与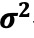 排序相比,以ψ排序的单调性更严格,顶部和底部十分位组之间的差异更大(收益率差异为 5.60%,而
排序相比,以ψ排序的单调性更严格,顶部和底部十分位组之间的差异更大(收益率差异为 5.60%,而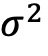 为5.29%;alpha差异为0.40,而
为5.29%;alpha差异为0.40,而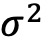 为 0.39),也更显著。根据波动率的ν分量进行的排序没有显示出单调的模式,并且最高和最低十分位之间的差异较小。总的来说,这些结果表明,波动率中的ψ成分对整体波动率模式作出主要贡献。
为 0.39),也更显著。根据波动率的ν分量进行的排序没有显示出单调的模式,并且最高和最低十分位之间的差异较小。总的来说,这些结果表明,波动率中的ψ成分对整体波动率模式作出主要贡献。
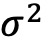 形成的十分位组的年化平均四因子alpha。为清楚起见,只列出了第一(低波动率)、第五和第十(高波动率)组。低
形成的十分位组的年化平均四因子alpha。为清楚起见,只列出了第一(低波动率)、第五和第十(高波动率)组。低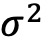 组和高
组和高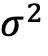 组的表现差异在不同时期并不一致。2006 年、2008 年、2011 年、2012 年、2013 年和 2021 年,高波动组的表现高于低波动组。
组的表现差异在不同时期并不一致。2006 年、2008 年、2011 年、2012 年、2013 年和 2021 年,高波动组的表现高于低波动组。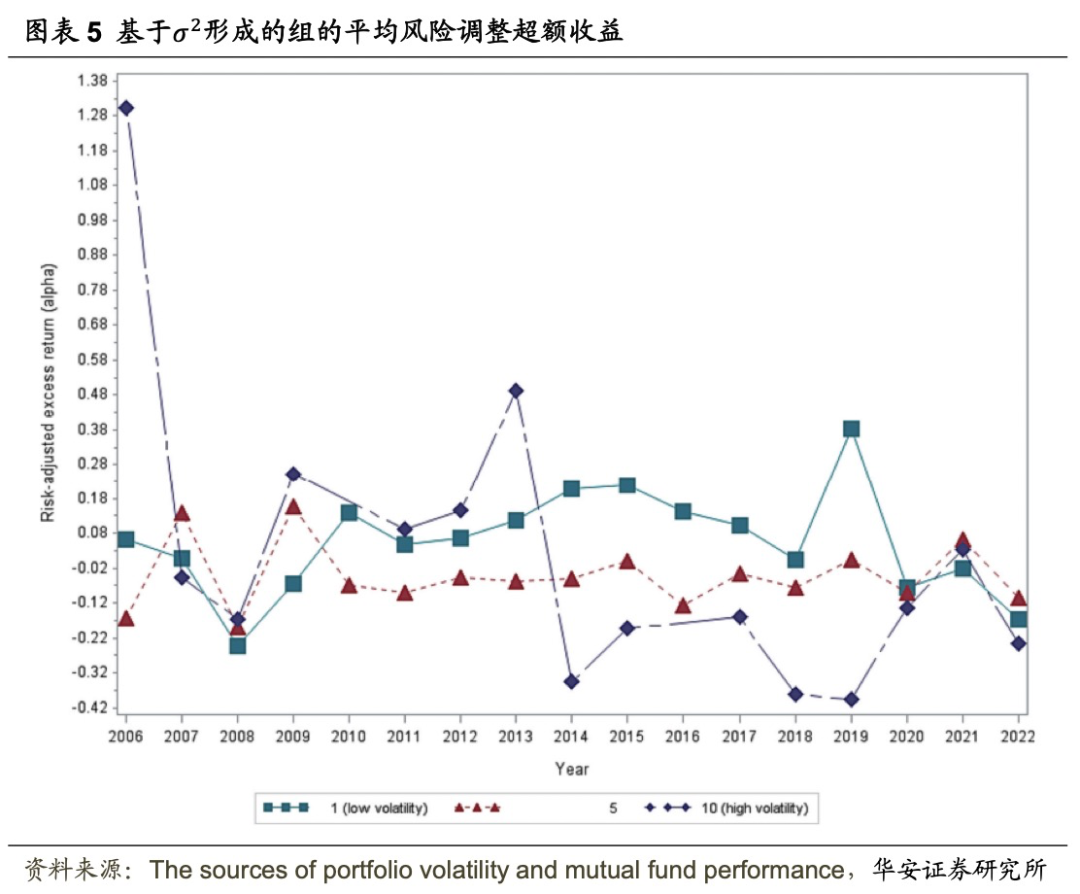
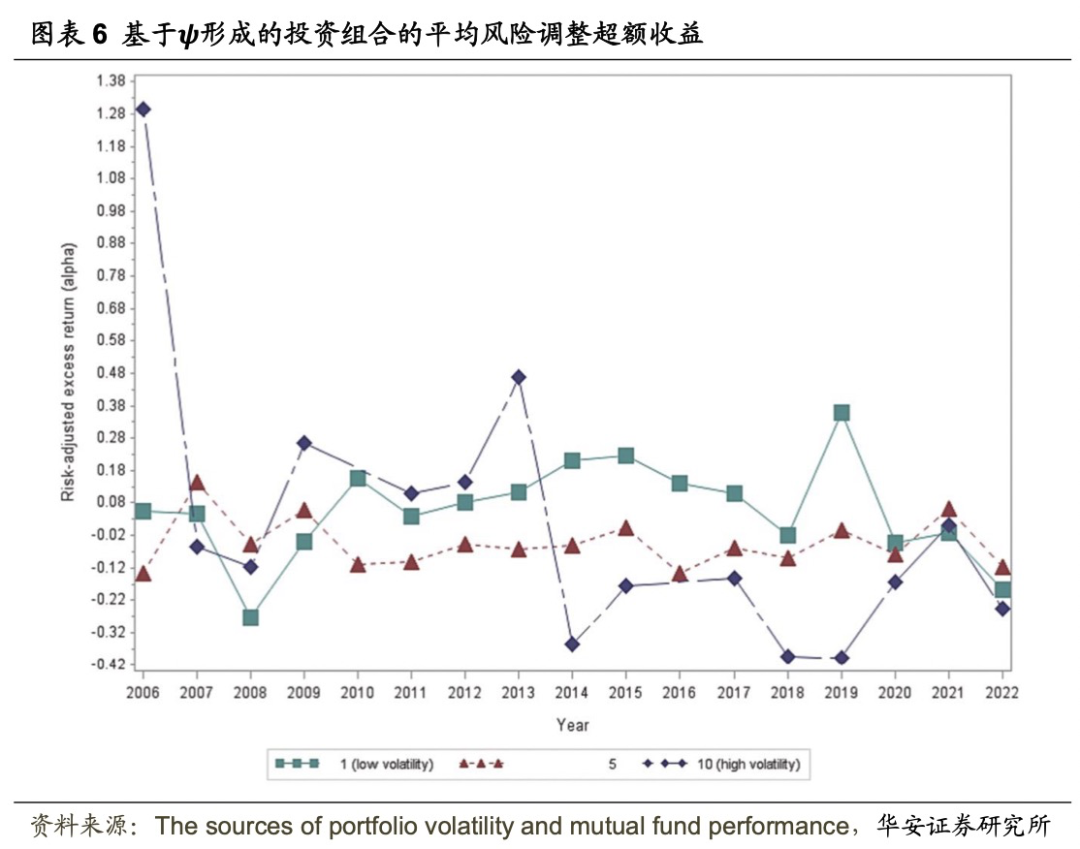
图表6列出了每年根据ψ划分的基金组的alpha值。与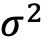 相比,以ψ为基础的组的表现更加稳定。只有在 2008 年和 2009 年,高ψ组的表现才超过低ψ组的表现。这表明,在异常高波动率或危机期间,持股协方差与收益之间的关系会发生逆转。
相比,以ψ为基础的组的表现更加稳定。只有在 2008 年和 2009 年,高ψ组的表现才超过低ψ组的表现。这表明,在异常高波动率或危机期间,持股协方差与收益之间的关系会发生逆转。
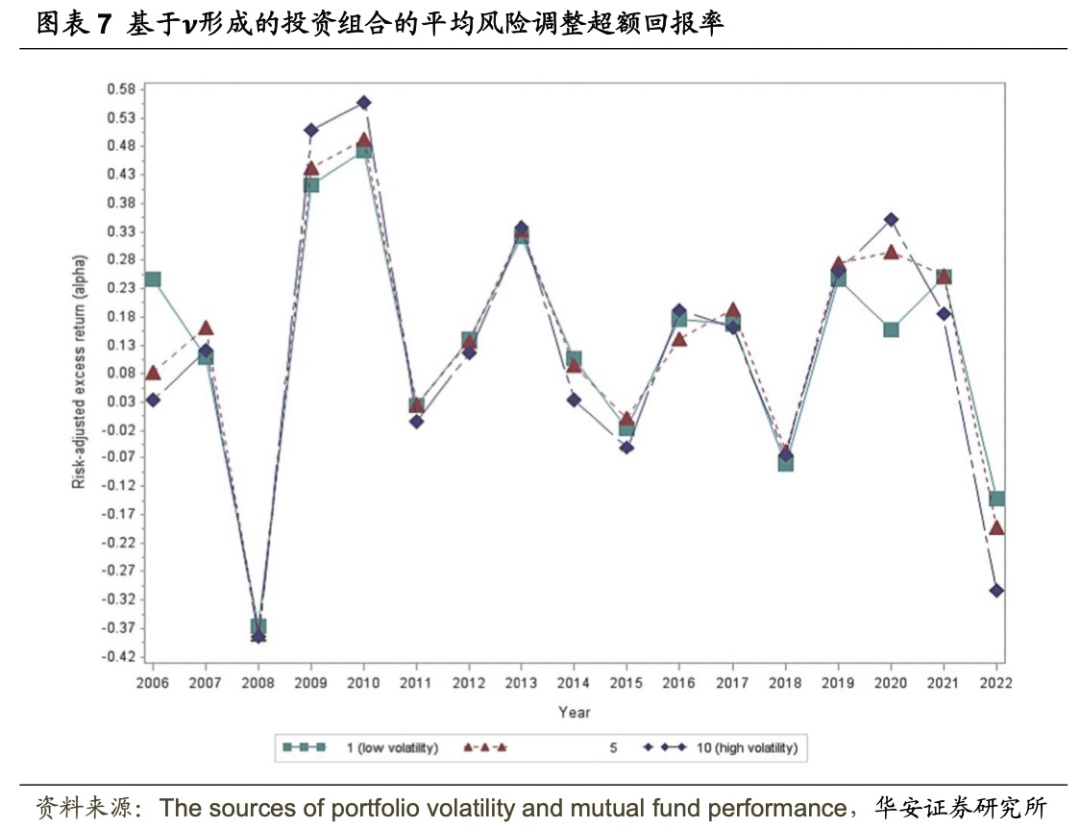
图表7表明,ν所形成的十分组差异随时间的变化相对较小。
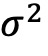 、ψ和ν分组分组的基金的 Fama-French 风险因子敞口。在三个波动率指标中,高波动率组对市场超额收益率、SMB 和 UMD 的因子载荷较大,而低波动率组对HML 因子的载荷更大、更显著。低波动率组的alpha也明显高于高波动率组。
、ψ和ν分组分组的基金的 Fama-French 风险因子敞口。在三个波动率指标中,高波动率组对市场超额收益率、SMB 和 UMD 的因子载荷较大,而低波动率组对HML 因子的载荷更大、更显著。低波动率组的alpha也明显高于高波动率组。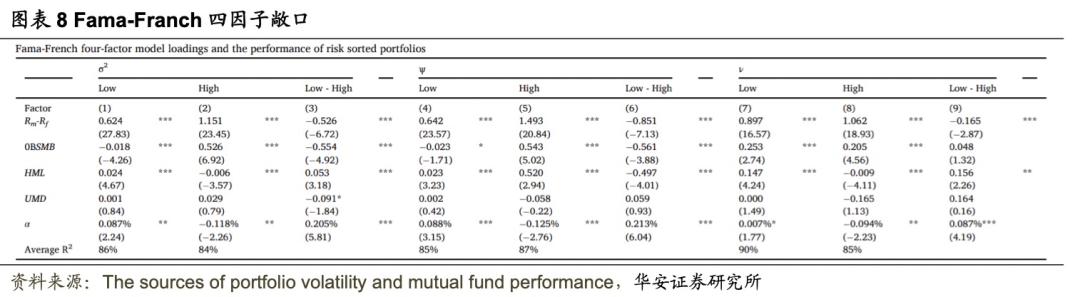
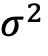 的估计值与ψ的系数估计值的大小和显著性相似。
的估计值与ψ的系数估计值的大小和显著性相似。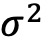 的预测能力完全来自基金持仓收益的ψ部分,尽管这种预测能力的幅度较低。在未列表的结果中,Fama-French 三因子模型也得到了类似的结果。
的预测能力完全来自基金持仓收益的ψ部分,尽管这种预测能力的幅度较低。在未列表的结果中,Fama-French 三因子模型也得到了类似的结果。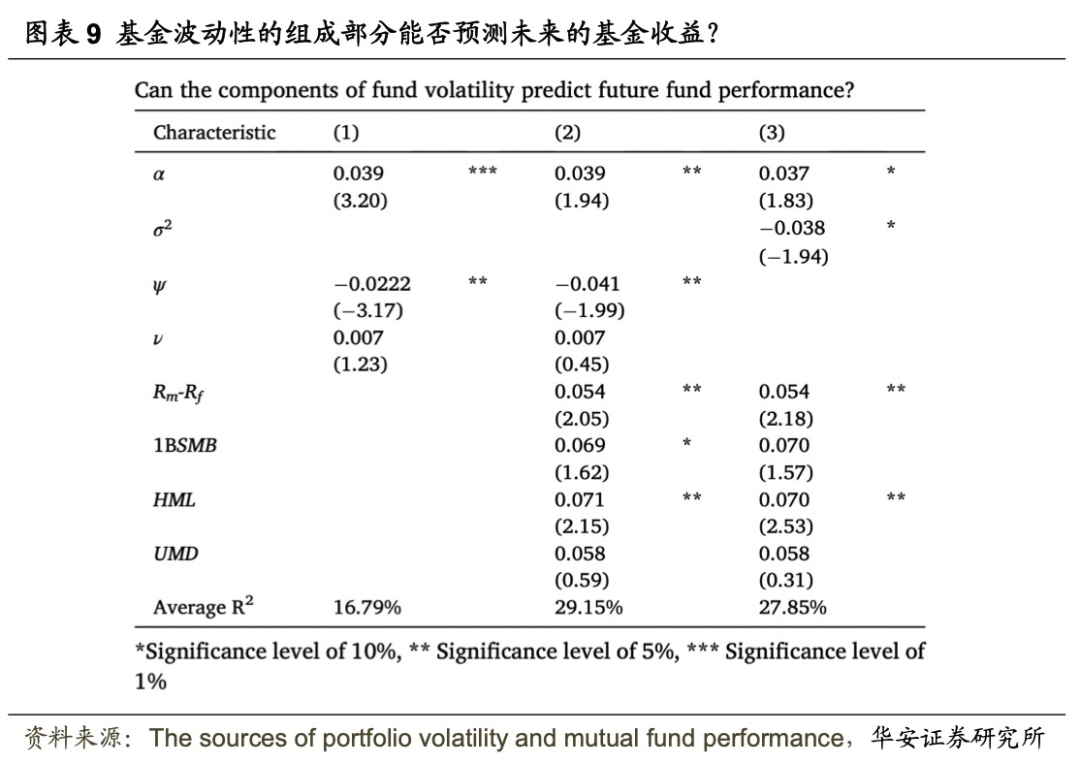
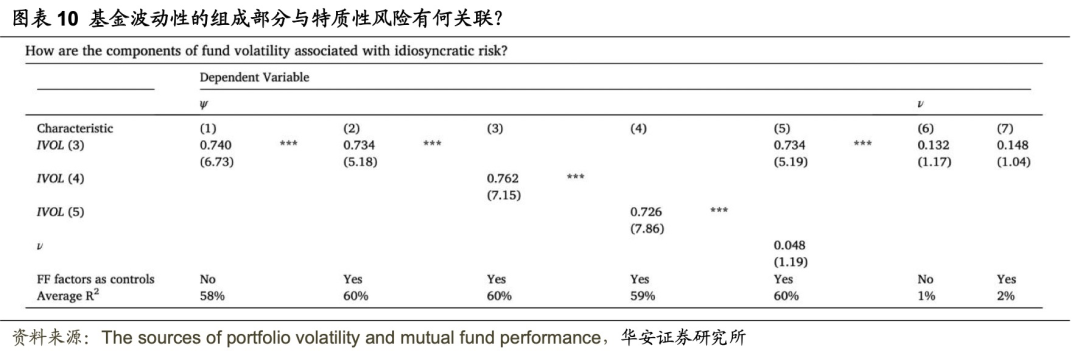
图表10报告了ψ和ν与特质波动率的关系。在(1)至(5)列中,以ψ为因变量估计模型(7)。在(6)和(7)列中,以ν作为因变量估计模型(8)。
模型(7)和(8)采用 Fama 和 MacBeth(1973)的方法进行估计,使用Fama-French的三因子、四因子和五因子模型来估计特质波动率(IVOL)。图表10显示,特质波动率与ψ密切相关,但与ν无关。模型的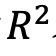 表明特质波动率对ψ的解释能力很强,而对ν的解释能力较弱。
表明特质波动率对ψ的解释能力很强,而对ν的解释能力较弱。
考虑到 Jordan 和 Riley(2015)的研究结果,特异波动在解释ψ方面的重要性就显得很有趣了。Jordan 和 Riley 发现,基金收益与总波动率密切相关,但与特质波动率无关(Jordan & Riley, 2015)。这表明,ψ能捕捉到与特异波动异常(Ang 等人,2006)相关的效应,而这种效应只有在证券水平波动被分解为方差和平均协方差时才会显现出来。
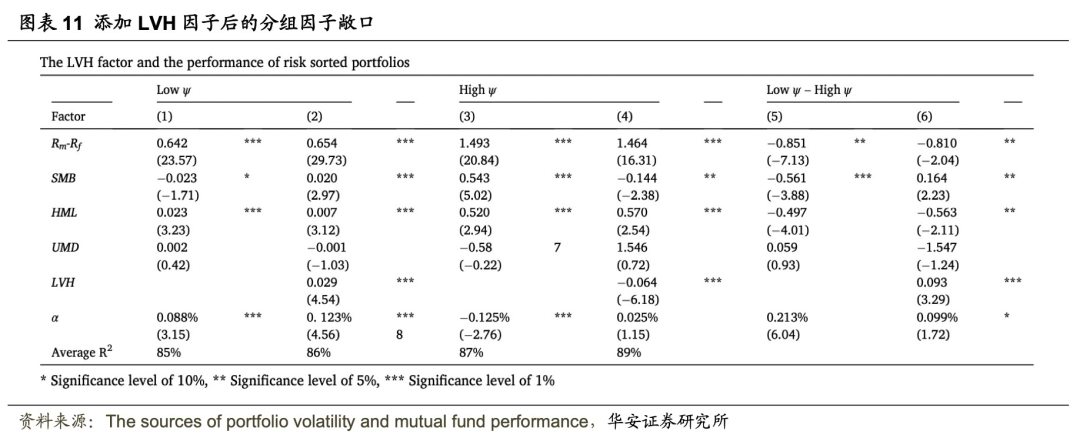
有趣的是,发现 LVH 因子载荷很弱。这表明以基于ψ排序的十分组的回报与 LVH 的关联性很弱。低ψ组的alpha更大且更显著,高ψ组的alpha更小且更显著。这一结果与 Jordan 和 Riley(2015)年的结论有矛盾,他们发现在加入 LVH 因子后,alpha接近于零且变得不显著。
与 Jordan 和 Riley 的结果之间的差异从另一个角度说明了ψ与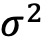 的不同,也说明了这两个指标并不能捕捉到投资组合收益产生过程的相同方面。Jordan 和 Riley(2015)指出,使用 LVH 来解释按波动率排序的基金收益会带来内生性问题。
的不同,也说明了这两个指标并不能捕捉到投资组合收益产生过程的相同方面。Jordan 和 Riley(2015)指出,使用 LVH 来解释按波动率排序的基金收益会带来内生性问题。
接着来看看在考虑贝塔异象时的分解结果如何。图表12面板 A 报告了根据贝塔值和ψ的双重排序形成的十分组的年化收益率。如果协方差仅仅反映了贝塔异象,那么贝塔异象的影响应该只集中在分组的顶部或底部。
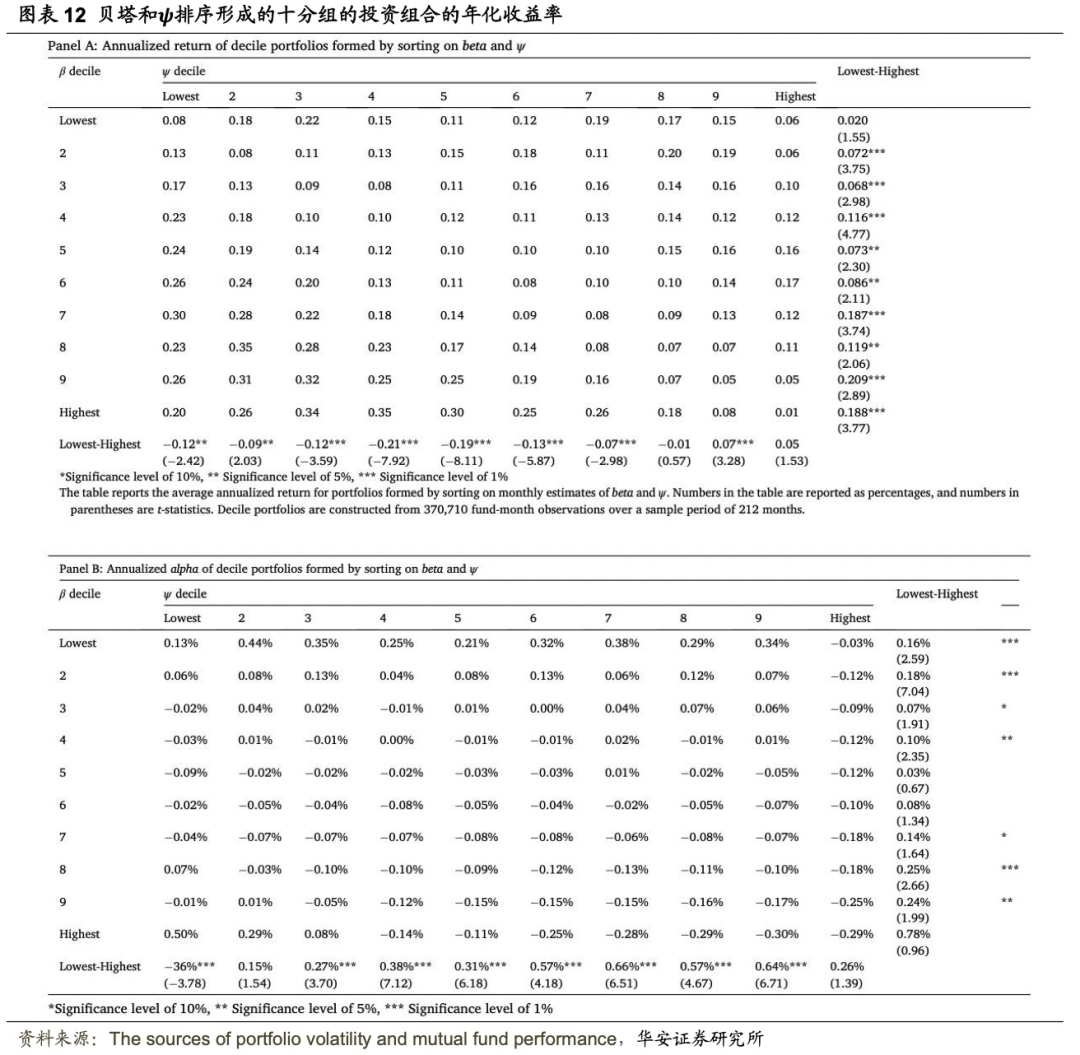
图表12面板 A 的最后一列显示了基于ψ排序的各分组基金在不同贝塔值之间的差异。其中,所有低ψ组减去高ψ组均产生正差异,多数差异显著为正。这表明持仓协方差的影响并不是简单地反映贝塔异常。
图表12面板B报告了按贝塔值和ψ双重排序的年化四因子alpha值的结果,这些风险调整收益率比原始收益率更有意义。最后一列的结果再次表明,在所有贝塔分组中,低ψ组的表现都优于高ψ组。这些结果证实,ψ所反映的持股协方差的影响与贝塔异象不同。从图表12面板 B 的最下面一行可以看出,除了ψ最高的组别外,其他十分组都存在贝塔异象。
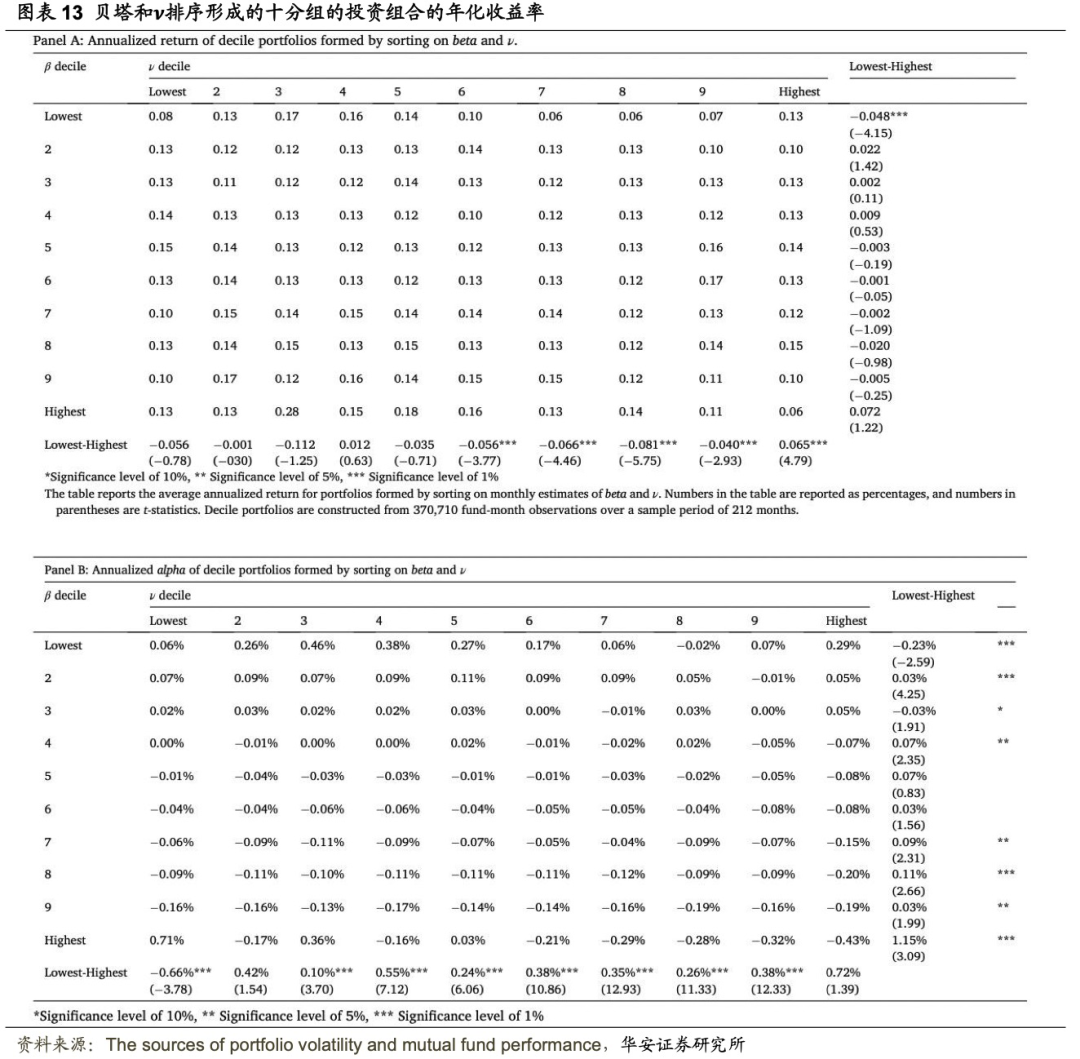
图表13列出了贝塔系数和ν的双分组。在面板A中贝塔异象仅出现在第 2、4 和 10 组中,且观察到一个有趣的模式,即不同贝塔分组的基金持股方差与收益率的关系。在贝塔值最高和最低的组别中,低贝塔值和高贝塔值之间的差异显著。在低贝塔分组中,高贝塔基金的表现明显优于低贝塔基金,而在高贝塔分组中,高贝塔基金的表现明显低于低贝塔基金。基于ν的原始回报差的幅度不大。这表明,任何基金层面的持股方差模式都只集中在那些具有极端(或错误估计)贝塔的基金中。基于ν的波动率异常与极端贝塔密切相关,这一观察结果与直觉相反,因为ν的构建是为了捕捉特定证券的方差,应该与基金层面的极端贝塔值无关。
图表13的面板B显示了基于基金贝塔系数和ν的风险调整回报结果。从面板 B 的最后一列可以看出,除了贝塔系数最低的组别外,其他所有基金都存在基于ν的波动异常,即低ν基金的收益高于高ν基金。在高贝塔组中,低贝塔基金与高贝塔基金之间的差异显著。在贝塔系数最高的基金中,波动异常的幅度最大,平均每年约为 1.77%。对于贝塔系数最低的组别,观察到的结果与波动异常相反:高贝塔系数基金的收益明显高于低贝塔系数基金。图表13面板 B 的最下面一行显示了不同ν分组的贝塔异象检验结果。除了最低组外,贝塔异象一般都是正的、显著的。
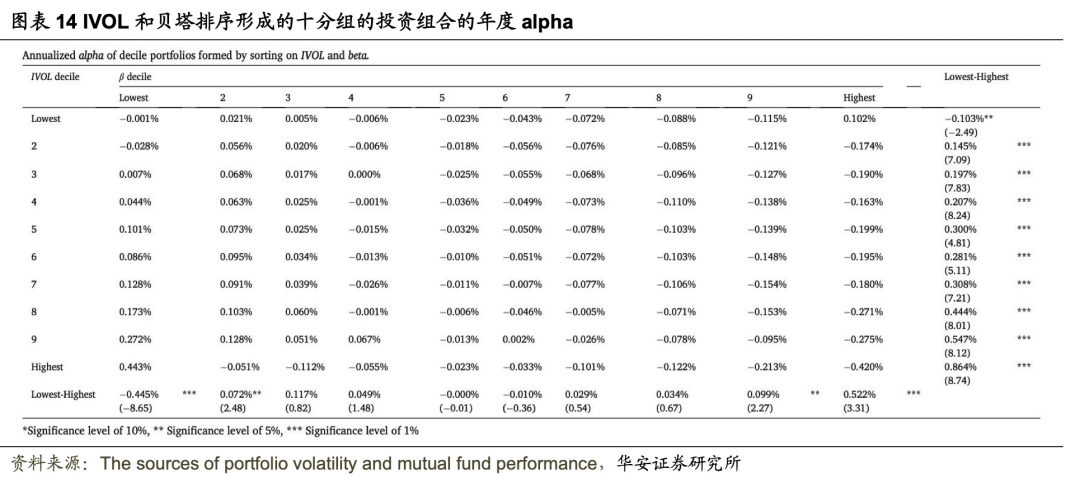
为了研究贝塔系数、特质波动率和持仓波动率如何相互作用,每月对 IVOL 和贝塔值进行双重排序,以观察 IVOL 和贝塔值之间的关联。图表14最后一列显示,除了 IVOL 最低组,所有 IVOL 分组的贝塔都存在强烈且显著的异象,也就是说,多数情况下低贝塔基金的表现优于高贝塔基金,这些结果与 Liu 等人(2018)的报告一致。
在最后一行,观察到 IVOL 异象集中在高贝塔组别中(第7 到 9组)。图表12、图表13、图表14的比较使我们对结果有了更全面的了解。ψ的影响存在于十分组的贝塔中(图表12),但 IVOL 或ν的影响不存在于十分组的贝塔值中(图表12、图表14),IVOL或ν的影响只集中在几个组中。总之,ψ对基金回报的影响比ν对基金回报的影响更普遍。
04
此外,本研究不仅深化了对波动率异常的认识,还为理解投资组合内部证券协方差在资产定价中的作用提供了新的视角,对于投资组合管理和风险评估具有重要的实践意义。
文献来源:
风险提示
文献结论基于历史数据与海外文献进行总结;不构成任何投资建议。
——“学海拾珠”系列之一百六十六》(发布时间:20231115),具体分析内容请详见报告。若因对报告的摘编等产生歧义,应以报告发布当日的完整内容为准。分析师:严佳炜 || 执业证书号:S0010520070001,分析师:钱静闲 || 执业证书号:S0010522090002。
50.《投资者评价基金时会考虑哪些因素?》
142.《多只新股上市首日涨幅超100%,情绪维持”高温“》
138.《新股市场受资金追捧,打新收益陡升》
122.《科创板新股首日涨幅回暖,首批注册制主板新股迎来上市》
49.《多只新股破发,打新收益曲线调整》
43.《打新账户数量企稳,预计全年2亿A类收益率11.86%》


有态度的金融工程&FOF研究

本篇文章来源于微信公众号: 金工严选