收缩调整夏普比率：一种更优的选择共同基金的方法

admin2年前 (2023-02-11)研报1055

导读

作为西学东渐--海外文献推荐系列报告第一百五十篇，本文推荐了Moshe Levy和Richard Roll于2022年发表的论文《The Shrinkage Adjusted Sharpe Ratio: An Improved Method for Mutual Fund Selection》。
历史夏普比是投资者选择基金最常用的指标之一，投资者希望历史表现优异的基金未来能够延续其优势表现，但简单的历史夏普比率在预测基金未来表现上的效果不够理想，因此本文尝试对夏普比进行改良。
本文改良的原理如下：历史基金收益相对未来基金收益是有噪声的估计项，但基金费用对未来基金收益却是已知的（无噪声的）扣减项，因此在估计未来基金收益时应当适当放大基金费用的权重。为了实现这一点，本文引入Bayes-James-Stein估计量中的收缩因子构造了收缩调整的夏普比率(Shrinkage Adjusted Sharpe ratio 简称(SAS))，通过收缩因子在SAS指标中适当增加费用的权重，减少历史收益的权重。
实证结果表明，SAS指标对未来基金业绩的预测能力显著优于简单夏普比率，并且这个指标对于不同的基金类型、时间区间以及估计窗口的预测结果均比较稳健。

风险提示：文献中的结果均由相应作者通过历史数据统计、建模和测算完成，在政策、市场环境发生变化时模型存在失效的风险。

1、引言

委托资产管理在金融市场上扮演着重要的角色。上个世纪五十年代初期，这项业务仅占美国所有者权益市场的5%，但近年来已上升至50%左右(Gârleanu 和 Pedersen，2021)。2020年，美国共同基金管理规模已达23.9万亿美元，约有47.4%的家庭持有基金。调查显示，大约有50%的美国家庭不参与股票市场(Bogan 2008)，这意味着大多数人通过持有共同基金而持有股票。因此，如何选择优质基金是大多数投资者面临的核心问题。

众所周知，无论使用阿尔法还是夏普比率，基金的历史收益数据对其未来收益的预测效果均不够理想。阿尔法是衡量基金经理相对于系统性风险敞口产生超额收益能力的指标，但对于持有单一基金的投资者来说，需要考虑基金的总风险，因此夏普比率更适合作为衡量基金经理业绩的标准。图1中的A组是美国股票基金的样本内和样本外夏普比率之间的关系(具体数据和实证方法见后文详述)，展示了可观察到的样本内(过去)夏普比率对不可观察到的样本外(未来)的夏普比率的预测能力。该图显示，样本内和样本外的夏普比率之间的关系非常弱，意味着预测能力较差。由于晨星评级与样本内夏普比率密切相关(Sharpe 1998)，所以也不能很好地预测未来的业绩。历史数据对预测未来的业绩作用有限，而数以百万计的家庭却据此进行了数万亿美元的投资,本文的目标就是探索如何能改善这一问题。

考虑两个基金：基金A的年平均总收益率为11%，管理费为1%。基金B的年平均总收益率为12%，收取2%的费用。简单起见，假设这两只基金波动率相同，那么投资者应该选择哪个基金呢？乍一看，这两只基金似乎是无差别的，因为它们的净收益均为10%。但是，平均总收益率是有噪声的估计，而费用是已知的，因此费用的权重应该大于收益的权重。在极端的情况下，即当收益率数据不包括任何关于未来的有用信息时，可以忽略收益率，而只根据费用对基金进行排名。在一般情况下，历史收益率是关于未来收益有噪声的信号，但问题是相较于费用，我们应该给这个信号多少权重呢？这就是本文讨论的主要问题。

我们提出了一个更普适的夏普比率，主要思路是：在Bayes-James-Stein的概念中，“收缩”应该用于样本内总收益率，而费用是确定的，因此不应该调整。由此设计出了一个指标：收缩调整夏普比率，即SAS。标准夏普比率与Levy和Roll(2018)提出的收缩夏普比率是SAS的特例。

我们发现，SAS对基金未来业绩的预测比夏普比率好得多。图1中的B组显示：样本内SAS对样本外夏普比率的解释力更强(R方为0.934)。投资者自然会把注意力集中在历史业绩更高的基金上，所以这些基金的未来业绩表现是非常重要的。在1991-2021年期间，如果采用平均加权法投资于样本内夏普比率最高的前10只基金，可以得到样本外的月度夏普比率为0.109，远远低于同期S&P500指数的月度夏普比率，即0.148。相比之下，投资于样本内SAS最高的前10只基金，产生的样本外夏普比率为0.169(详见第三节)。而且，根据SAS指标选出来的基金不仅未来业绩表现得更好，它们甚至在年度风险调整后收益上超出市场约1.1%。

2、收缩调整夏普比率（SAS）

从投资者选择共同基金的角度来看，基金的业绩表现应该用扣除费用后的收益来衡量。SAS指标构建的思路是：在Bayes-James-Stein的概念上对基金的样本总平均收益进行收缩，但基金费用通常是已知且确定的，因此费用不应被收缩。在估计基金的预期净收益时，应该首先对平均总收益进行收缩，然后再减去费用，而不是直接对净收益进行收缩。

3、数据和结果

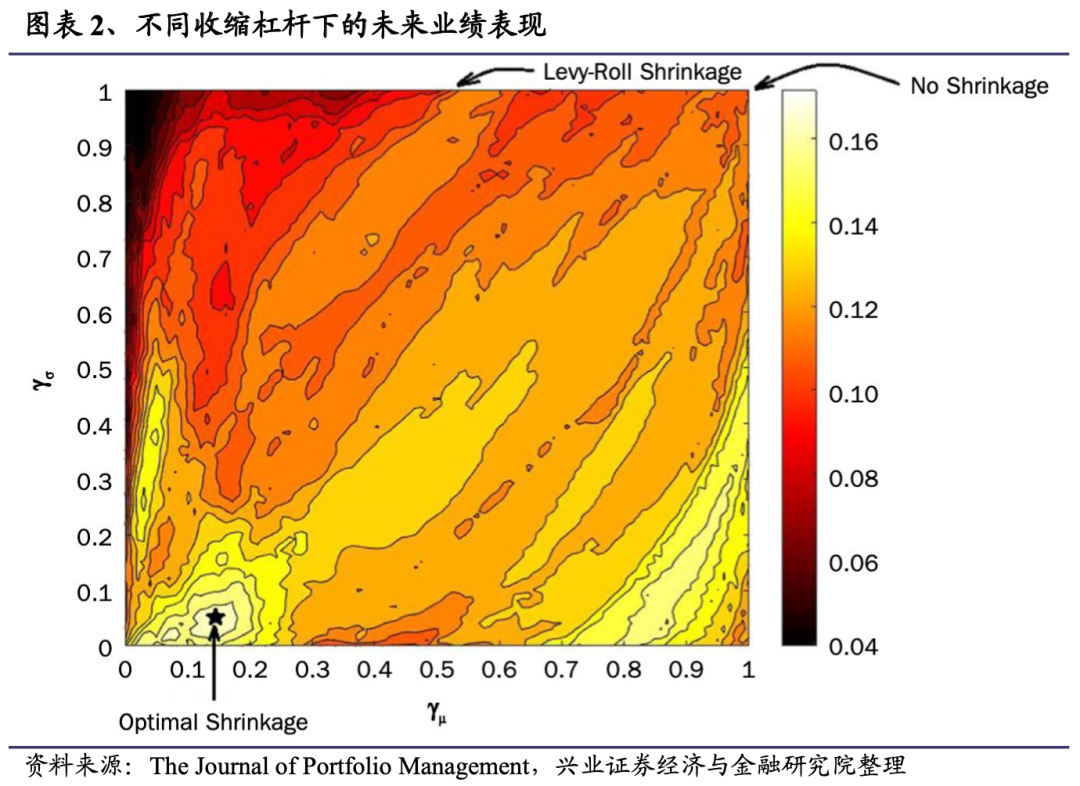
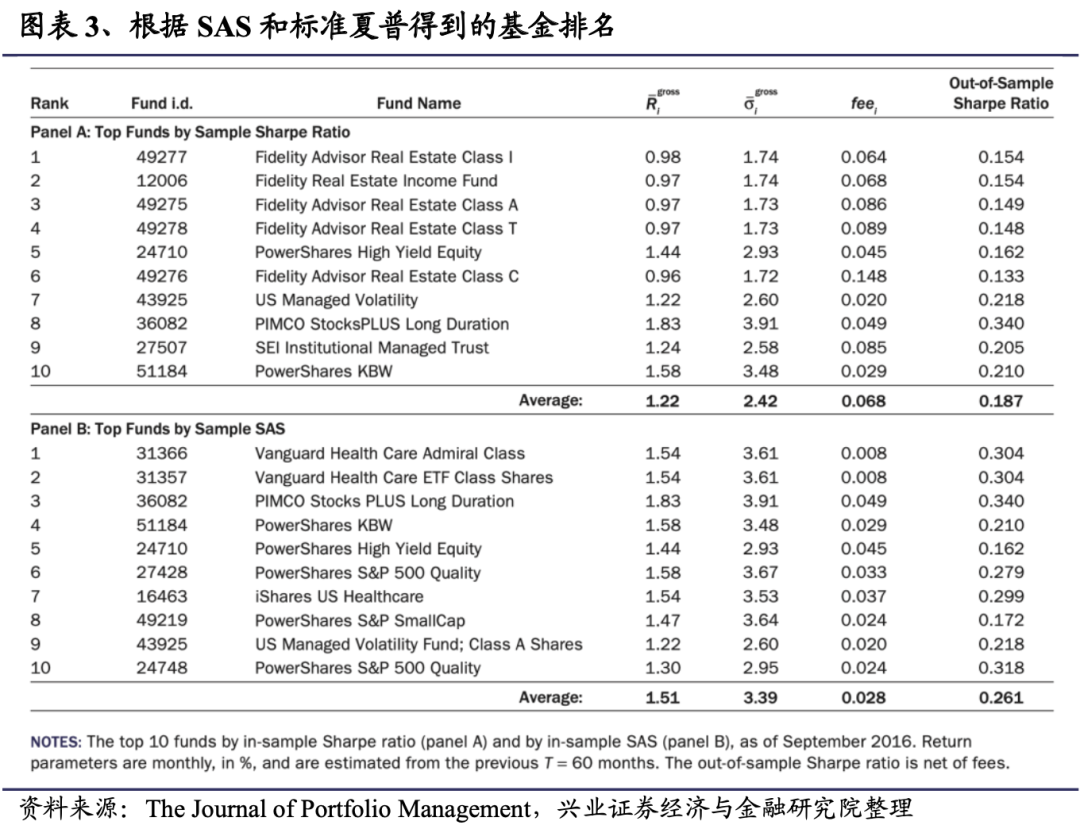
我们的数据来自CRSP无幸存者偏差的共同基金数据库。由于1991年12月之前的月度费用数据大多不可用，因此，我们的数据样本期间为1991年12月至2021年9月(共358个月)。月度无风险利率来自CRSP无风险时间序列。

我们主要研究美国的股票基金(CRSP中风格代码以“ED”开头的所有基金)。在下一节中，我们还单独研究了外国股票基金(CRSP风格代码以“EF”开头的所有基金)，以及公司和市政债券基金(CRSP风格代码以“IC”和“IU”开头的所有基金)。

我们采用两种方法来评估业绩指标。第一种方法是只选出历史数据排名最高的部分基金预测未来业绩。从投资者的角度来看，这样选出来的基金是最有吸引力的。第二种方法是根据所有基金的样本内排名与样本外业绩之间的关系来评估业绩，如图1。这种方法提供了一个更广泛的视角：采用了所有基金数据而不仅仅是排名靠前的基金，具有的统计优势。

在图中用星星表示。由这个组合得到的夏普比率为0.169。这不仅比无收缩和Levy-Roll(2018)方法计算的夏普比率高得多，甚至高于同期市场组合的夏普比率，即0.148。相应地，年度风险调整超额收益约为1.1%，这意味我们可以通过SAS来识别一些超越市场业绩表现的优质基金。

一个关键问题是对于不同的资产类别、样本期间和估计窗口，(7)式中的最优参数值是否稳健，我们将在下一节讨论这个问题。我们发现使用(7)中的参数值确实能普遍对基金的未来业绩表现进行良好的预测,不仅是在第一种方法中如此，而且在考虑所有基金业绩的第二种方法中也是如此：图表1的B组采用了同样的参数值，描述了所有基金的样本内SAS指标和未来夏普比率之间的关系。图1根据样本内业绩将基金分为十等份，但如果将基金按业绩排名分为100个百分位数，也会得到非常相似的结果(见附录B)。

为了更好地研究使用SAS和标准夏普比率得到的基金排名差异，让我们看看由这两个指标确定的前10名基金。图表3提供了截至到2016年9月估计窗口为60个月的基金样本内参数：平均总收益、标准差和费用，以及相应的扣除费用后的样本外夏普比率。样本内数据是投资者在2016年9月时能观察到的数据，样本外的夏普比率是“未来”(即2016年10月至2021年9月期间)每只基金的夏普比率，这些显然是投资者在2016年9月无法观察到的(因为是未来的夏普比率)。这两组基金之间最明显的区别是费用：根据普通夏普比率选择的基金平均每月费用为0.068%，而根据SAS选出的基金的费用仅为0.028%，这是因为SAS指标中的费用权重过高。由于赋予样本方差的权重非常小，根据SAS指标选出的基金波动率比根据夏普比率选出的基金高。由于较高波动率的基金往往也有较高的平均收益，因此根据SAS排名选出的基金也会有较高的收益，其夏普比率高出39.6%。此外，如果按照样本外的夏普比率对基金进行排名，每个SAS基金的样本外夏普比率都高于其对应的夏普基金(类似于一种分布对另一种分布的一阶随机占优，见Hadar和Russell 1969，以及Hanoch和Levy 1969)。

4、关于稳健性的讨论

我们通过几种方式检验了SAS预测表现与(7)式中收缩参数的稳健性。首先，我们研究了不同的基金类别，分别考察了外国股票基金和市政债券基金。其次，我们对样本期间进行拆分，考察美国股票基金分别在1991-2006年和2006-2021年这两个子时期的表现。最后，我们研究了估计窗口长度T的稳健性。

4.1

资产类别

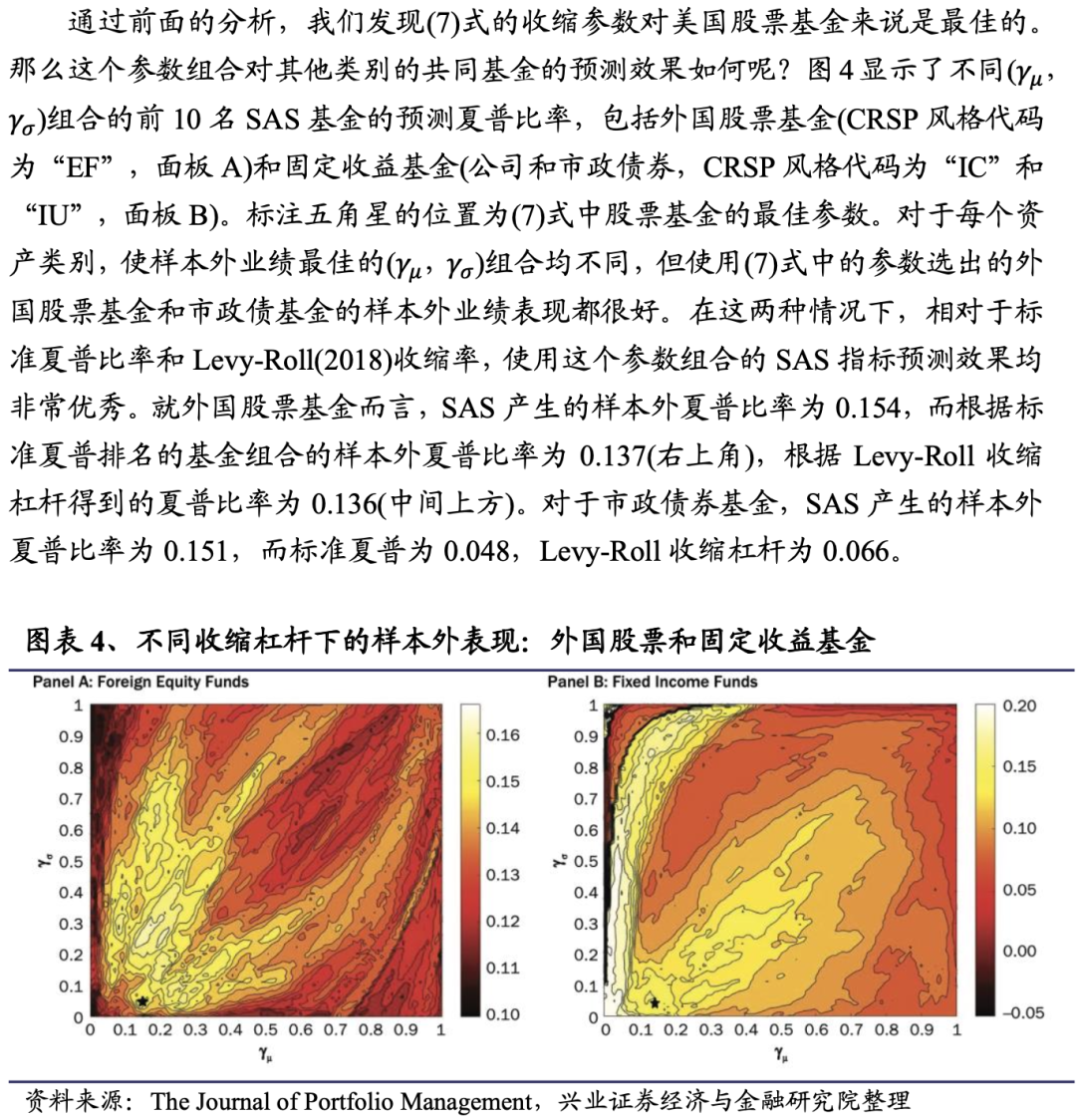
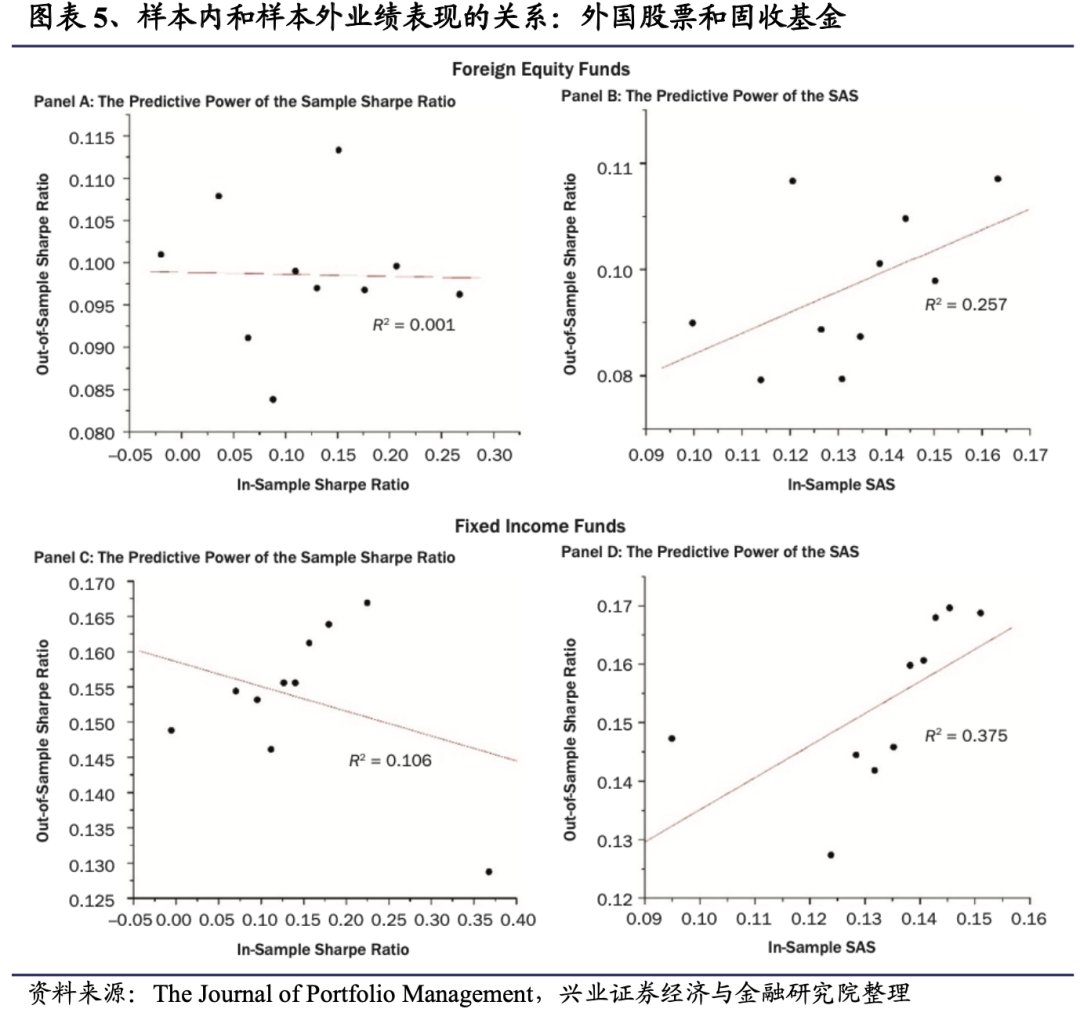
4.2

不同的样本区间

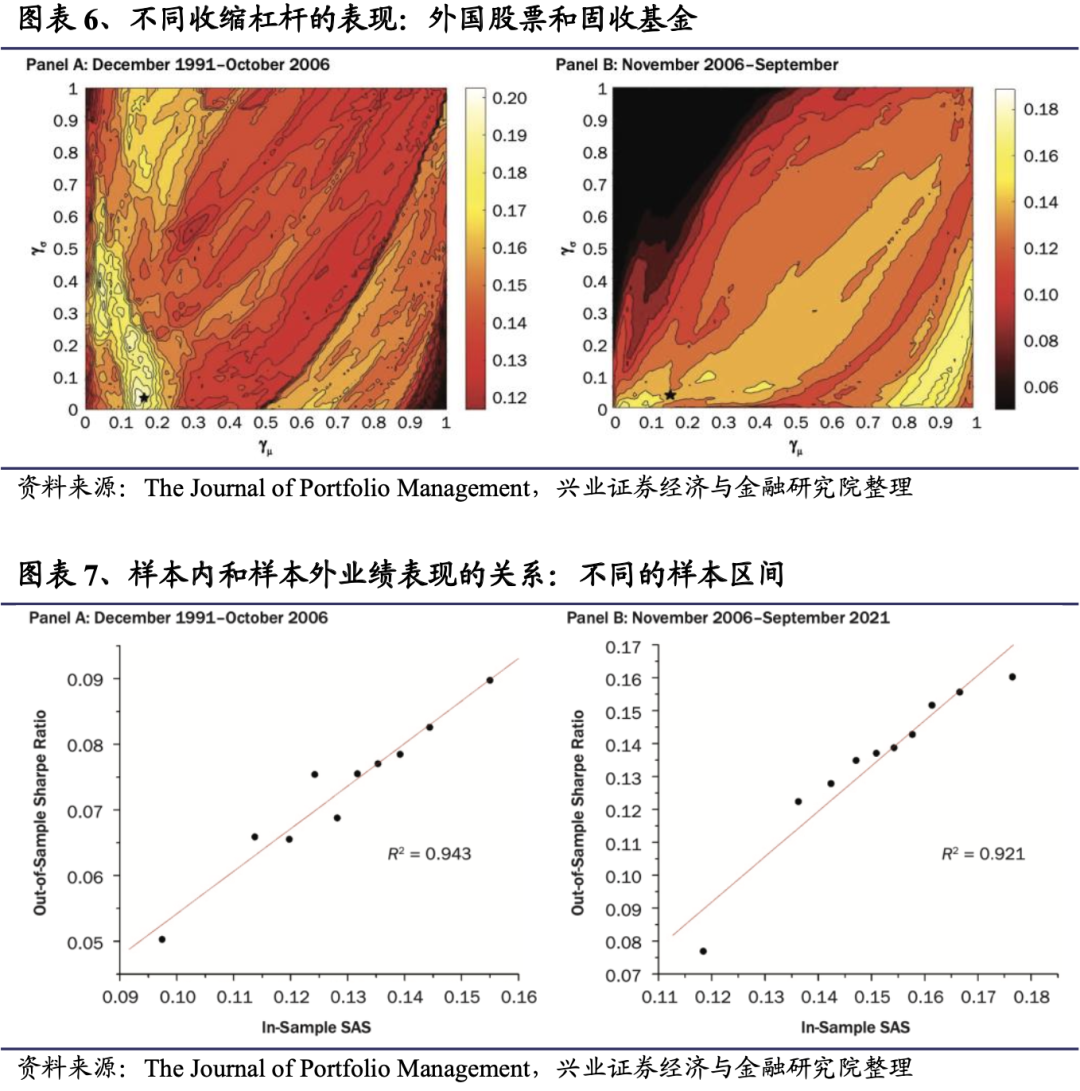
为了检验结果在不同时期是否稳健，我们将样本期分为两个子时期，并对每个子时期单独进行分析。第一个子时期是1991年12月至2006年10月，第二个子时期是2006年11月至2021年9月。图6和图7报告了结果：图6为排名前10的美国国内股票基金，图7为所有的美国股票基金。在这两个子时期，(7)式中的收缩参数(用星号表示)表现良好，超过标准夏普比率(无收缩杠杆)和Levy-Roll（2018）的收缩杠杆的表现。在第一个子时期，前10名SAS基金产生的样本外夏普比率为0.198，而前10名夏普基金的样本外夏普比率为0.137，Levy-Roll收缩杠杆挑选出的基金夏普比率为0.132。在第二个子时期，前10名SAS基金产生的样本外夏普比率为0.142，而夏普基金的比率为0.127，Levy-Roll收缩杠杆的比率为0.115。

4.3

更短的估计窗口

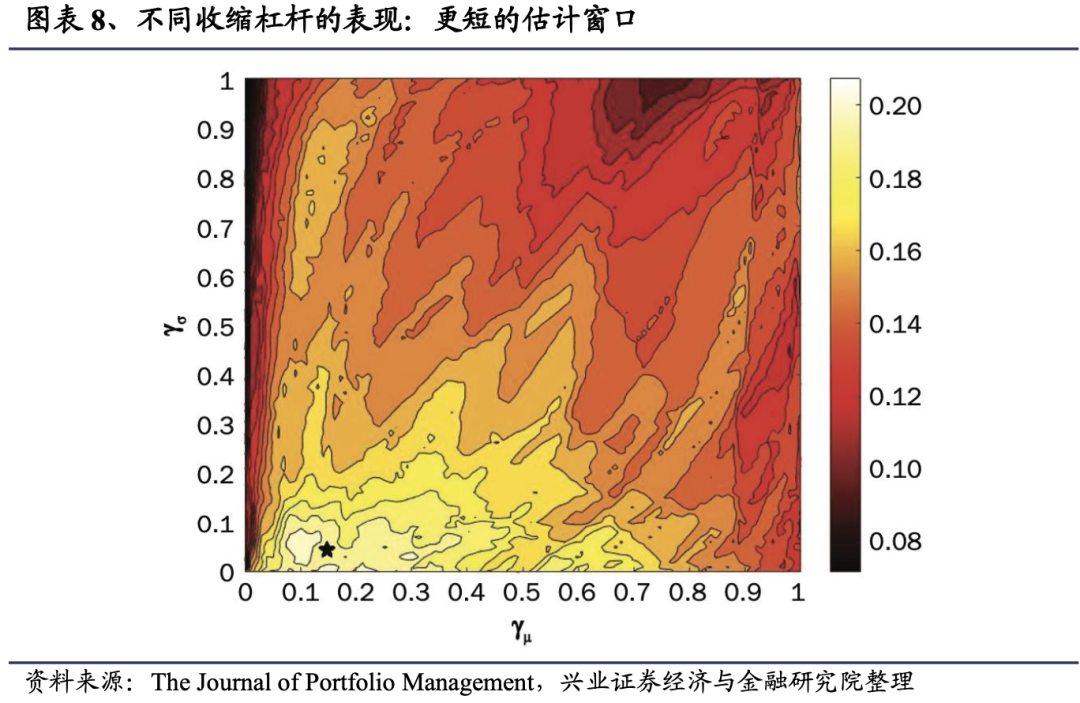
5、总结

金融领域中收缩杠杆的应用很广泛，比如，投资组合优化中收益参数的收缩(Jorion 1985，1986，DeMiguel，Martin-Utrera和Nogales 2013，Ledoit和Wolf 2004，2017，2020，以及Kircher和Rosch 2021)，资本成本估计中贝塔的收缩(Jorin 1991，Genton和Ronchetti 2008，Levi和Welch 2017)，收缩阿尔法(Jones和Shanken 2005，Harvey和Liu 2018)以及模型不确定情况下的收缩(Wang 2005，Garlappi，Uppal和Wang 2007)。在本文的研究中，我们将收缩的概念应用于共同基金的选择中。本文的核心观点是样本总收益参数需要收缩，而不收缩已知费用，在此基础上构造了收缩调整夏普比率(SAS)。

如果收益的分布是时间序列平稳的，那么可以得到最佳的收缩杠杆。然而实际上，收益分布可能会以一种未知的方式随时间变化，因此，我们难以计算最佳收缩杠杆。在本文的最后，我们进行了稳健性分析，发现最佳收缩杠杆对共同基金的资产类别、不同的样本期间和不同的用于估计收益参数的窗口长度来说均相当稳健。无论是对样本内中排名靠前的基金，还是对所有基金进行样本外业绩评估时，情况都是如此。我们发现最佳收缩杠杆的参数组合意味着基金费用比平均收益的权重大5倍左右。这意味着，基金收益率相差5个基点的情况下，费用差异为1个基点才是合理的。

排名靠前的SAS基金的样本外业绩不仅优于按标准样本夏普比率筛选或按Levy和Roll(2018)衡量的排名靠前的基金，还大大优于市场组合的业绩，在年度风险调整后收益上高出1.1%。因此，SAS指标让我们能够事先识别这些能够持续跑赢市场的基金。

6、附录

6.1

附录A：

共同基金的选择：夏普v.s.阿尔法

作为衡量基金经理业绩的方法，阿尔法一直很受欢迎，它提供了控制系统风险因素后超额回报的衡量标准。但对于选择单一共同基金的投资者来说，这个衡量标准不再适用，因为投资者关心的是基金的方差，包括其非系统性风险部分。换句话说，基金指数与投资者持有基金的预期效用并不十分相关。图9的B组说明了这一点。

在收益正态分布和存在无风险资产的假设下，风险规避的投资者预期效用最大化与夏普比率的最大化是完全一致的(Sharpe 1966，1994，Hanoch和Levy 1969)。这一结果后来被扩展到所有具有非递减偏好的投资者(Levy和Levy 2004，Levy、De Giorgi和Hens 2012)，包括具有前景理论偏好和具有不同期望水平的投资者。Levy和Markowitz(1979)以及Kroll、Levy和Markowitz(1984年)表明，即使回报分布不完全是正态分布的，MV优化是预期效用最大化很好的近似值。

图9显示了阿尔法、夏普与效用函数为对数的投资者的预期效用之间的关系。数据为所有美国股票共同基金2016年10月至2021年9月这60个月期间的60个月度收益。对于每个共同基金，我们用四因子模型计算阿尔法，夏普比率，以及在最佳资产配置下(即在基金和无风险资产之间的最佳分散化下)产生的预期效用。图中A显示，夏普比率和预期效用之间几乎是单调的关系，Spearman等级相关度为0.987。因此，即使收益不是正态分布的，夏普比率也与投资者的预期效用非常接近。B图显示了基金的Fama-French-Carhart 四因素阿尔法与预期效用之间的关系。在这种情况下，Spearman相关度只有0.391。因此，虽然夏普比率与预期效用最大化几乎完全一致，但选择具有最高阿尔法的基金意味着低于平均水平的预期效用。对于不同的效用函数，以及Fama-French(2015)的五因素模型，也能得到类似的结果。

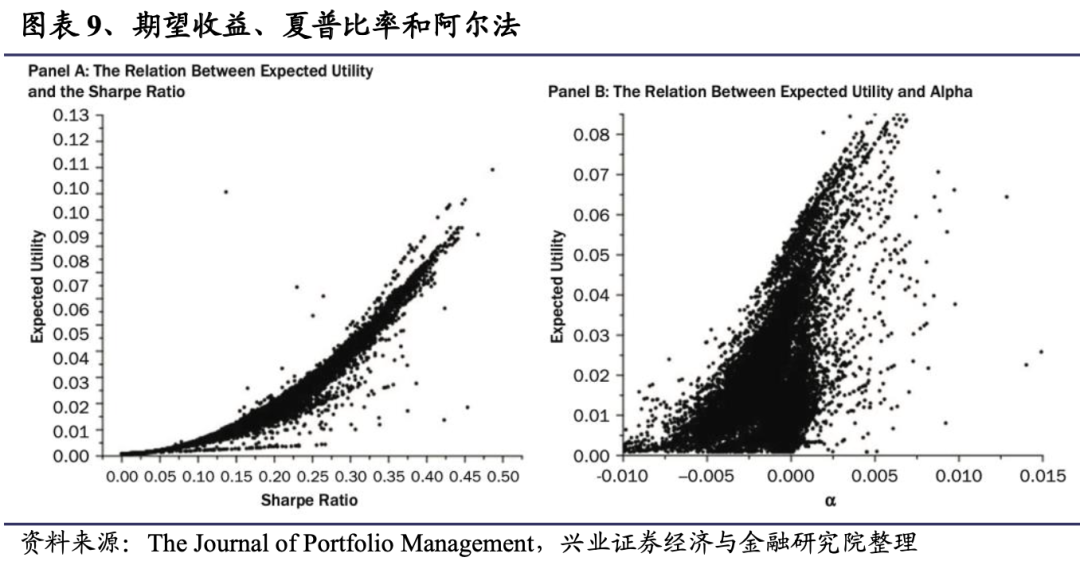
6.2

附录B：百分位业绩表现

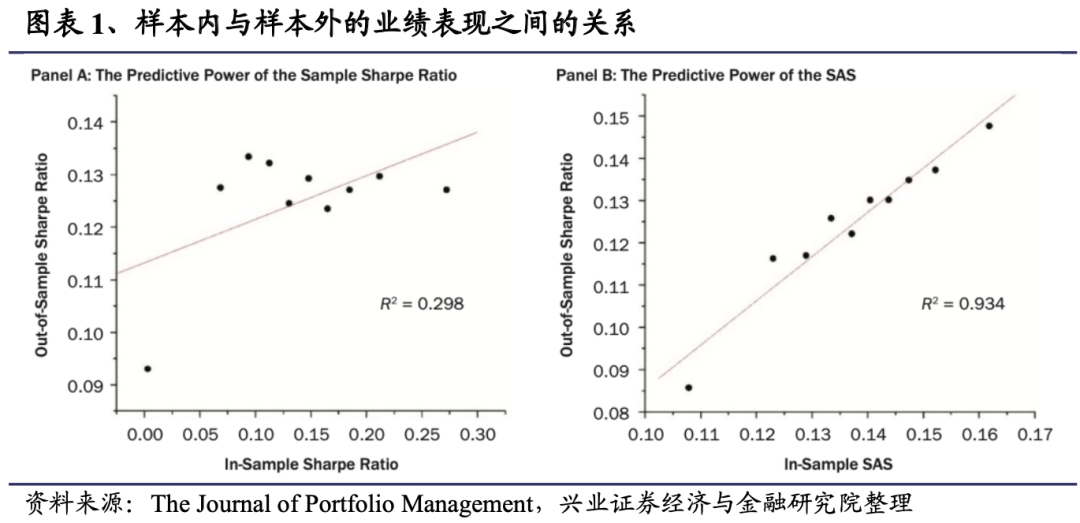
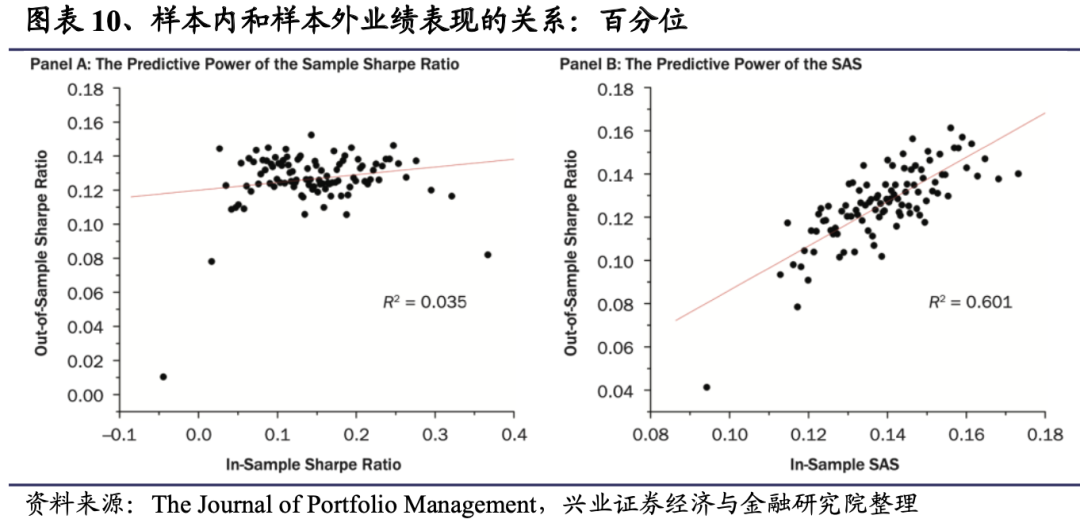
下图为样本内业绩与样本外夏普比率之间的关系。采用所有美国股票基金1991年12月至2021年9月(数据和实证方法的详细描述见第3节)的数据。根据基金的样本内业绩进行排名，并将其分为100个百分位数。对于每个百分位数，计算样本内平均业绩和样本外平均夏普比率(扣除费用)。A组以标准夏普比率(扣除费用)作为样本内业绩衡量标准。B组以SAS作为业绩衡量标准。

参考文献

[1] Barras, L., O. Scaillet, and R. Wermers. 2010. “False Discoveries in Mutual Fund Performance: Measuring Luck in Estimated Alphas.” The Journal of Finance 65 (1): 179–216.

[2] Bayes, T., and P. Richard. 1763. “An Essay Towards Solving A Problem in the Doctrine of Chance.” Philosophical Transactions of the Royal Society of London 53: 370–418.

[3] Berk, J. B., and J. H. Van Binsbergen. 2015. “Measuring Skill in the Mutual Fund Industry.” Journal of Financial Economics 118 (1): 1–20.

[4] Blake, D., T. Caulfield C. Ioannidis, and I. Tonks. 2017. “New Evidence on Mutual Fund Performance: A Comparison of Alternative Bootstrap Methods.” Journal of Financial and Quantitative Analysis Vol (Issue))?: 1–21.

[5] Bogan, V. 2008. “Stock Market Participation and the Internet.” Journal of Financial and Quantitative Analysis 43 (1): 191–211.

[6] Bollen, N.P., and J. A. Busse. 2001. “On the Timing Ability of Mutual Fund Managers.” The Journal of Finance 56 (3): 1075–1094.

[7] Busse, J. A., T. Chordia, L. Jiang, and Y. Tang. 2021. “Transaction Costs, Portfolio Characteristics, and Mutual Fund Performance.” Management Science 67 (2): 1227–1248.

[8] Carhart, M. M. 1997. “On Persistence in Mutual Fund Performance.” The Journal of Finance 52 (1): 57–82.

[9] Chevalier, J., and G. Ellison. 1999. “Are Some Mutual Fund Managers Better Than Others? Cross-Sectional Patterns in Behavior and Performance.” The Journal of Finance 54 (3): 875–899.

[10] Cremers, K. M., J. A. Fulkerson, and T. B. Riley. 2018. “Benchmark Discrepancies and Mutual Fund Performance Evaluation.” Journal of Financial and Quantitative Analysis 1–52.

[11] Cremers, K. M., and A. Petajisto. 2009. “How Active is Your Fund Manager? A New Measure that Predicts Performance.” The Review of Financial Studies 22 (9): 3329–3365.

[12] Daniel, K., M. Grinblatt, S. Titman, and R. Wermers. 1997. “Measuring Mutual Fund Performance with Characteristic-Based Benchmarks.” The Journal of Finance 52 (3): 1035–1058.

[13] DeMiguel, V., A. Martin-Utrera, and F. J. Nogales. 2013. “Size Matters: Optimal Calibration of Shrinkage Estimators for Portfolio Selection.” Journal of Banking and Finance 37 (8): 3018–3034. Fama, E. F. The Journal of Finance 65 (5): 1915–1947.

[14] Fama, E. F., and K. R. French. 2015. “A Five-Factor Asset Pricing Model.” Journal of Financial Economics 116 (1): 1–22.

[15] Garlappi, L., R. Uppal, and T. Wang. 2007. “Portfolio Selection with Parameter and Model Uncer- tainty: A Multi-Prior Approach.” The Review of Financial Studies 20 (1): 41–81.

[16] Gârleanu, N., and L. H. Pedersen. 2021. “Active and Passive Investing: Understanding Samuelson’s Dictum.” Review of Asset Pricing Studies, forthcoming.

[17] Genton, M.G., and E. Ronchetti. Robust Prediction of Beta. In Computational Methods in Financial Engineering Springer, Berlin, Heidelberg. 2008.

[18] Guercio, D. D., and J. Reuter. 2014. “Mutual Fund Performance and the Incentive to Generate Alpha.” The Journal of Finance 69 (4): 1673–1704.

[19] Hadar, J., and W. R. Russell. 1969. “Rules for Ordering Uncertain Prospects.” The American Economic Review 59 (1): 25–34.

[20] Hanoch, G., and H. Levy. 1969. “The Efficiency Analysis of Choices Involving Risk.” The Review of Economic Studies 36 (3): 335–346.

[21] Harvey, C. R., and Y. Liu. 2018. “Detecting Repeatable Performance.” The Review of Financial Studies 31 (7): 2499–2552.

[22] Harvey, C. R., and Y. Liu. 2020. “Luck versus Skill in the Cross-Section of Mutual Fund Returns: Reexamining the Evidence.” Available at SSRN 3623537.

[23] James, W., and C. Stein. Estimation with Quadratic Loss. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Contributions to the Theory of Statistics. 1961.

[24] Jiang, H., and M. Verardo. 2018. “Does Herding Behavior Reveal Skill? An Analysis of Mutual Fund Performance.” The Journal of Finance 73 (5): 2229–2269.

[25] Jones, C. S., and J. Shanken. 2005. “Mutual Fund Performance with Learning across Funds.” Journal of Financial Economics 78 (3): 507–552.

[26] Jorion, P. 1985. “International Portfolio Diversification with Estimation Risk.” Journal of Business 259–278.

[27] Jorion, P. 1986. “Bayes-Stein Estimation for Portfolio Analysis.” Journal of Financial and Quantitative Analysis 21 (3): 279–292.

[28] Jorion, P. 1991. “Bayesian and CAPM Estimators of the Means: Implications for Portfolio Selection.” Journal of Banking and Finance 15 (3): 717–727.

[29] Kinnel, R. 2010. “How Expense Ratios and Star Ratings Predict Success.” https://www.morning-star.com/articles/347327/article.

[30] Kircher, F., and D. Rösch. 2021. “A Shrinkage Approach for Sharpe Ratio Optimal Portfolios with Estimation Risks.” Journal of Banking and Finance 133: 106281.

[31] Kosowski, R., A. Timmermann R. Wermers, and H. White. 2006. “Can Mutual Fund “Stars” Really Pick Stocks? New Evidence from A Bootstrap Analysis.” The Journal of Finance 61 (6): 2551–2595.

[32] Kroll, Y., H. Levy, and H. M. Markowitz. 1984. “Mean-Variance versus Direct Utility Maximization.” The Journal of Finance 39 (1): 47–61.

[33] Ledoit, O., and M. Wolf. 2004. “Honey, I Shrunk the Sample Covariance Matrix.” The Journal of Portfolio Management 30 (4): 110–119.

[34] Ledoit, O., and M. Wolf. 2017. “Nonlinear Shrinkage of the Covariance Matrix for Portfolio Selection: Markowitz meets Goldilocks.” The Review of Financial Studies 30 (12): 4349–4388.

[35] Ledoit, O., and M. Wolf. 2020. “The Power of (Non-) Linear Shrinking: A Review and Guide to Covariance Matrix Estimation.” Journal of Financial Econometrics Vol (Issue): pages?

[36] Lee, P. M. Bayesian Statistics. London: Oxford University Press. 2012.

[37] Levi, Y., and I. Welch. 2017. “Best Practice for Cost-of-Capital Estimates.” Journal of Financial and Quantitative Analysis 52 (2): 427–463.

[38] Levy, H., E. G. De Giorgi, and T. Hens. 2012. “Two Paradigms and Nobel Prizes in Economics: A Contradiction or Coexistence?” European Financial Management 18 (2): 163–182.

[39] Levy, H., and M. Levy. 2004. “Prospect Theory and Mean-Variance Analysis.” Review of Financial Studies 17 (4): 1015–1041.

[40] Levy, H., and H. M. Markowitz. 1979. “Approximating Expected Utility by A Function of Mean and Variance.” The American Economic Review 69 (3): 308–317.

[41] Levy, M. 2023. “The Deadweight Loss of Active Management.” The Journal of Investing, forthcoming. Levy, M., and R. Roll. 2016. “Seeking alpha? It’s A Bad Guideline for Portfolio Optimization.” The Journal of Portfolio Management 42 (5): 107–112.

[42] ——. 2018. “Generalized Performance Measures: Optimal Overweighing of Fees Relative to Sample Returns.” The Journal of Portfolio Management 44 (3): 66–75.

[43] Rachev, S., T. Jašic ́, S. Stoyanov, and F. J. Fabozzi. 2007. “Momentum Strategies Based on Reward–Risk Stock Selection Criteria.” Journal of Banking & Finance 31 (8): 2325–2346.

[44] Sharpe, W. F. 1966. “Mutual Fund Performance.” The Journal of Business 39 (1): 119–138.

[45] ——. 1994. “The Sharpe Ratio.” The Journal of Portfolio Management 21 (1): 49–58.

[46] ——. 1998. “Morningstar’s Risk-Adjusted Ratings.” Financial Analysts Journal 54 (4): 21–33.

[47] Wang, Z. 2005. “A Shrinkage Approach to Model Uncertainty and Asset Allocation.” Review of Financial Studies Vol. (Issue): 673–-75.

[48] Zheng, L. 1999. “Is Money Smart? A Study of Mutual Fund Investors’ Fund Selection Ability.” The Journal of Finance 54 (3): 901–933.

风险提示：文献中的结果均由相应作者通过历史数据统计、建模和测算完成，在政策、市场环境发生变化时模型存在失效的风险。