日内跳价风险和股票横截面收益:以中国市场为例
导读
作为西学东渐——海外文献系列报告第一百五十三篇,本文推荐了Haigang Zhou和John Zhu于2011年发表的论文《Jump risk and cross section of stock returns: evidence from China’s stock market》。
目前,各种研究已经证实了不同金融市场中跳价的存在。然而,鲜有学者对跳价风险和横截面上预期股票收益之间的动态关系方面有着较深的研究。本文遵循一个基于随机贴现因子(SDF)的典型的扩散-跳跃模型来研究横截面预期超额收益和不同股票跳价强度之间的关系。在不考虑成本的投资组合中,利用跳价强度构建的最高和最低十分位数投资组合之间的年化收益差高达24%,年化夏普比率为1.67。Fama-MacBeth检验表明,即使在控制了其他共同的风险因素之后,股票超额收益在跳价强度上也是单调下降的。
风险提示:文献中的结果均由相应作者通过历史数据统计、建模和测算完成,在政策、市场环境发生变化时模型存在失效的风险。
1、引言
自Press(1967)、Merton(1976)、Cox和Ross(1976)以来,金融学相关文献一直强调将突然的、不经常发生的、但往往是剧烈的价格运动纳入资产定价模型的重要性。过往的研究已经证明了跳价在投资组合和风险管理、期权和债券定价以及对冲等方面的巨大影响。本文我们引入一个基于随机贴现因子(SDF)的扩散-跳跃模型,来研究预期超额收益和跳价强度之间在横截面上的动态关系。其中,后者是公司面临跳价风险的代理变量,定义为每月的日度绝对跳价收益之和。通过使用中国A股市场的高频交易数据,本文提供了基于新兴市场得到的实验结果,这是对主要集中于美国市场的现有文献的补充。
在本文中,我们应用Yan(2008)的连续时间模型框架来实证检验跳价风险的系统性特征,并拆分出跳价所带来的风险溢价。该模型假设随机贴现因子和股票价格遵循相关的扩散-跳跃过程,模型由布朗运动和泊松过程组成。预期的超额股票收益由这两个来源的系统性风险补偿:即随机贴现因子和股票价格的布朗运动之间的协方差而产生的扩散分量,以及当随机贴现因子和股票价格的泊松过程相互依赖时的跳价分量。当且仅当跳价风险是非系统性的(即SDF的泊松过程和股票价格的泊松过程是不相关的),预期超额收益的部分横截面变化可以由股票的跳价特征来预测。该模型的一个含义是,如果SDF的平均跳价幅度是正的,那么预期超额收益在股票的跳价强度中是单调递减的,其他情况下也是如此。我们进一步测试了横截面下的简单投资策略的盈利能力。
对跳价的准确检测和对其大小的具体估计是衡量跳价强度的关键。在我们的实证分析中,跳价强度的估计是至关重要的。目前已有一系列的研究提出了各种方法来检测跳价的到来和衡量已实现的跳价幅度。其中,我们采用了Lee和Mykland(2008)提出的非参数方法。他们的非参数检测方法可以精确识别跳价发生的时间间隔,并允许在一个交易日内多次发生跳价。此外,为了获得针对跳价频率和跳价幅度的联合估计,Lee和Mykland的方法与其他研究中提出的方法相比,更加直接和直观。
我们基于高频交易数据,对2003年1月至2008年9月在上海证券交易所交易的每只A股股票采用Lee和Mykland的跳价检测方法。对于每只股票,我们确定了跳价的日内间隔,计算了间隔内的跳价收益,并定义了月度累计绝对跳价收益,作为跳价强度的代理变量,该变量包含股票的平均跳价幅度和跳价频率的相关信息。然后,我们构建了按跳价强度排序的十等分(或五等分)的投资组合,并设置调仓频率为月度。基于Fama-MacBeth测试提供了强有力的证据以支持股票组合中存在系统性的跳价风险。这证实了我们的观点,即预期超额股票收益在跳价强度中单调递减。一个利用最高和最低十分位数投资组合之间收益率差的零成本投资组合可以获得高达24%的年化收益,年化夏普比率为1.67。在考虑了一系列股票特征变量(包括市场风险、已实现和特异性收益、规模、账面市值比、滞后波动率、周转率和非流动性)后,该测试结果同样是稳健的。
本文的结构如下:在第2节中,我们构建理论模型,并推导出可检验的含义,并简要介绍了检测跳价和估计跳价幅度的方法。第3节详细介绍了变量和测试组合的构建方式。在第4节中我们提出实证结果,并在第5节中得出结论。
2、方法论介绍
2.1
跳价和资产定价
我们遵循Yan(2008)的连续时间模型方法,为随机贴现因子和股票价格构建扩散-跳跃过程。我们将M(t)定义为具有正随机过程的随机贴现因子(SDF),其中MSi是第i个股票价格过程Si(t)的鞅。例如,M是基于CAPM中代表投资者的时际边际替代率。下述特性
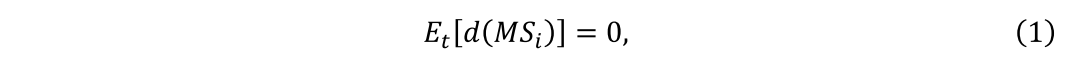
表明边际效用加权价格为鞅,其中Et[.]是时间t下的条件期望值。大多数现有的资产定价模型都可以统一在该随机贴现因子框架下(例如,见Cochrane 2005)。因此M(t)和Si(t)遵循以下扩散-跳跃过程。

在将布朗运动和泊松过程分解为共同分量和特异性分量后(详见Yan 2008),我们基于SDF和股票价格过程给出另一种针对MSi应用伊藤公式的表达式,为:
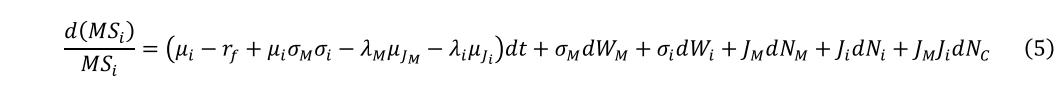
其中NC是在泊松过程中的分项,是驱动NM和Ni的共同因素。利用公式1,JM(i)的对数正态性,以及一些近似计算,我们得到了资产定价方程,它是我们后续实验分析的基础。
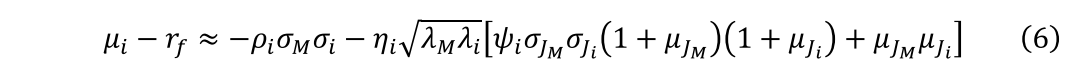
公式左侧为股票i的超额收益。公式右侧是预期收益在离散时间β下的表示的连续时间近似值。如果股票收益的扩散过程dWi与SDF的扩散过程dWM负共变,预期的股票收益必须高于无风险利率(ρi<0);那么在离散时间框架中,正的预期超额收益来自于正值β,而β又是SDF和股票收益之间负共变的表征。在公式6中,预期的超额股票收益不仅取决于连续样本路径的风险溢价,而且关键取决于资产价格中不连续/跳价分量所驱动的溢价(或折价)。尤其是,如果跳价存在但不是系统性时(ηi=0),就像Merton(1976)所说的那样,公式6中的第二项就会完全消失,因此,预期股票收益不会对特异性跳价风险进行补偿。
当系统性跳价风险存在时(ηi=>0),除了市场β外,公式右侧上括号内的两个分量共同决定了股票超额收益的大小。第一个分量的正负号取决于ψi,即M和Si的跳价幅度的相关系数。如果股票的跳价大小与SDF的跳价大小呈负相关,那么预期超额收益就会更高,反之亦然。在ψi=0的特殊情况下,第二部分对预期超额收益的解释在公式6的简化版本中将会被突出:
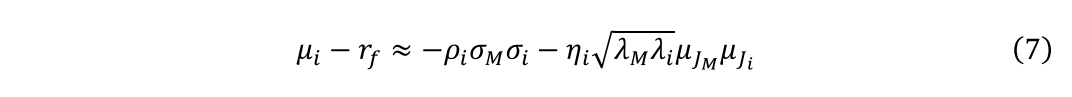
公式7表明,如果股票的跳价大小与M的跳价大小不相关(即ψi=0),但股票平均跳价大小的正负号与SDF平均跳价大小的正负号相反(即μJMμJi<0),该股票会获得更高的收益,反之亦然;此外,如果股票的平均跳价大小与M的平均跳价大小的正负号相同,则预期超额收益将被抑制或降低,反之亦然。为了从公式7中找出一个可测试的假设,即与跳价风险的横截面变化有关的横截面预期超额收益的可预测性,必须确定参数μJM的符号。根据现有的资产定价模型(详见Bakshi等1997;Bates 2000;Pan 2002;Eraker等2003;Rietz 1988;Barro 2006;Yan 2008),平均SDF跳价规模的符号为正,μJM>0。因此,我们可以提出以下假设:
假设1:如果平均SDF的跳价幅度为正,那么当股票的跳价幅度与SDF之间的相关性为零时,超额股票收益在跳价强度中单调递减,跳价强度由平均跳价大小(μJi)与跳价频率(λi)共同决定。
根据公式7,我们提出以下Fama-McBeth回归来检验以验证上述假说。
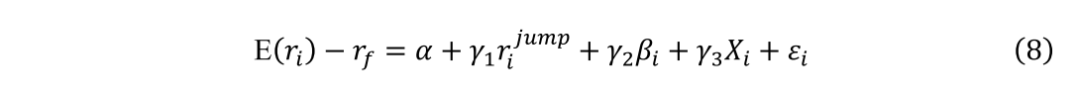
其中,rijump是跳价强度的代表,代表公式7中的sqrt(λi)μJi,而Xi是一组控制变量,例如,市值、成交量、非流动性等(详见第3.2节)。我们在第2.2节中详细介绍了识别和估计股票特定跳价参数λi和μJi的实证策略。请注意ηi也共同决定了公式7中的股票超额收益,但在我们的实证分析中,每只股票的超额收益仍未被观察到。因此,公式8不适合直接应用于股票横截面。然而,假设ηi、μJi和λi在不同的股票中是独立的情况下,我们可以很容易地将投资组合中ηi的平均值与按跳价强度排序的每个分散的投资组合中μJi和λi乘积的平均值分开。如果投资组合规模足够大,ηi的投资组合均值就会收敛到ηi的总体均值。因此,当测试资产是投资组合而不是单个股票时,ηi在各投资组合中成为一个常数,这验证了公式8中的说法。
2.2
识别和测量跳价
假设市场上出现了一个跳价,并影响了tτ时刻的股票价格,那么tτ时刻的已实现资产收益一定比通常情况下要高得多。然而,高于常规的收益不仅是由跳价引起的,也是由完全归因于价格过程中连续样本路径的高波动性引起。为了在统计上区分由跳价引起的高于平常的已实现收益和那些与跳价无关的高波动率,我们基于Lee和Mykland(2008)使用已实现收益与瞬时波动率的比率,σ(tτ)来检测跳价,该比率是由价格过程的连续部分的局部运动估计出来的。
Lee和Mykland(2008)提出了以下统计量来检测从tτ-1到tτ中是否发生跳价:
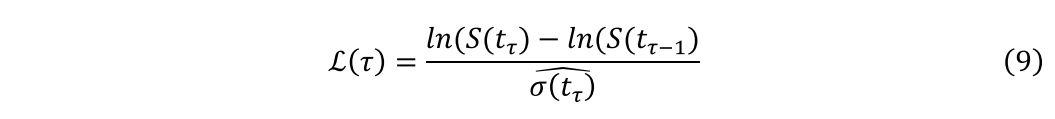
其中S(t)是t时刻的资产价格,且遵循公式3中描述的扩散-跳跃过程。σ(tτ)是瞬时波动率的一致估计量,即使在以前的时间段存在跳价现象。
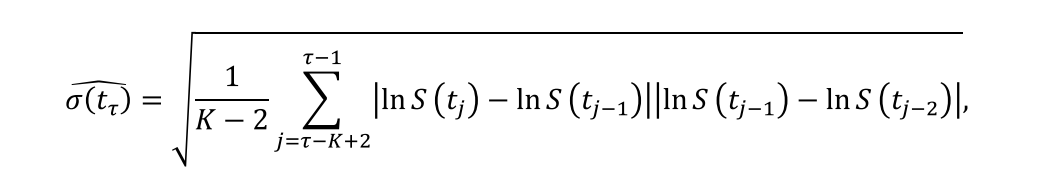
其中K是时间窗口的大小,在此范围内考虑价格过程的相应局部运动。随着窗口大小K的增加,跳价对估计波动率的影响也会减弱。Lee和Mykland(2008)表明,在任何任意小的区间(tτ-1, tτ]内,在没有跳价的情况下,L(τ)的最大值具有以下极限分布。

在下面的实证分析中,我们基于Lee和Mykland方法,对上海证券交易所所有A股股票的15分钟高频数据进行分析。根据Lee和Mykland(2008)的相关建议,我们在估计瞬时波动率时将窗口大小K设为156。

3、数据、变量构建和投资组合和策略的构建
我们从分析师数据库(The Analyst Database)中收集了2003年1月至2008年9月在上海证券交易所交易的所有A股股票的高频交易数据。为了避免可能影响结果的市场微观结构噪音,我们将原始数据转化为15分钟的收益率进行实证分析。Lee和Mykland(2008)的研究表明,该测试对15分钟间隔的微观结构噪音是稳健的。
与纽约证券交易所不同的是,上海证券交易所在一个交易日内的交易时间有两个时段:上午9:30至11:30以及下午1:00至3:00,其中间有一个午休。因此,一个交易日的第一个15分钟对数收益是根据上午9:30:01至9:45:00之间的交易价格计算的,而上午时段的最后15分钟对数收益是在上午11:15:01至11:30:00之间。下午时段观察到的第一个对数收益是在1:30:01 PM到1:45:00 PM之间,最后一个是在2:45:01 PM到3:00:00 PM之间。在一个交易日中,我们最多可以观察到16个15分钟收益,前提是每个15分钟的间隔中至少有一次交易。我们将非交易区间的收益视为缺失值,并将其排除在我们的分析之外。
我们进一步将样本限制在那些至少有10个15分钟收益样本点的交易日,以尽量减少不频繁交易对我们的结果产生影响。为了消除首次公开募股后几天内的不规则和极端的价格波动,我们排除了每只股票首次出现在数据集中的前22个交易日。最后,我们采用“夹层过滤法”来剔除绝对收益大于10%的交易日,因为它与上海证券交易所现行的涨跌停限制相冲突。
3.1
基于投资组合构建策略
在t月初,我们按照t-1月的跳价强度对股票进行升序排序,并将它们分成同等权重的五分位数或十分位数投资组合。我们在t月初买入这些投资组合,并在t月底卖出。我们每月重复这一过程,以获得同等权重的投资组合收益的时间序列。我们还构建了一个零跳价组合,其中包括前一个月没有发现跳价的股票。因此,我们总共有六个或十一个按跳价强度排序的等权测试组合。
为了控制其他可能预测截面收益的解释变量,我们采用Fama和French(1993)的双重排序方法来建立5×6的投资组合。我们首先利用其他解释变量将股票分配到五个五分位数组合中,然后根据跳价强度将每个五分位数中的股票分为六个组合。
3.2
变量构造
我们从CSMAR数据库中获得每月的市值(ME)和市值账面比(MB),其中股权的账面价值是不含少数股东和少数股东权益之和。两者都是在每个月的月底计算。按照Amihud(2002)的说法,流动性不足(ILLIQ)是由每月平均的每日股票绝对收益与每日交易量的比率来计算。股票周转率(TO)是一个月内的总交易额除以市值。市场β是通过股票收益率对上海证券交易所A股指数前48个月收益率的滚动回归来估计的。已实现收益率rt-1是构建该投资组合的当月股票收益率。已实现特异性收益被定义为ridio=r-βRM,其中RM是持有月份的上海证券交易所A股指数的收益。
我们从RESSET/DB数据库中获得中国市场的Fama-French三因子模型的数据。SMB是三个小市值组合的平均收益减去三个大市值组合的平均收益:SMB=1/3(小市值价值+小市值中性+小市值成长)-1/3(大市值价值+大市值中性+大市值成长)。HML是两个价值投资组合的平均收益减去两个成长投资组合的平均收益:HML=1/2(小市值价值+大市值价值)-1/2(小市值成长+大市值成长)。R_M-R_f,市场的超额收益,是所有A股的估值加权回报(来自CSMAR)和三个月银行存款利率(来自中国中央银行、中国人民银行)之间的差额。
4、实证结果
4.1
跳价统计说明
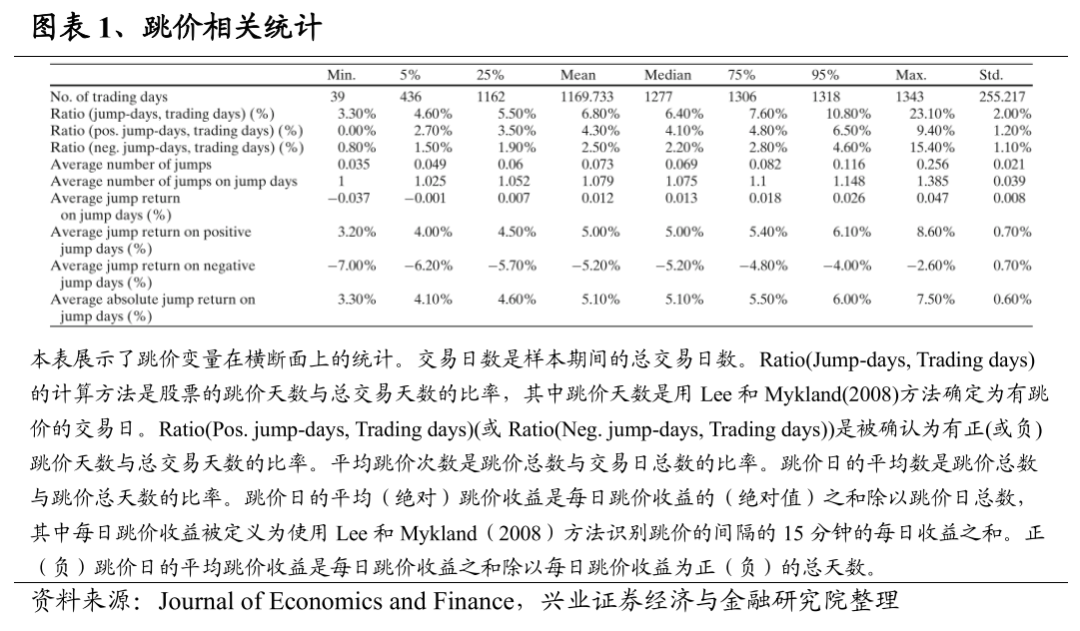
图表1展示了2003年1月至2008年9月期间在上海证券交易所(SSE)交易的所有A股股票的跳价相关变量的汇总统计。我们使用Lee和Mykland(2008)的方法在1%的显著性水平上识别股票是否出现跳价。
该表证实了跳价是相对罕见的事件。在任何给定的交易日,一只普通股票有6.80%的机会出现价格跳跃。该表表明,跳价的频率在横截面有着相当大的差异。在上海证券交易所的所有交易日中,最低3.30%和最高23.10%的个股出现跳价。上交所A股跳价频率在截面的平均值远低于12.07%,即Dunham和Friesen(2007)测试的标普100股票跳价频率的截面平均值。Zhou和Zhu(2009b)(图表2 A部分)展示了在上海证券交易所上市的50只市值最大的A股股票的平均跳价频率为7.79%。对于一只相对典型的股票来说,正的价格跳跃,即被定义为导致正向盘中区间收益的价格跳跃,比负的跳价更经常发生,在所有交易日中的占比分别是4.30%和2.50%。平均来说,正向跳价给股票带来了5.00%的日度价格上涨,而负向跳价则导致了5.20%的价格下跌。这些结果表明,跳价对股票收益产生了不对称的影响。尽管负向跳价发生的频率较低,但它们通常会导致更大的价格影响。大多数股票在每个交易日最多出现一次跳价,平均而言,在跳价出现的交易日内有1.08次跳价。
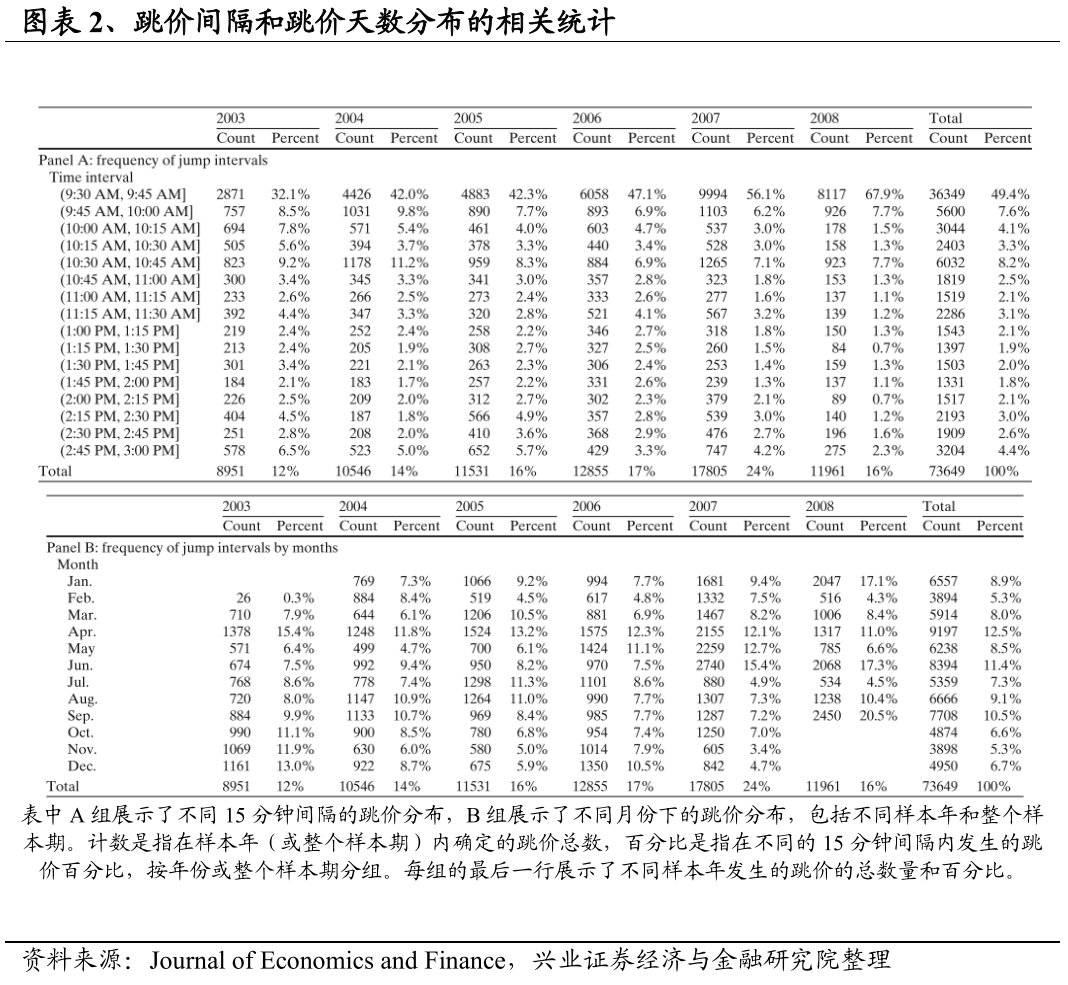
图表2在A组中展示了日内跳价分布,在B组中展示了的跳价的不同月份下的分布统计。结果表明,股票价格的跳价绝大部分是在开市前后出现的。平均来说,49.4%的跳价是在开市后的第一个15分钟的时间段内出现。这一发现与Lee和Mykland(2008)的研究相似,后者发现73%的跳价在开市后的第一个15分钟内出现。跳价在第一个15分钟的时间段内出现的概率是一个上升趋势,从2003年的32.1%到2008年的67.9%。图表2的B组表明,没有明显的证据表明不同月份的跳价频率是有季节性。唯一的例外是4月:从2003年到2006年,它占了跳价次数的最高部分。4月份跳价相对集中可能是由于所有A股上市公司必须在4月30日前提交年度报告导致的(Haw等人,2006)。
4.2
投资组合表现
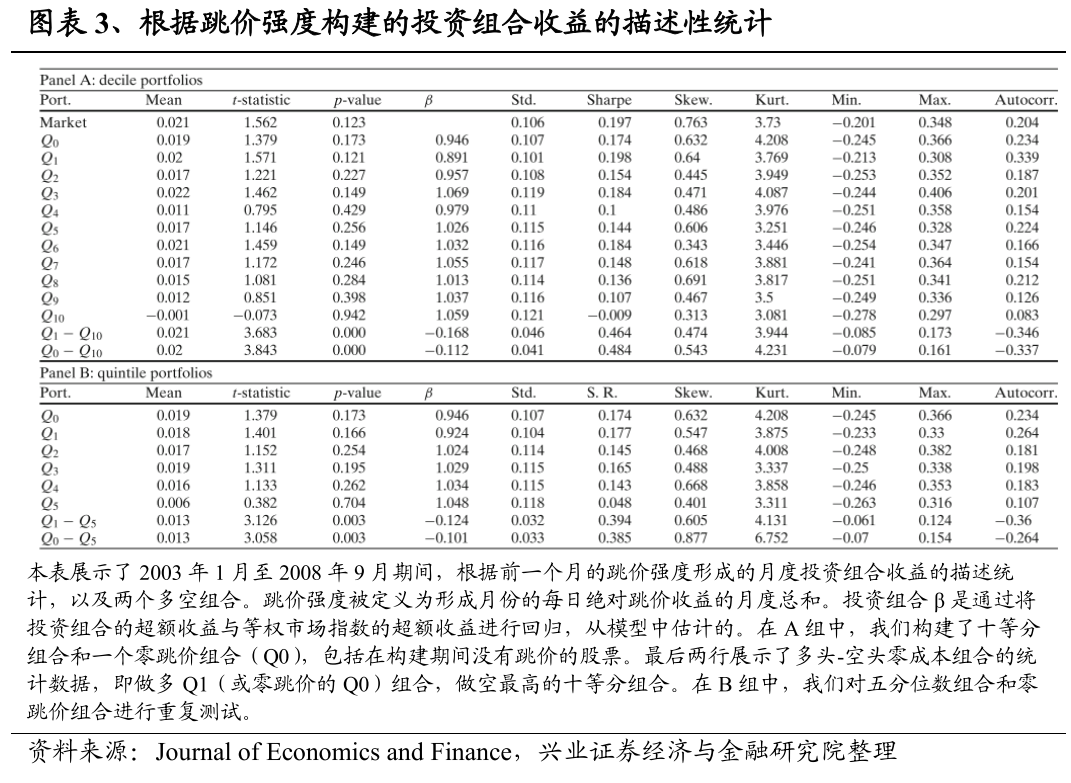
图表3展示了十等分和五等分投资组合以及两个多空投资组合的月度收益汇总统计,这些投资组合是根据跳价强度构建的,其中跳价强度被定义为前一个月的日度绝对跳价收益月度总和。A组表明,没有一个十等分组合产生明显的收益。所有的十等分组合都是左偏和厚尾的。然而,多空十等分组合,Q1-Q10,产生了2.1%的明显正月均收益(年化收益率为28.3%),月度夏普比率为0.464(年化为1.67)。五分位数组合在B组中表现出非常相似的特征。多空五分位数组合,Q1-Q5,产生了1.3%的月度收益(年化收益率为16.8%)。我们还研究了持有零跳价组合并做空最高分位数(五分之一)组合的交易策略的盈利能力。零跳价组合包括所有在某月没有经历跳价的股票,并且每个月都会重新平衡。平均来说,多头-空头策略,Q0-Q10和Q0-Q10,分别产生了26.82%和16.82%的年化收益率。这些发现与Yan(2008)针对美国市场的研究相似,后者在交易策略上与我们相似。
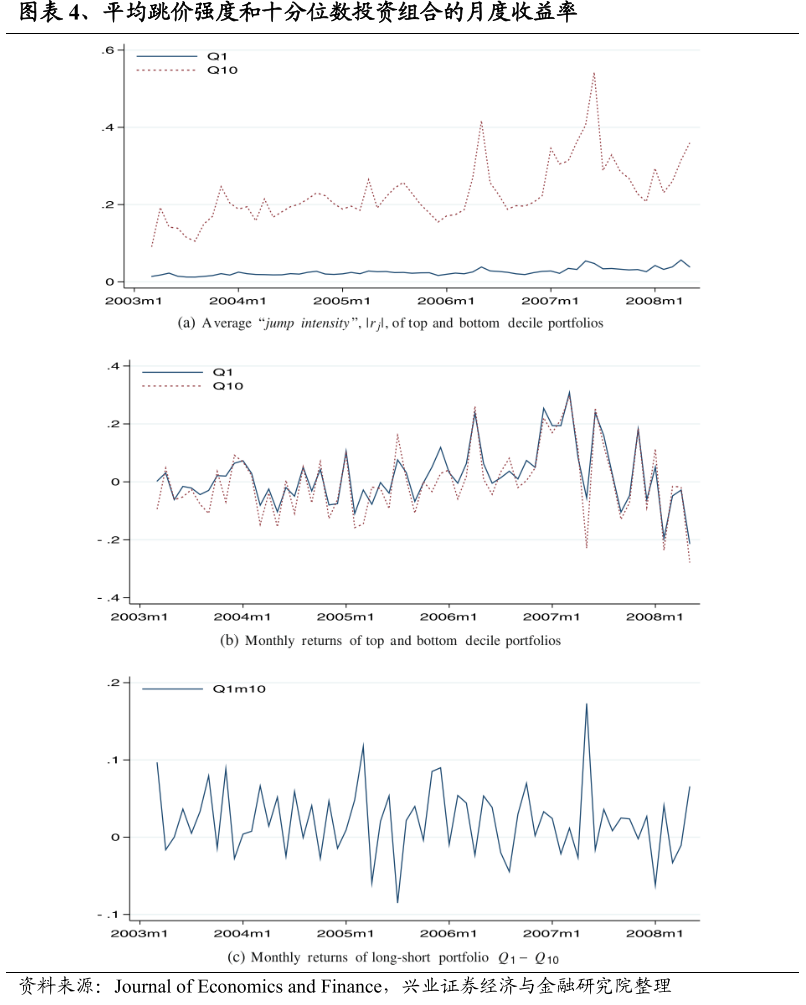
我们在图表4的(a)部分绘制了两个十等分组合的月度跳价强度的组合均值。很明显,在样本期间,Q10组合的跳价强度的组合均值总是明显高于Q1组合。(b)部分绘制了最高(Q10)和最低(Q1)十分位数组合的月度收益率。两个十等分投资组合的收益率大部分情况下是一起变动的,但最低的十等分组Q1的收益率在2/3的交易月中高于最高的十等分组Q10。(c)部分绘制了多空组合(Q1-Q10)的月度收益率,其中最高(最低)月度收益率为17.3%(-8.5%)。(c)部分还展示了在样本期间,多空组合经历了不超过两个月的连续亏损,并且遭受了不超过8.5%的最大累计损失。
4.3
控制其他变量后的投资组合表现
跳价强度有可能与其他风险因子有关,因此,图表3中发现的显著的多空组合收益反映了跳价风险以外的风险因子导致的风险溢价。为了分离跳价风险对资产定价的影响,我们首先根据其他解释变量将股票分为五个组合。然后,在每个投资组合中,我们按照跳价强度对股票进行排序,并将其分为五个子投资组合,外加一个零跳价投资组合。我们总共得到了30个投资组合。如果其他风险因子能解释我们在表3中发现的显著的多空组合收益,我们会发现在按其他风险因子排序的每个五分位数组合中,低跳价强度和高跳价强度的组合之间没有显著的收益。我们在控制了一些常见的风险因子,包括市场风险(β)、已实现收益(rt-1)、已实现特异性收益(ridio)、市值(ME)、市值账面比(MB)、滞后波动率(σ(rt-1))、股票周转率(TO)和非流动性(Illiq.)之后,重新计算了图表3的结果,并在图表5中展示结果。
4.4
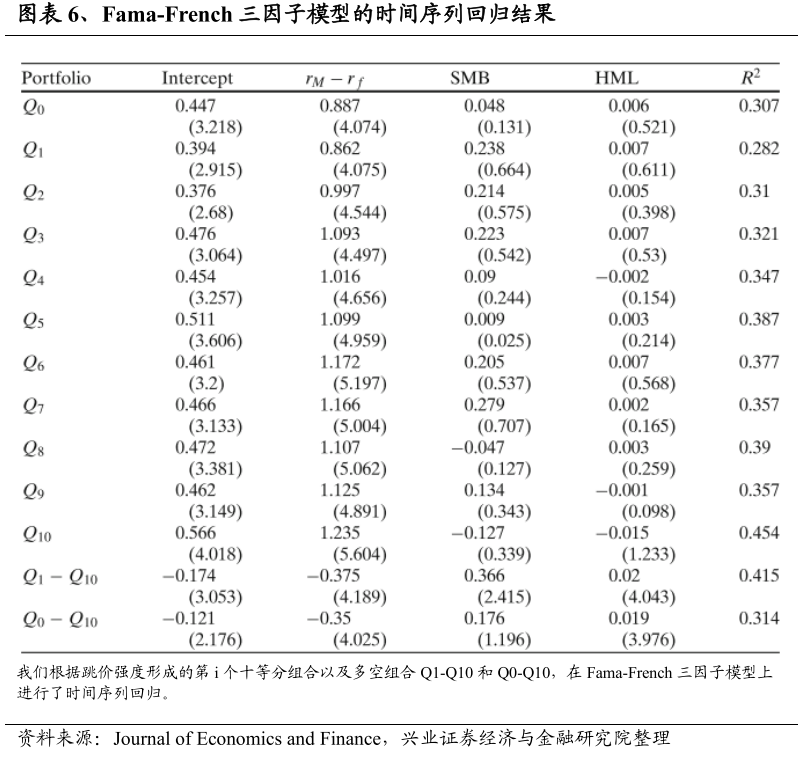
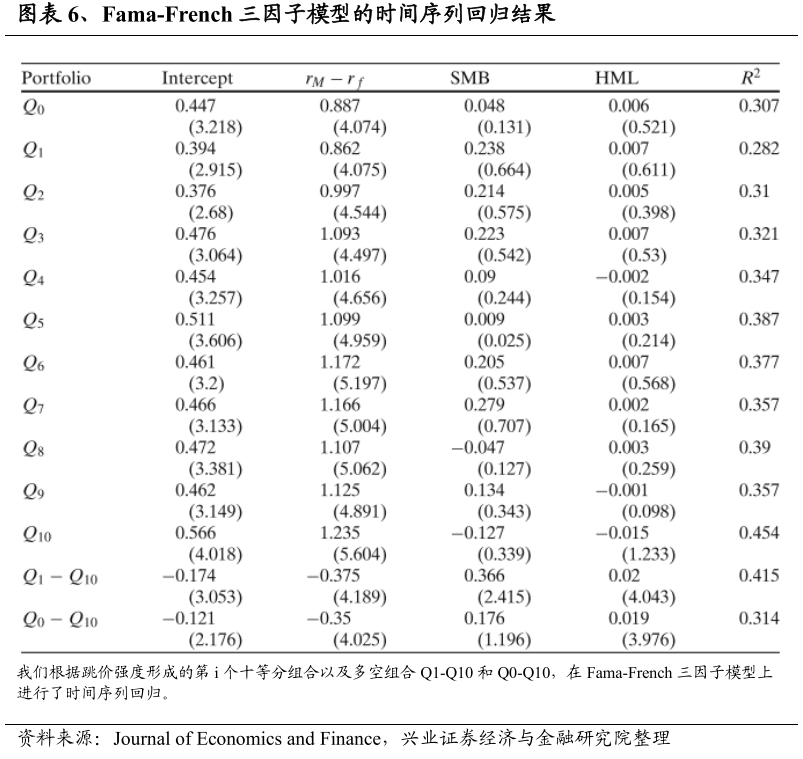
Fama-French三因子模型和二十五个Fama-French投资组合
我们接下来研究多空组合的正收益是否可以用资产定价模型来解释,特别是用Fama-French三因子模型。如图表6所示,所有11个投资组合的rM-rf的估计系数都是显著的,而SMB和HML的负载与0值没有明显的区别。所有的时间序列回归的截距都是显著为正。毫不奇怪,在Gibbons等人(1989)的F检验下,所有11个投资组合的截距共同为零的假设被强烈拒绝,P值为0.000%。此外,三因子的解释力在第一个十分位数组合中为28.2%,在第十个十分位数组合中为45.4%。
4.5
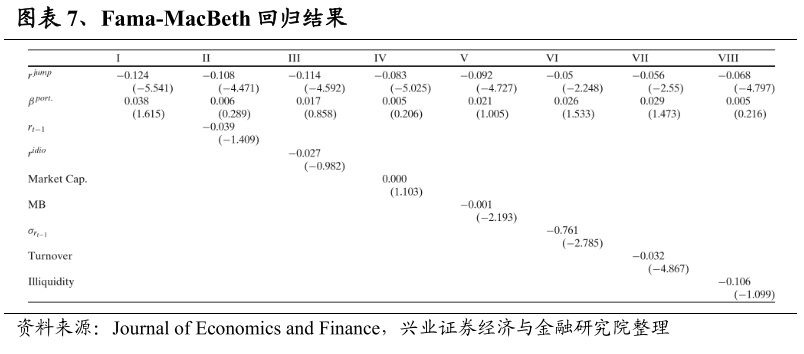
Fama-MacBeth回归
图表7展示了公式8中设定的Fama-MacBeth横截面回归模型的结果。在图表7的模型一中,我们只针对跳价强度上构建了11个测试组合。在模型II-VIII中,我们基于控制变量,并根据跳价强度构建了30个测试组合。控制变量包括已实现收益率(rt-1)、已实现特异性收益率(ridiot-1),市值(ME),市值账面比(MB),滞后波动率(σ(rt-1)),股票周转率(TO)和非流动性(Illiq.)。
每个月,我们按照Fama和MacBeth(1973)的方法,将等权的投资组合超额收益与股票特征进行回归,如公式8所设定。横截面回归每个月重复进行,共记63个月。进一步,我们计算出跳价强度、市场风险和股票特征变量的估计回归系数γ的时间序列平均值,并通过均值为零的T检验来检验其是否显著。
在模型一中,rjumpi的系数,表示为γ1,其统计意义上的平均值为-0.124(t=-5.541),中位数为-0.102。该结果强烈支持跳价强度是显著的,与超额股票收益在跳价强度中单调递减的假设一致。序列γ1的自相关性为-0.113,可以忽略不计。市场风险的正系数β与CAPM一致。
公式8中设定的(即控制了额外的风险因子)横断面模型的估计结果展示于图表7的其余各列(模型II-VIII)。rjumpi的系数仍然是负的,并且在常规的显著性水平上测试结果为显著,不管回归中包括哪些了控制风险因素。
正如预期的那样,市场风险的系数β是正的,而且是显著的。然而,当把已实现收益率、已实现特异性收益率、市值、市值账面比或非流动性作为控制变量时,它变得不显著。已实现收益率的系数显著为负,这与反转策略在中国股票市场的短周期内有利可图的结论相一致。此外,市值账面比、滞后波动率和周转率的系数都是显著的负值。
上述结果支持了这样一个假设,即用跳价强度衡量的跳价风险是系统性的,并且在市场横断面上是被充分定价的。这些结果在控制了其他风险因素后依旧稳健。
5、总结
在本文中,我们基于实证得到了强有力的证据,表明横截面的预期股票收益与用跳价强度衡量的跳价风险的变化有关。基于一个典型的扩散-跳跃模型,该模型允许SDF和股票价格中跳价动态存在依赖性,我们检验了关于不同股票的跳价强度如何系统地解释预期超额收益在横断面上的变化这一假设。
为了实证检验这一假设,我们基于Lee和Mykland构建的非参数跳价检测方法来确定价格跳价到达的日内区间,并联合估计了跳价频率和每日跳价收益率。通过使用中国股市的高频交易数据,我们发现跳价是相对罕见的事件,平均发生在6.8%的交易日,与之前美国数据的经验发现一致。我们还发现,大约有一半的跳价事件是在开盘后的前15分钟内发生,而跳价事件的发生在每年的不同月份里没有明显的规律。
然后,我们根据跳价强度构建了十等分和五等分投资组合,其中跳价强度被定义为每月的日度绝对跳价收益之和。平均来说,做多最低的十等分(五等分)投资组合和做空最高的十等分(五等分)投资组合的交易策略产生的年化收益率为28%。一个做多零跳价投资组合的交易策略(即包括所有在特定月份没有经历过跳价的月度调仓等权股票组合),以及做空最高十分位数(五分位数)的投资组合,在样本期间产生类似于上述大小的收益。接下来,我们研究了超额跳价收益是由其他风险因子导致的可能性,包括市场风险、已实现收益、已实现特异性收益、市值、市值账面比、滞后波动率、股票周转率和非流动性。我们用其中一个风险因子和跳价风险组成30个双排序的投资组合,并重新测试多空组合收益的显著性。证据显示,在控制了各种风险因子后,做多最低跳价五分位数组合和做空最高跳价五分位数组合的交易策略所获得的超额收益仍然显著为正。上述结论得到了Fama-MacBeth分析的证实。在控制了各种风险变量后,跳价变量仍然是决定11个单一分类组合超额收益的重要因素。基于Fama-Frech三因素模型的分析表明,多空策略的超额收益不能由市场超额收益、规模或价值因素来解释。
风险提示:文献中的结果均由相应作者通过历史数据统计、建模和测算完成,在政策、市场环境发生变化时模型存在失效的风险。
参考文献
注:文中报告节选自兴业证券经济与金融研究院已公开发布研究报告,具体报告内容及相关风险提示等详见完整版报告。
证券研究报告:《西学东渐--海外文献推荐系列之一百五十三》
对外发布时间:2023年2月23日
报告发布机构:兴业证券股份有限公司(已获中国证监会许可的证券投资咨询业务资格)
--------------------------------------
分析师:郑兆磊
SAC执业证书编号:S0190520080006
E-mail: [email protected]
--------------------------------------
更多量化最新资讯和研究成果,欢迎关注我们的微信公众平台(微信号:XYQuantResearch)!


本篇文章来源于微信公众号: XYQuantResearch