【浙商金工】量化投资算法前瞻:强化学习


摘要
01
导读
1.1. AlphaGo取胜围棋冠军,强化学习进入大众视野
2016年,AlphaGo以4:1的成绩胜过[文]世界围棋冠军李世石。不久之后的2017年,A[章]lphaGo在中国乌镇围棋峰会上与世界围棋冠[来]军柯洁对战,以3:0总分获胜。AlphaGo[自]的胜利标志着深度强化学习算法在围棋AI方面所[1]取得的惊人成绩,深度强化学习获得了广泛关注,[7]也引发了人们对于通用人工智能的思考与探索。
围棋AI(AlphaGo)背后所使用的算法,创新性地结合了深度强化学习和蒙特卡洛树搜索,通过策略网络选择落子位置,而使用价值网络评估棋盘局面,搜索效率大幅提升,胜率估算更加精确。此外,AlphaGo使用强化学习的自我博弈来实现策略网络的学习以改善其性能,还通过自我博弈和快速走子结合形成棋谱数据进一步训练价值网络。本文将在第2章中具体介绍强化学习算法,对策略、价值等术语和相应的网络进行解释。
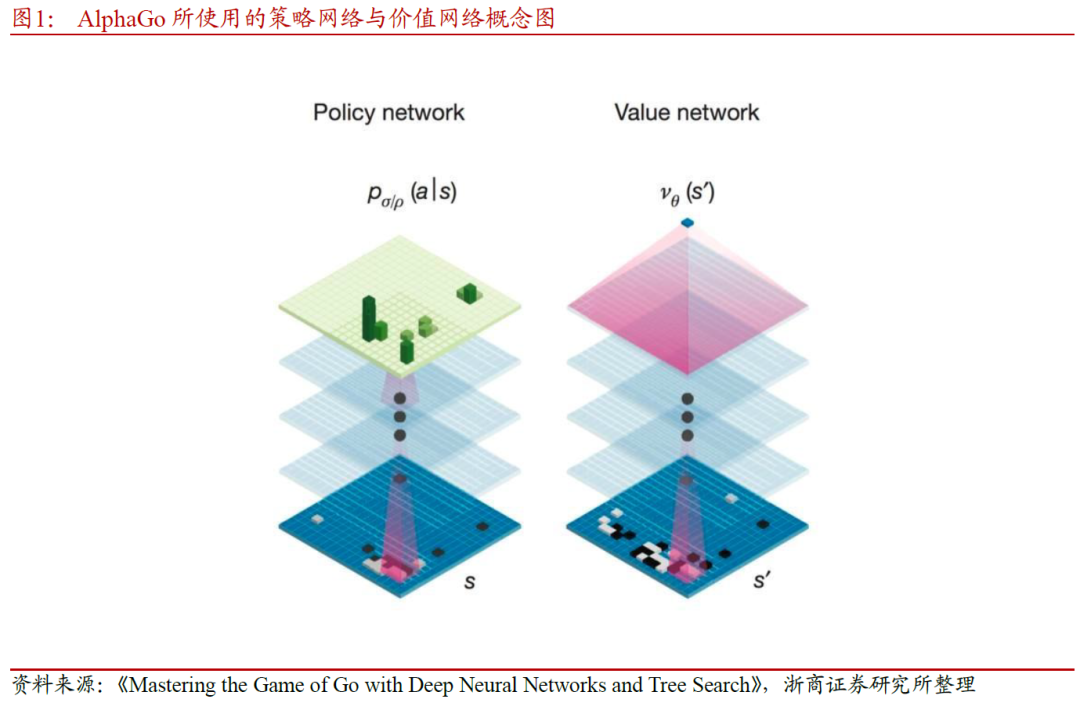
AlphaGo的面世为强化学习研究带来了学界和业界的广泛关注,加速深度强化学习研究领域的发展,其理论和应用得到了逐渐完善。在大规模计算的任务中,深度强化学习智能体展示了卓越的进步。研究人员在基于值函数和基于策略梯度的深度强化学习算法方面都取得了一系列的研究成果。深度强化学习的研究一方面可以提升各种复杂场景中智能体的感知决策能力,另一方面,高效算法的应用落地也体现在多个行业及领域,如医疗、智能驾驶、推荐系统等。
1.1. 市场对于强化学习在投资领域的应用拭目以待
近年来,在电子订单驱动的市场中,关于成交、报[量]价和订单流的大量金融数据的可得性及数据质量快[化]速提高,彻底改变了数据处理和量化建模技术的底[ ]层基础,并带来了新的理论和计算上的挑战。
强化学习带来了新颖的策略优化方法,即在某些系[ ]统中行动的决策者可以通过与系统的互动获得的重[ ]复经验来学习做出最佳决策。当交易者对市场和其[1]他竞争者的信息有限时,使用强化学习算法有利于[7]改善交易决策。在量化投资领域,将强化学习应用[q]于算法交易、做市策略和投资组合管理等领域的研[u]究成果不断推陈出新,获得了广泛关注,市场对于[a]实际应用强化学习算法的策略和产品正拭目以待。[n]
02
从马尔可夫决策过程到强化学习
强化学习有一套完整的框架来定义智能体与环境之[t]间在状态、行动和奖励方面产生的互动。这个框架[.]的目的是以一种简单的方式来表示人工智能问题的[c]基本特征,包括因果关系、不确定性以及明确的优[o]化目标。本章将首先建立起强化学习的术语环境,[m]并介绍算法的数学基础马尔可夫决策过程,以帮助[文]读者理解强化学习的工作原理,再对经典算法及其[章]分类进行说明。
2.1. 建立强化学习的语境
强化学习最大的特点就是在学习的过程中没有标准答案,而是通过奖励信号来学习,这比监督学习更加适应金融市场决策场景,即对于任一交易行为不做标签化的正误判断,而是通过实际获得的收益与风险来实现策略的评估与优化。
在强化学习模型中,产生动作的决策者被称为智能体,智能体依据环境的状态,与环境交互从而决策,做出动作。在传统监督学习体系中,并未对交易决策与市场直接的相互作用进行有效的模拟,而强化学习则充分考虑了两者间的关系。
环境可能存在的状态集合被称为状态空间,而智能体能选取的动作集合被称为动作空间。智能体从动作空间中依据一定的规则选取执行的动作,这种决策规则被称为智能体的策略。
智能体每做出一个动作,都会得到环境相应的反馈,称为奖励。从当前时刻到回合结束的累计奖励记为回报。在任一时刻,智能体与环境交互会产生不同的轨迹,则未来回报具有不确定性,而回报的期望被称为价值。强化学习算法是通过设立恰当的奖励机制,不断优化智能体的策略,从而采取最大化价值的动作。
建立了强化学习的基本语境,本文在 2.2.1节中具体介绍强化学习算法是如何在马[来]尔可夫决策过程中学习外部信息并更新模型参数的[自]。
2.2. 实现强化学习算法
强化学习的基础框架是马可夫决策过程(MDP)[1]。本文利用2.2节从马尔可夫过程到马尔可夫决[7]策过程,再到强化学习是如何在MDP中实现学习[量]和目标优化的,来阐述强化学习的工作原理。
2.2.1. 马尔可夫过程
马尔可夫性假设未来的状态仅仅取决于现在的状态[化],独立于过去的状态,即,当前时刻的状态包含了[ ]此前的全部信息。马尔可夫性又被称为“无后效性[ ]”。
对于一个随机过程, 已知时刻 t 所处的状态 s(t) 仅与 s(t-1) 相关,而与t时刻之前的状态无关,则称这个过程[ ]为马尔可夫过程。
2.2.2. 掌握驱动:累积奖励期望
在智能体与环境通过反馈信号不断进行交互,其最终目的是让智能体最大化累积奖励,即回报,记为G。对于有限时界(finite-horizon)的情况,累积奖励计算如下:
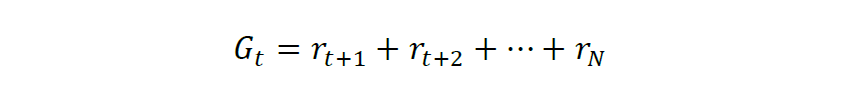
而对于无限时界的情况,则需要引入折现因子的概念,记为 gamma,折现因子是一个略小于但接近1的数,防止没有损耗地积累导致累积奖励目标发散,同时也代表了对未来奖励的不确定性的估计。则在t时刻回报可以表达为结束时的所有奖励折现之和,即:
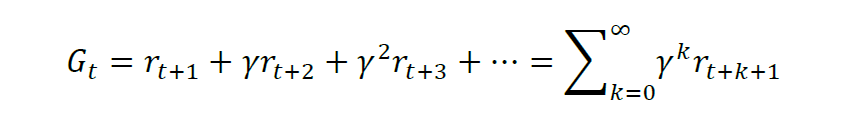
多时候环境状态是不确定的,智能体执行一个动作后会以一定的概率转移到另一个状态,因此得到的奖励也与这个概率相关。所以在计算累积奖励的时候,通常是计算奖励的期望,记为V,则状态s的期望奖励值表示为:
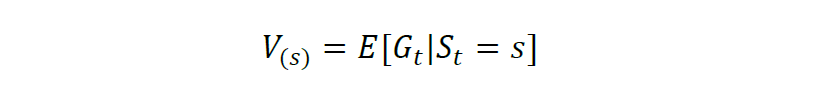
结合无时界累积奖励的表达式,期望奖励可记为:
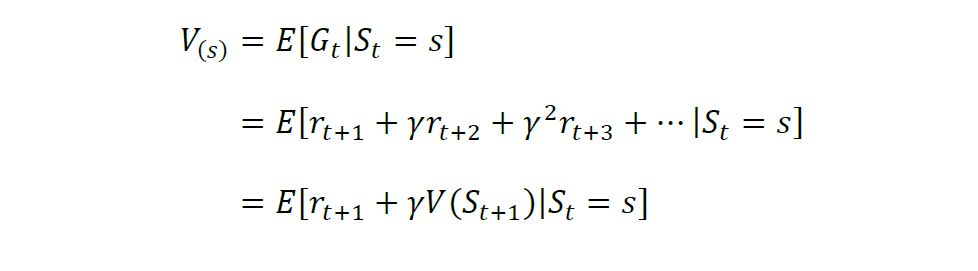
2.2.3. 从马尔可夫决策过程到强化学习
马尔可夫决策过程可定义为一个五元组:M=(S, A, R, P, gamma),变量含义依次为状态空间 S,动作空间A,奖励函数R,状态转移规则P(表示在状态s下,下一个状态为s’的概率)。对于强化学习要学习的策略(pi),则表示了智能体从状态到动作的映射关系,记为:
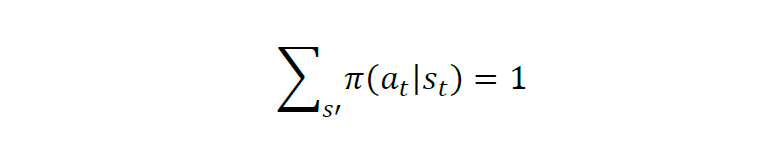
如何衡量策略 pi 的好坏?判断策略的累积奖励的期望值高低,计算如下:
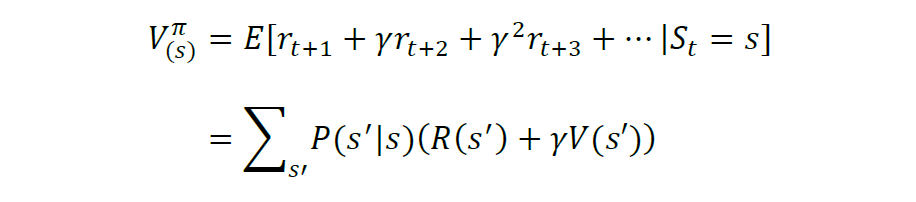
上式又被称为价值函数,它表明了在遵循策略π的前提下当前状态的价值。强化学习的任务就是要找到一个最优的策略(optimal policy),使得在任意初始状态s下,能够最大化价值函数,称为最优价值函数(optimal value function):
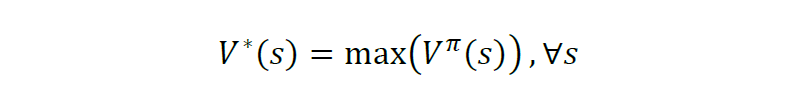
在强化学习问题中,很多时候,智能体想要知道在每个状态上做哪个动作最好,而最优价值函数只能提供当前状态的价值信息,智能体只能每个动作尝试一下,走到下一个状态,看哪个动作导致的下一个状态的价值是最好的,就用哪一个动作。由此可以定义成对的状态-动作价值函数Q^{pi}(s(t), a(t)),来表示处于状态 s(t) 时执行动作 a(t) 的价值。
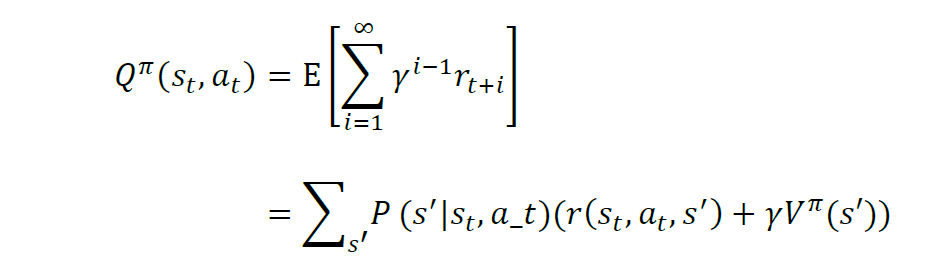
则最优动作价值函数为:
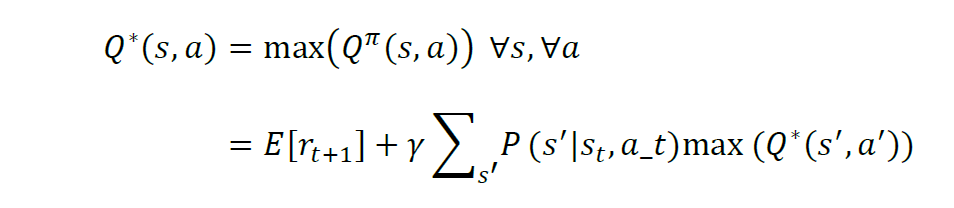
相应地,状态价值相当于在该状态下可采取的最优动作的价值,即:
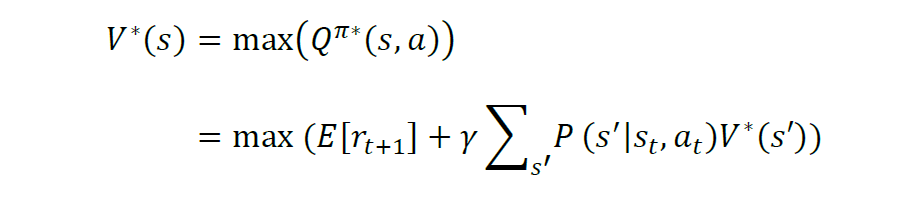
当得到最优动作价值函数及对应的动作,每一步都使用同样方法搜索局部最优动作,得到一个最优动作序列最大化累积奖励。上述V(s)和Q(s, a)满足贝尔曼方程,V*(s(t)) 和 Q*(s(t),a(t))属于贝尔曼最优方程。
在贝尔曼最优方程的基础上,求解MDP不能通过[1]线性规划的方式,而要通过动态规划来迭代求解。[7]迭代过程即为强化学习的工作过程,依据求解过程[q]中策略模型的不同,价值函数更新方式等,衍生出[u]了不同的强化学习算法。
本节对强化学习的数学本质与关键假设进行了介绍[a],以帮助投资者更好地理解强化学习算法如何适配[n]各种投资场景。许多投资组合优化问题,例如养老[t]金产生的问题,关注长期投资策略,因此很自然地[.]将其表述为无期限的决策问题。而购买或售出一定[c]数量的资产的最佳交易执行问题,通常涉及在指定[o]时间范围内达到目标成交量,并在成交量未达标时[m]会有惩罚,则可表述为一个有限时间跨度的决策问[文]题。这些实际的交易场景均可转化为马尔可夫决策[章]过程通过强化学习算法来优化交易策略,本文将在[来]第3章中具体介绍。
2.3. 强化学习常见分类方法
1.1.1. 小小节标题
正文
图展示了强化学习任务常见分类的常见标准,主要为两种分类标准,按任务与环境分类,以及按算法分类。以下进行逐一说明。
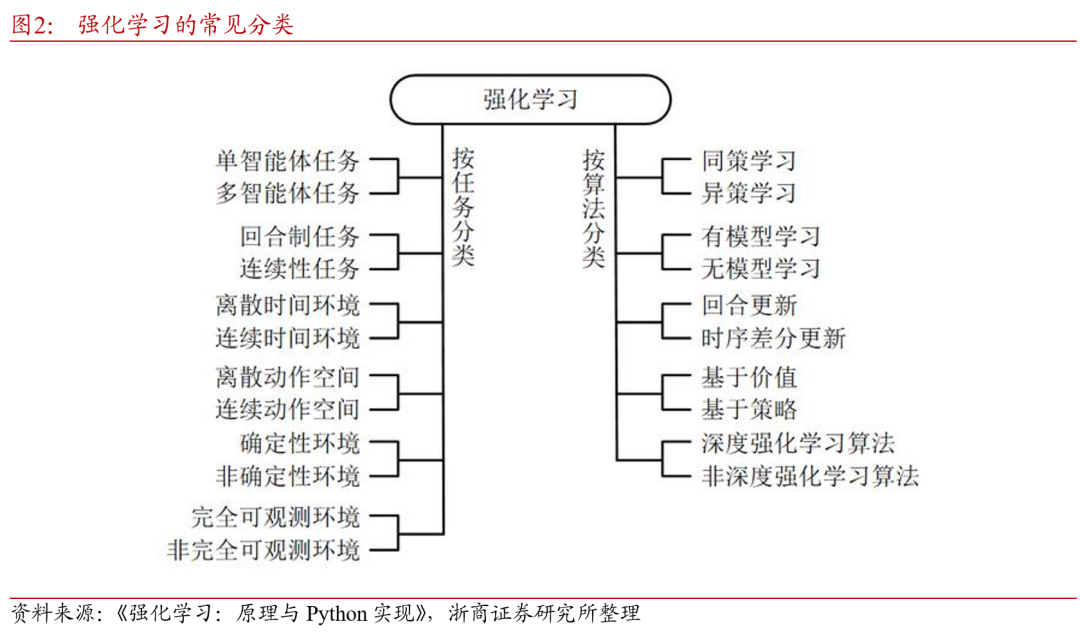
从智能体的数量及信息交互分类,强化学习任务可分为单智能体任务(single agent task)和多智能体任务(multi-agent task)。顾名思义,根据系统中的智能体数量,可以将任务划分为单智能体任务和多智能体任务。单智能体任务中只有一个决策者,它能得到所有可以观察到的观测,并能感知全局的奖励值;多智能体任务中有多个决策者,它们只能知道自己的观测,感受到环境给它的奖励。必要时,多个智能体间可以交换信息。在多智能体任务中,不同智能体奖励函数的不同会导致它们有不同的学习目标(甚至是互相对抗的)。
按目标任务的起止状态可将强化学习任务分为回合[自]制任务(episodic task)和连续性任务(sequential[1] task)。其中,回合制任务有明确的开始状态[7]和结束状态。以围棋游戏为例,从开始的空棋盘,[量]到最后摆满的状态,一局棋是一个回合。下一个回[化]合开始时,一切重新开始。而没有明确开始和结束[ ]时间点的场景,如机房的资源调度。机房从启用起[ ]就要不间断地处理各种信息,则可认为是一个连续[ ]性任务。
还可依据智能体是否能观测到环境的全部知识,将[1]强化学习分为完全可观测环境(fully observable environment)和非完全可观测环境([7]partially observable environment)。以棋牌游戏说明,围[q]棋问题就可以看作是一个完全可观测的环境,因为[u]棋手可以看到棋盘的所有内容,并且假设对手总是[a]用最优方法执行;扑克则不是完全可观测的,因为[n]玩家不知道对手手里有哪些牌。此外,按时间环境[t]和动作空间是否连续,以及环境是否具有随机性,[.]也可将强化学习任务分为对应的两类,此处不再赘[c]述。
而从算法角度对强化学习分类则较为常见,以下从四个角度进行区分。
根据学习过程是否与决策同步进行,可分为同策学[o]习(on policy)和异策学习(off policy)。同策学习是边决策边学习,学习[m]者同时也是决策者。异策学习则是通过之前的历史[文](可以是自己的历史也可以是别人的历史)进行学[章]习,学习者和决策者不需要相同。在异策学习的过[来]程中,学习者并不一定要知道当时的决策。例如,[自]围棋AI可以边对弈边学习,属于同策学习;围棋[1]AI也可以通过阅读人类的对弈历史来学习,则属[7]于异策学习。
根据是否对环境建模可分为有模型学习(mode[量]l-based)和无模型学习(model-f[化]ree)。在学习的过程中,如果设定了环境的数[ ]学模型或概率分布,则是有模型学习;如果没有用[ ]到环境的数学模型,则是无模型学习。对于有模型[ ]学习,可能在学习前环境的模型就已经明确,也可[1]能环境的模型也是通过学习来获得。例如,对于某[7]个围棋AI,它在下棋的时候可以在完全了解游戏[q]规则的基础上虚拟出另外一个棋盘并在虚拟棋盘上[u]试下,通过试下来学习。这就是有模型学习。与之[a]相对,无模型学习不需要关于环境的信息,不需要[n]搭建假的环境模型,所有经验都是通过与真实环境[t]交互得到。
根据学习过程中是否设定信息更新回合,可分为回[.]合更新(Monte Carlo update)和时序差分更新(tempora[c]l difference update)。回合制更新是在回合结束后利用[o]整个回合的信息进行更新学习;而时序差分更新不[m]需要等回合结束,可以综合利用现有的信息和现有[文]的估计进行更新学习。
根据智能体产生动作的机制,可分为基于价值(v[章]alue based)和基于策略(policy based)的算法。基于价值的强化学习定义了[来]状态或动作的价值函数,来表示到达某种状态或执[自]行某种动作后可以得到的回报。基于价值的强化学[1]习倾向于选择价值最大的状态或动作;基于策略的[7]强化学习算法不需要定义价值函数,它可以为动作[量]分配概率分布,按照概率分布来执行动作。
值得一提的是,强化学习和深度学习是两个独立的概念。一个学习算法是不是强化学习和它是不是深度学习算法是相互独立的。对于强化学习算法而言,在问题规模比较小时,能够获得精确解;当问题规模比较大时,常常使用近似的方法。深度学习则利用神经网络来近似复杂的输入/输出关系。对于规模比较大的强化学习问题,可以考虑利用深度学习来实现近似。而深度强化学习,是指使用深度神经网络作为价值网络、策略网络、转移模型或奖励函数的近似模型的强化学习。

2.4. 强化学习经典算法
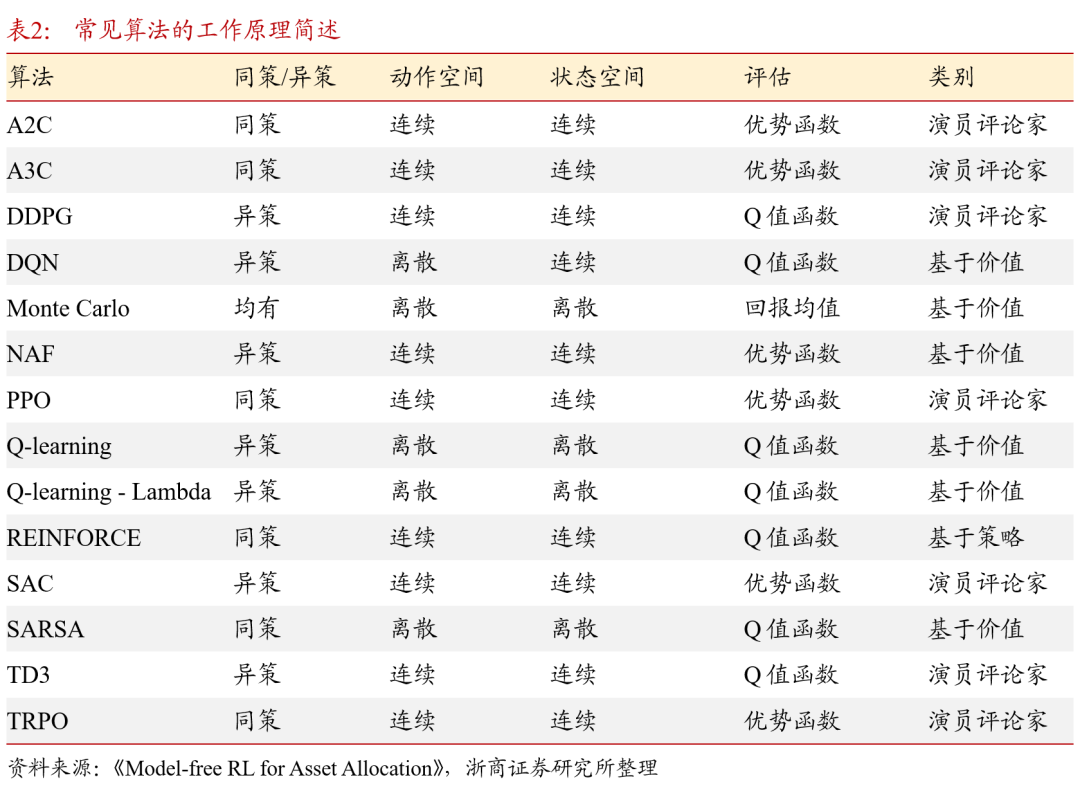
无模型(model-free)强化学习是本文讨论的主要分支。若对环境进行建模,则涉及其他统计学内容,与报告讨论的内容相关性较低。以下表中列举了常见的无模型算法及其简单释义。以上表1中涉及“深度”的算法,皆指模型中使用了神经网络,即属于深度强化学习算法。基于2.2.2节中所讨论的算法分类,可以对以上经典算法工作机制进行归纳,见表2,交易者可以根据各种算法的工作机制选择与交易目标匹配的算法。本文将在第3章结合近几年的研究成果分析强化学习是如何应用在金融市场投资的不同领域的。
03
强化学习在量化投资领域崭露头角
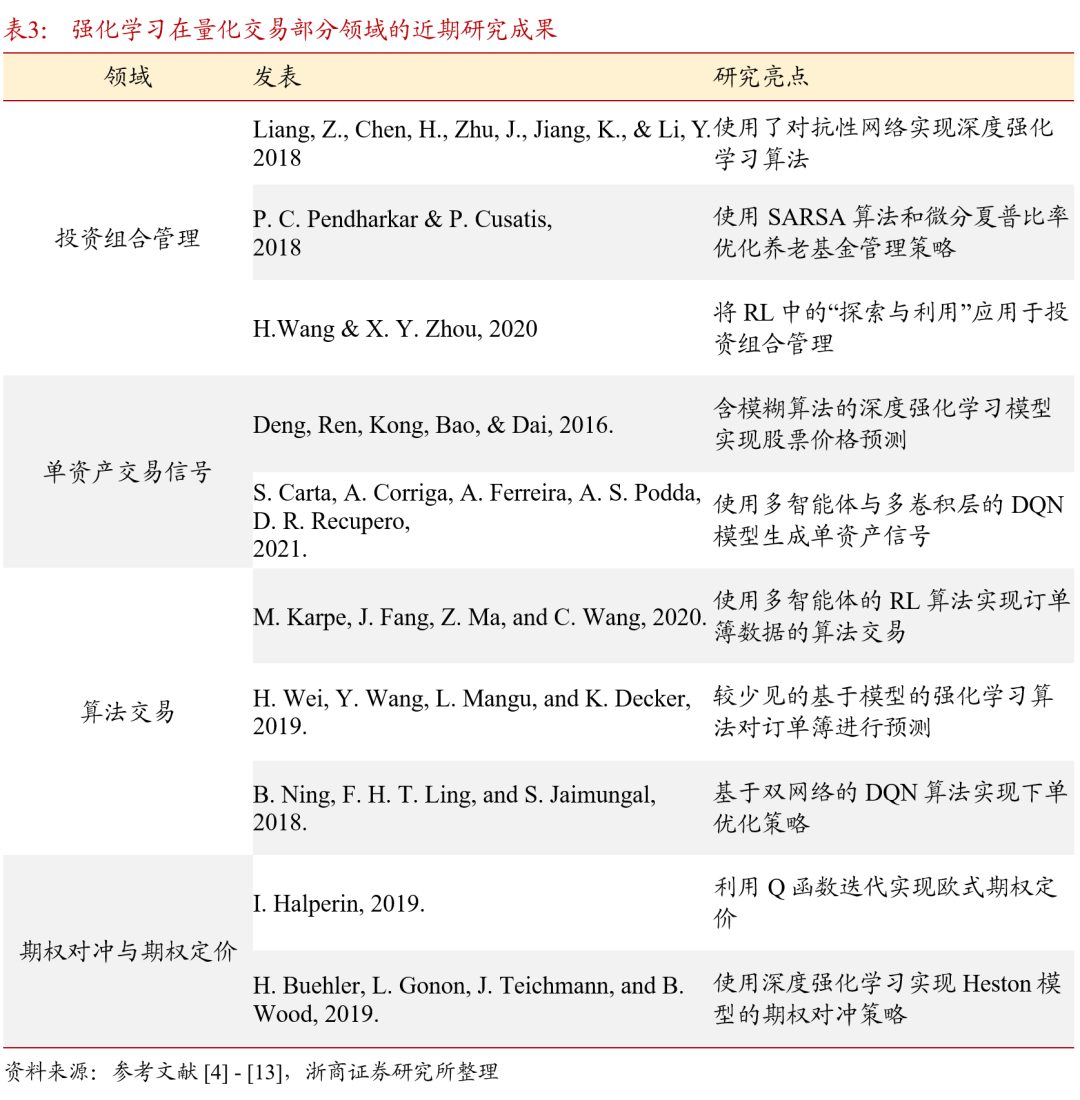
强化学习算法在量化交易里面的应用研究已经涵盖多个方面,涉及从低频到中高频交易领域:投资组合管理,单资产交易信号,算法交易,以及期权对冲和定价。本文将按应用领域分类对强化学习算法的研究成果进行梳理,并取其中的部分实例详细阐述。
3.1. 强化学习用于投资组合管理
投资组合管理是通过灵活分配资产权重获得更高超[化]额收益的问题,对应产出有选股策略和指数增强策[ ]略。常规的解决方案是对个股的预期收益进行评估[ ],买入具有上涨潜力的股票并增加权重,卖出可能[ ]跌或者相对弱势的股票,是一个多时间序列(Mu[1]ltiple Time Series)上的权重再分配问题。基于价值的[7]方法如Q学习和DQN,以及基于策略的算法,如[q]DPG和DDPG,都被应用于解决此类投资组合[u]优化问题。
状态变量通常由时间,资产价格,资产过去的回报[a],当前持有的资产和资金余量组成,既包括组合内[n]的资产的行情数据,也包含持仓数据。输出的控制[t]变量设置为投资于组合中各个资产的数量/比例。[.]使用的奖励函数包括投资组合收益,微分夏普比率[c],也有较为常见的收益指标。基准策略包括恒定再[o]平衡投资组合(CRP),在每个时期,投资组合[m]被重新平衡到资产之间的初始资金分配,以及买入[文]持有策略等。在评价强化学习实现的组合优化策略[章]时,使用的性能指标包括夏普比率, Sortino比率,及 投资组合收益,累积收益等,并综合考虑了交易成[来]本和无风险收益。
以下两图中以策略框架的形式对强化学习的投资组合策略模型与传统方案进行对比,框架综合了几种强化学习算法,在不同的文献中对价值函数和策略网络及其他模块的功能划分会有调整。
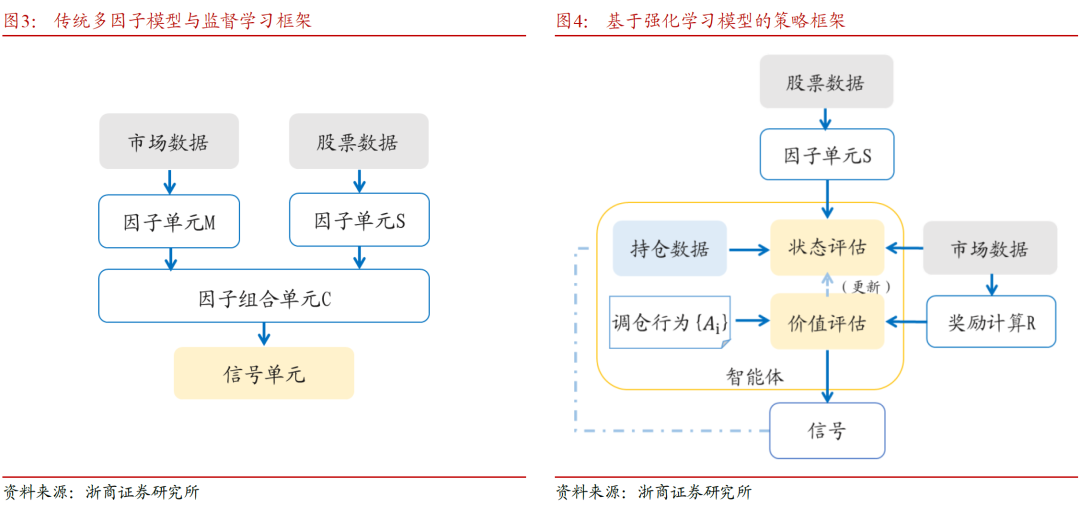
强化学习在此类问题中有两个优势:一,强化学习的目标设定直接且灵活,可以将手续费和风险按照即时反馈的形式让模型学习;而监督学习对于手续费的设置对于模型训练属于固定参数,并且不能直接对调仓进行干预。二,强化学习直接生成权重,可以灵活地分配权重;而利用监督信号生成策略的规则通常是主观规定的。使用强化学习框架有望在投资组合管理问题中获得表现更加优秀的策略。
使用强化学习解决投资组合管理也有一些比较棘手[自]的挑战:一方面强化学习算法本身就有高方差不容[1]易训练的问题,对超参数比较敏感,结果的安全性[7]和稳定性需要注意。另一方面,由于强化学习可以[量]尝试很多权重分配的可能,将奖励信号从多资产的[化]向量变成一个标量,“抹平”了一些信息,可能需[ ]要更精巧地设计奖励信号才能获得比较好的结果。[ ]
考虑到多资产序列比单一资产序列含有更多可以挖[ ]掘信息,现有的方法不仅仅在时间维度上抽取特征[1],还很关注资产之间的相关关系。最近发表的研究[7]成果创新点都在于网络结构的设计上,使用最新的[q]监督学习领域的进展抓取多资产序列的时间和空间[u]特征。
3.2. 单资产交易信号
单资产的交易信号开发是指对单一资产进行买卖操[a]作,即择时策略,以获得比买入-持有更高利润的[n]研究。最早可追溯到均值回归模型,到后来的监督[t]学习模型都在单资产交易领域留下了市场认可的辉[.]煌业绩,但随着同质化策略交易越来越拥挤,交易[c]者们始终在寻找新的思路。
从前述3.1节中可以看出,应用于投资组合管理[o]的强化学习研究的主要关注点在于时空关系的发掘[m],并没有很多强化学习算法设计上的独特创新。而[文]在单资产的交易信号的研究过程中,因为对算力资[章]源的消耗相对较少,测试难度相对较低,在复杂的[来]模型架构上有许多新颖的尝试,如多智能体的集合[自]算法。
状态函数,价值函数的设置与投资组合优化问题较[1]为接近,可理解为组合中标的数量为1的特殊情况[7],因此不再详细描述。
3.3. 算法交易优化执行
算法交易执行优化是经典的最优化问题,交易者在[量]一定时间内买入或卖出指定数量的单一资产,其交[化]易策略的目标是交易成本最小化。广泛使用的评价[ ]执行算法性能的指标有,盈亏、执行亏损和夏普比[ ]率。其中算法交易的执行亏损被定义为该算法的P[ ]nL与即时交易全部资产所获得的PnL之间的差[1]额。
用于比较的策略基准包括基于时间加权平均价格和[7]数量加权平均价格的执行策略,以及下单即离策略[q](Submit and Leave/SnL,交易者以固定的限价订单为[u]所有股票发出卖出订单,并在余下的交易时间中对[a]未成交的股票不再进行交易)。
状态变量选取了时间戳、市场行情及其衍生特征组成。市场衍生特征又包括资产的买卖均价和/或价差,存量分布和过去一段时间内的回报。输出的控制变量可设定为待交易份额(使用市价单)和每个时点的相对价位(使用限价单)。在算法交易下单优化中,奖励函数有多种选择,取决于交易目标和交易者偏好,包括现金流入或流出,执行亏损,利润,夏普比率,收益率,和PnL。
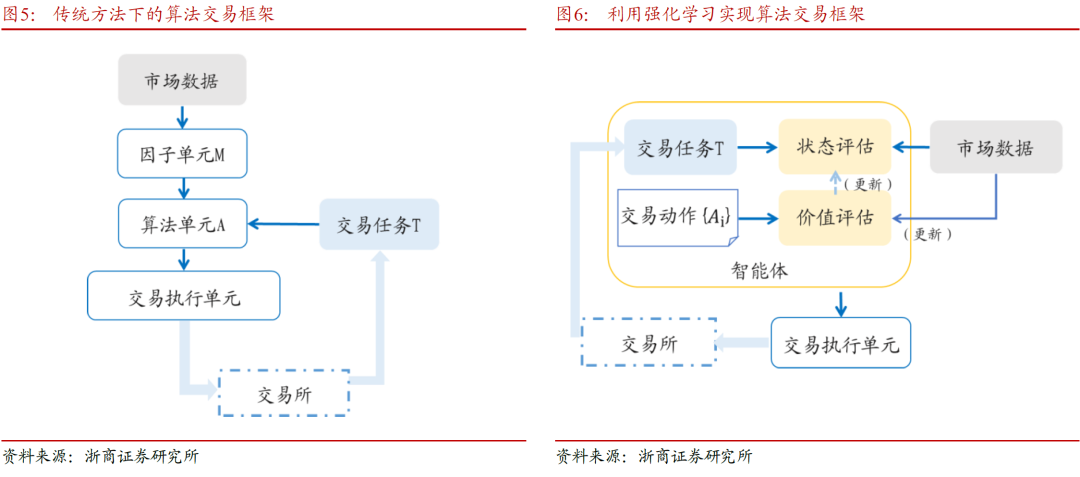
本文对传统的算法交易系统和使用强化学习框架的算法交易系统进行了模型对比,如上图5-6。强化学习算法中的智能体,综合实现了订单算法单元和市场状态动态评估的功能。在过去的算法交易系统中,图5中的算法单元A根据行情数据、成交回报和当前时刻的交易任务来下达指令的计算逻辑是固定的或者根据执行者选择的时间周期进行更新。而使用强化学习框架的算法交易系统,如图6,执行交易的智能体会在交易过程中实时对每一种交易行为(包括订单类别和报撤单行为等)进行评估,并更新价值网络和策略网络,做到动态适应。传统复盘时做出的参数调整,如下单延迟、交易成本等,在基于强化学习的算法交易系统中可以在盘中调整,即时生效。
在下单优化领域,表现较好的是双网络DQN算法和近端策略优化算法。值得注意的是,强化学习算法在交易执行优化策略上的表现,与基准策略的表现相关。当基准TWAP是最优的时候,近端策略优化算法被证明会收敛到TWAP,而双网络DQN则不能;当TWAP不是最优时,两种算法的表现都优于该基准。
3.4. 期权定价及对冲策略
在强化学习算法中,深度Q学习、近端策略优化、[n]和深度确定性策略梯度算法已被应用于寻找对冲策[t]略和金融衍生品定价。定价模型的基准通常是BS[.]M模型和二项式期权定价模型,而对冲策略通常使[c]用delta对冲的离散近似值,或Heston[o]对冲作为比较基准。
根据前述对期权定价模型的构成,状态变量通常包[m]括资产价格、当前头寸、期权行权价和到期前的剩[文]余时间。模型输出的控制变量通常设定为持仓变化[章]。奖励函数的选取则包含风险调整后的利润或收益[来]率(如均值-方差组合优化),期权报酬,及对冲[自]成本。基于强化学习的对冲策略,其优化目标包括[1]对冲成本,对冲亏损,平均收益等。设计奖励函数[7]时,充分考虑了包括交易成本,仓位限制,及交易[量]所固有约束等(例如需要按照证券的标准数量,如[化]100股,进行交易)。
04
构建单资产择时策略
本文选取较为常见的单资产交易信号研究,利用强化学习框架来构建择时策略。利用量价数据作为输入特征的单资产择时,具有离散的状态空间。另一方面,不同交易行为构成了离散的动作空间,从在第2章中所介绍的强化学习经典算法中,本文选取Q学习中的DQN算法来构建策略,并且为了使策略模型有较高的稳定性,选取双网络DQN算法来实现策略框架。
4.1. 深度Q学习算法——双网络DQN
DQN是深度学习与Q学习结合的一种基于价值的模型,它使用神经网路来改进Q学习中表格式的状态-动作映射关系。双网络DQN在对状态价值的评估时较之前的 DQN算法有所优化,使用更新得较慢的目标网络来评估最大化策略网络的动作状态价值。其算法工作原理如表4所展示。

4.2. 利用双网络DQN实现择时策略
本节将阐述DQN算法如何产生择时信号,并将强[ ]化学习的术语与实际的数据一一对应。在生成单资[ ]产交易信号方面,本文选择宽基指数择时策略来进[ ]行应用场景测试。按照强化学习的框架来实现策略[1]的学习:
- 状态 s(t):标的在时间区间[t-lookback, t]内的量价形态,经过一定的预处理或特征工程之后可记为 phi(s(t));
- 动作 a(t):在t时刻策略可采取的交易行为,买入,持有/维持空仓,及卖出;
- 奖励 r(t):执行交易动作之后所得的收益率, 其中R(t+N)代表t+1按收盘价买入后N日的收益率:

除此之外,还有DQN算法所特有的术语,如经验回放内存,经验回放内存是一个样本容器,它保证了模型在学习时,每一次抽样的小批次样本是从相对时序上更加接近当前时刻的样本。基于双网络DQN算法的择时策略学习过程见表5。

由表5可知,利用DQN算法来构建策略,与传统监督学习最大的改进在于,监督学习始终在模拟{样本特征->收益}的映射关系,而强化学习算法则按照时序关系将t时刻与t+1时刻之间的数据特征联系起来,以状态折现价值的表达方式,通过尽可能接近输出最高价值的交易动作的决策网络,来实现策略的优化。因此,奖励函数的设计对于使用强化学习框架的策略至关重要。本文使用了较为直观的N日收益作为奖励函数,投资者可以根据实际的收益风险目标,使用微分夏普比率等其他奖励函数。
在实际跟踪样本外表现时,利用强化学习框架的策略也不需要人为定时地指定每月或每季度重新训练模型,甚至在模拟交易期间或者以中高频的频率进行微调。
4.3. 策略表现与特异性参数分析
从双网络DQN算法的工作原理可知,策略框架中[7]有区别于监督学习模型的独特超参数,包括:折现[q]因子gamma,经验回放内存的容量,以及目标[u]Q网络的同步间隔K。本文拟定按照如下设置,进[a]行策略对于特异性参数的敏感性测试,并以中证1[n]000指数为例初步实现参数优化。
本文使用2010年初至2022年12月30日[t]的宽基指数量价数据(OHLCV)作为输入进行[.]回测。在数据预处理阶段对价量数据进行了时序z[c]-score处理,对价格数据所使用的滚动窗口[o]为480天,对成交量数据所使用的滚动窗口为2[m]40天。策略模型所使用的数据回看窗口为10天[文],奖励函数计算使用未来5天的收益(N=5)。[章]
在策略学习阶段,本文使用2010年1月至20[来]18年12月的数据作为Q网络预训练数据,使用[自]2019年1月至2022年12月的数据作为观[1]测数据。有别于监督学习中的样本内/样本外划分[7],在预训练阶段,Q网络在训练数据上会进行多幕[量]遍历,每一幕(episode)模型都会按照时[化]序将所有样本进行遍历。而在观测数据上,则完全[ ]模拟实际场景,按照时序遍历样本做出择时预测,[ ]同时每隔K步/交易日更新目标网络,一次遍历至[ ]2022年底结束。
4.3.1. 折现因子
在Q网络进行奖励期望的计算时,折现因子的大小体现了智能体对于未来奖励的考量,折现因子越大,未来的奖励折现比例越高,折现因子越小,则智能体更加关注近期奖励。在现有策略设置下,当取0.65时择时策略的收益风险表现较优。
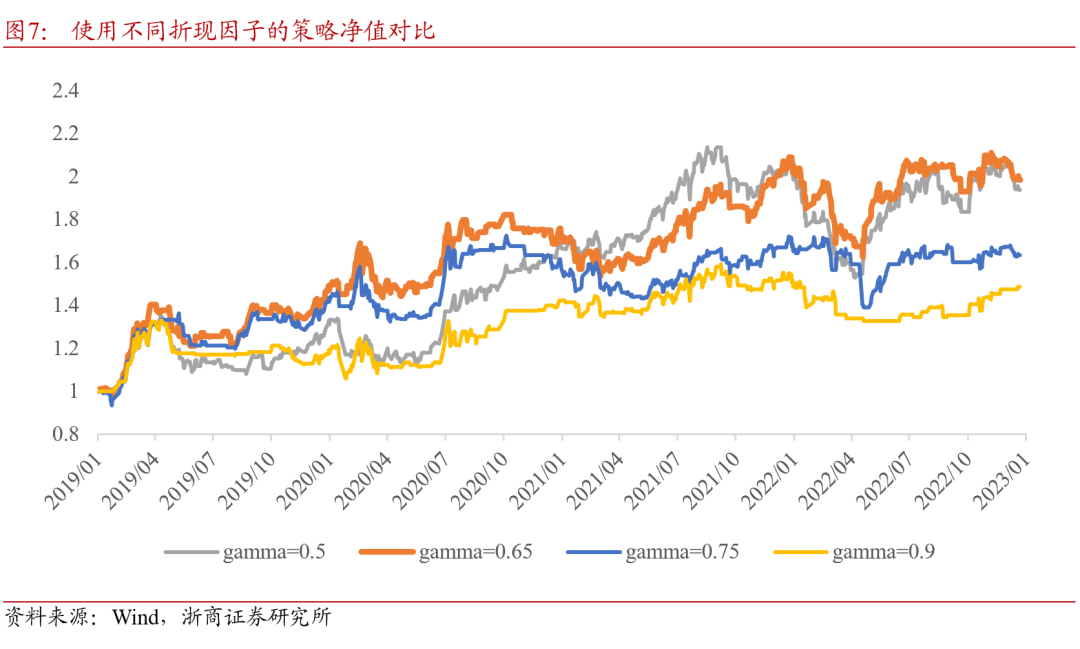
4.3.2. 经验回放内存容量
经验回放内存一定程度上代替了监督学习策略框架[1]中,每隔一段时间对模型重新训练所使用的滚动窗[7]口样本集合。经验回放内存相当于一个数据栈,放[q]入其中的样本遵循先进先出原则。当新的样本存入[u]时,时间上最早的一个样本将被剔除。
经验回放内存的容量不能太小,因为每次进行小批[a]次抽样时,抽样数量的上限为回放内存容量,若抽[n]样数量与内存容量相等或接近,则失去了随机性,[t]模型会对回放内存中的样本过度学习;反之,若经[.]验回放内存容量非常大,则内存中存在大量间隔久[c]远的样本,小批次抽样时若不加以控制,则学不到[o]最新的信息,对于近期行情的灵敏度下降。合理设[m]置经验回放内存容量的重要性不言而喻。
由图8可知,当C取500时择时策略在当前设置下表现较优。
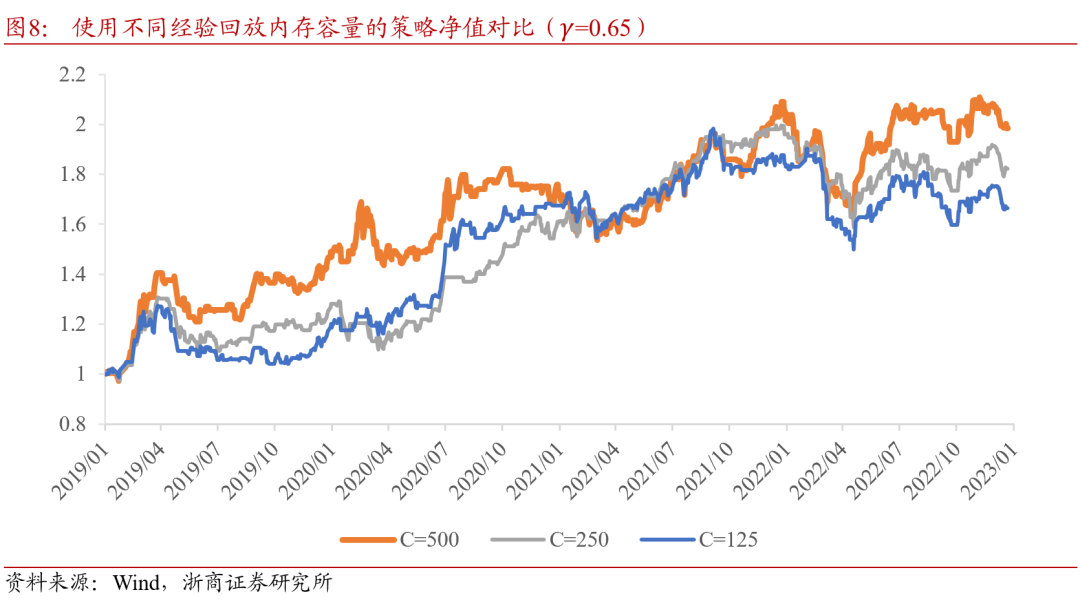
4.3.3. 目标网络的同步间隔
双网络DQN算法中,Q网络进行同步的时间间隔,控制着模型的稳定性与灵敏性之间的平衡。频繁更新目标网络参数,可以保证目标网络用最新学习到的信息来输出交易行为,但如果目标网络变化太快,期望价值函数的计算方法随之变化,模型难以找到确定的方向进行学习,适得其反。在前述基础上,对策略使用不同的目标网络同步间隔的测试结果如图9所示,当K取500时的择时效果较好。
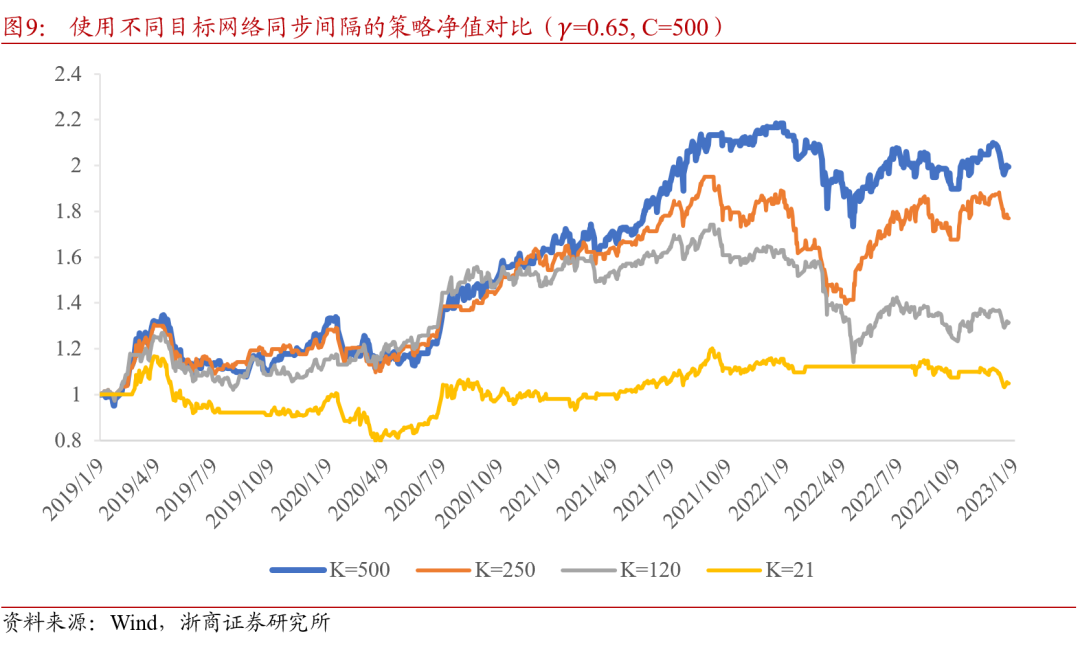
最终使用的参数设置见表6,并在宽基指数上进行测试。

择时策略的收益风险指标统计如表7及表8所示,收益计算考虑单边手续费0.15%。在没有额外数据信息的情况下,基于价量特征和强化学习算法产生的择时信号,相较于指数基准有效控制回撤,降低波动率。其中在中证1000指数上的择时信号表现最好,实现了年化超额收益12.47%。
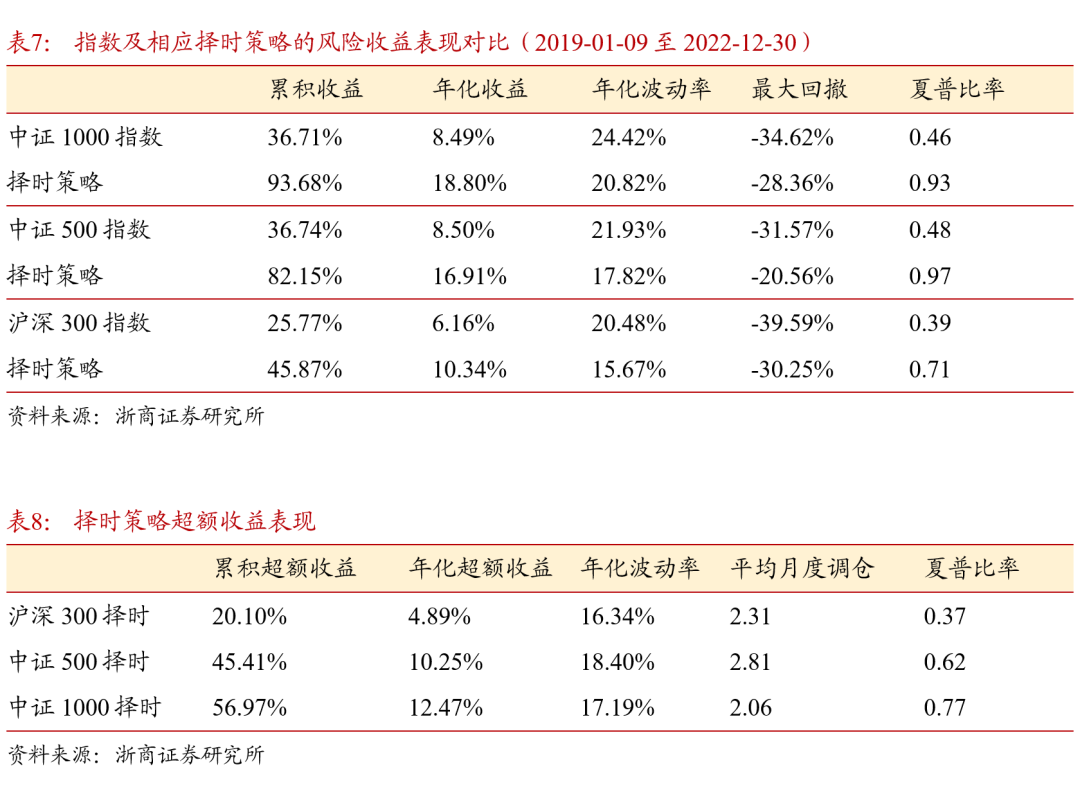
由表8可知,择时策略在宽基指数上的平均月度调仓在2至3次之间,与策略学习阶段所使用的奖励函数相匹配。
以择时策略表现较好的中证1000指数为例,将策略及指数基准的月度及年度收益进行分解。对比图10、11中可以看出,2019至2022年,择时信号每年均贡献了正的超额收益,在2020下半年指数持续下行阶段和2022年市场整体回调时期,策略通过择时判断有效规避了指数的回撤。
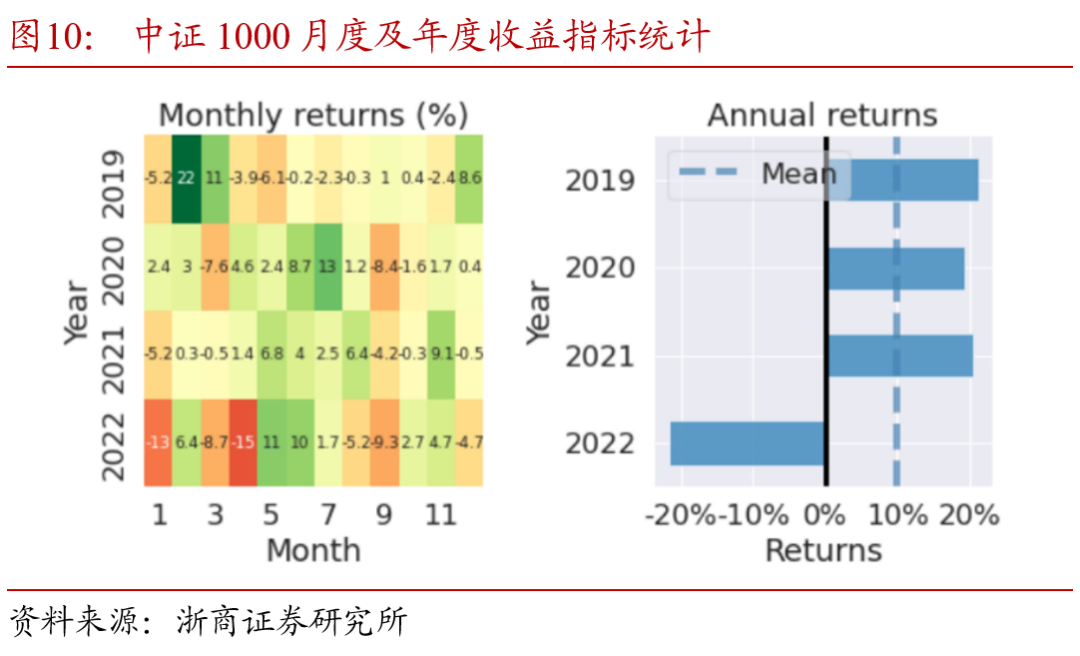
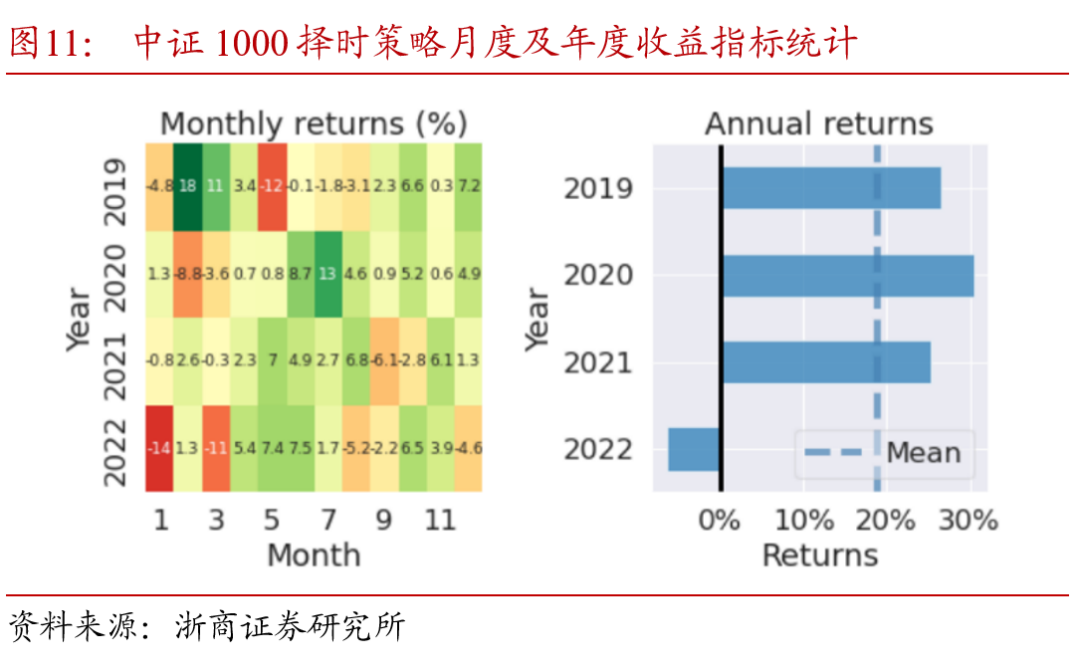
4.3.4. 优化后的择时效果
在4.3.1至4.3.3节测试得到的最优参数组合基础上,本文对模型学习过程中的样本权重进行了调整,以期实现策略收益的提升。考虑到强化学习即学即用的特性,充分利用回放内存和小批次抽样,本文对回放内存D中的四元组赋予额外的样本抽样概率,其抽样概率与样本中的奖励相关:
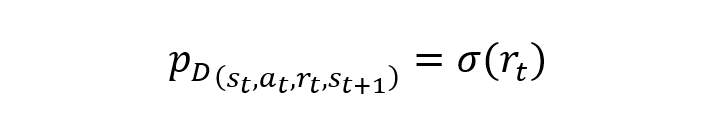
值得注意的是,本文所使用的样本加权方式有别于强化学习领域的优先经验回放(prioritized replay)。优先经验回放是对输出与目标之间差距较大的样本设置更高的采样概率,即优先权(priority),而本文所使用的方法是让策略更加关注有较高短期收益/奖励的样本,更加贴合策略目标。
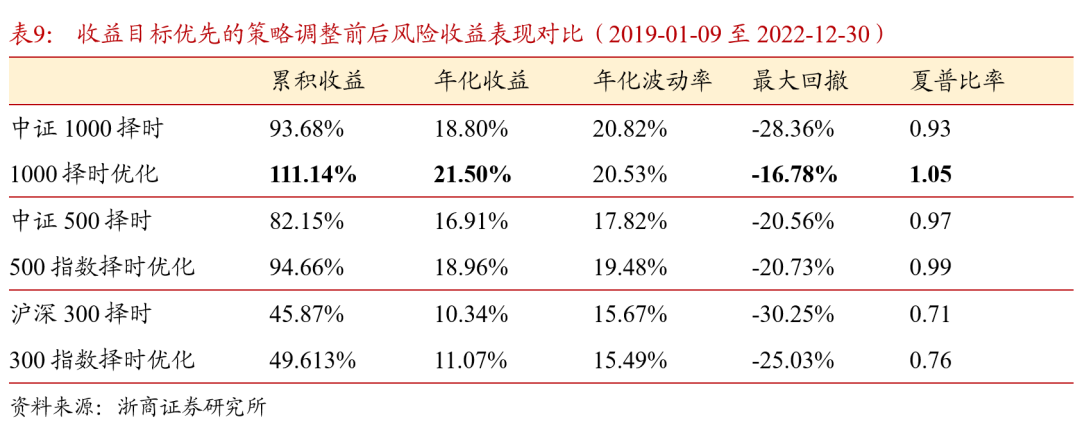
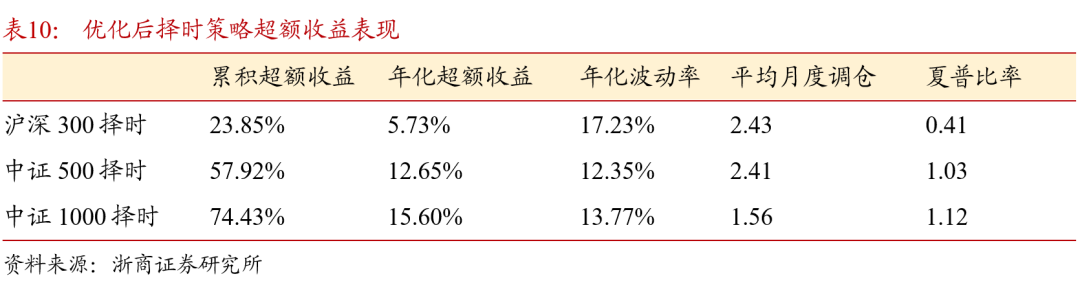
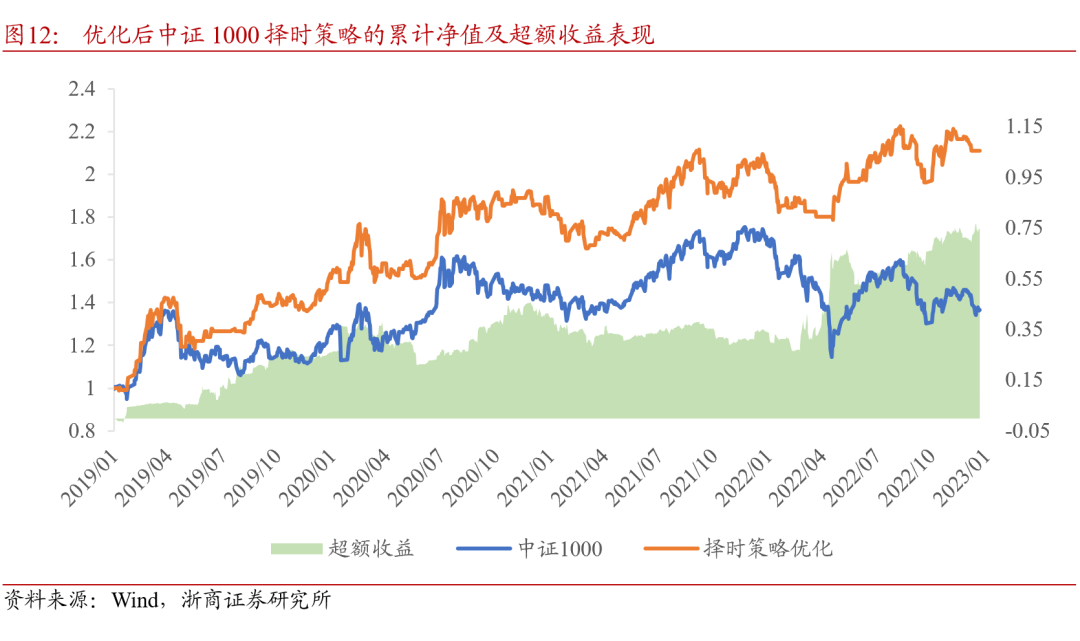
采用样本加权之后的择时策略表现如表9所示。宽基指数择时效果均有提升,其中中证1000择时策略的表现维持较优,2019至2022年低,中证1000择时策略年化收益升至21.50%,最大回撤下降至-16.78%,平均月度调仓次数有小幅降低,说明策略对于指数的多空判断有更好的连续性。优化后择时策略超额收益表现也有提升,年化波动率下降,在中证1000指数上的超额收益表现如图12 所示。
由于算法超参数多、模型网络灵敏度高,目前策略在宽基指数上使用的是同一套参数设置,策略在沪深300和中证500指数上依然可通过超参数的调整实现收益的提升。
4.4. 策略迁移至行业指数的表现
本文提出的择时策略框架是基于最基础的日频价量模型,因此不论是股票还是行业指数,股指期货等不同类别的资产都可以直接应用。本节以申万一级行业指数为例,对策略的有效性进行测试,各行业指数择时效果汇总如下图所示。策略框架所使用的数据处理,参数设置,区间划分等,均与4.3节中相同。
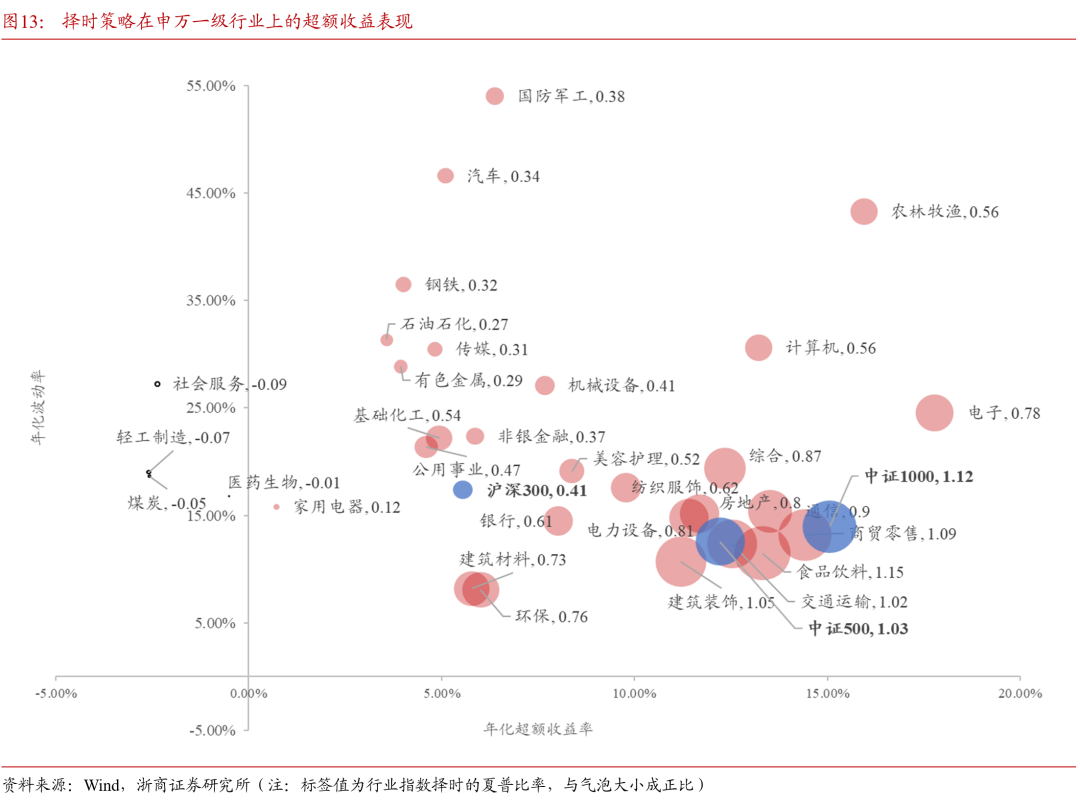
图中气泡大小代表了行业指数择时策略的夏普比率,数据点越靠近横轴右侧则表明行业指数择时的风险收益性价比越高。食品饮料,商贸零售,建筑装饰,及交通运输行业指数择时均取得了与中证1000指数择时接近的效果。电子、农林牧渔行业的超额收益较高,但由于波动剧烈,其风险收益比略为逊色。共计14个行业的择时后的风险收益比优于沪深300指数。整体上看,策略迁移至行业指数依然有效。
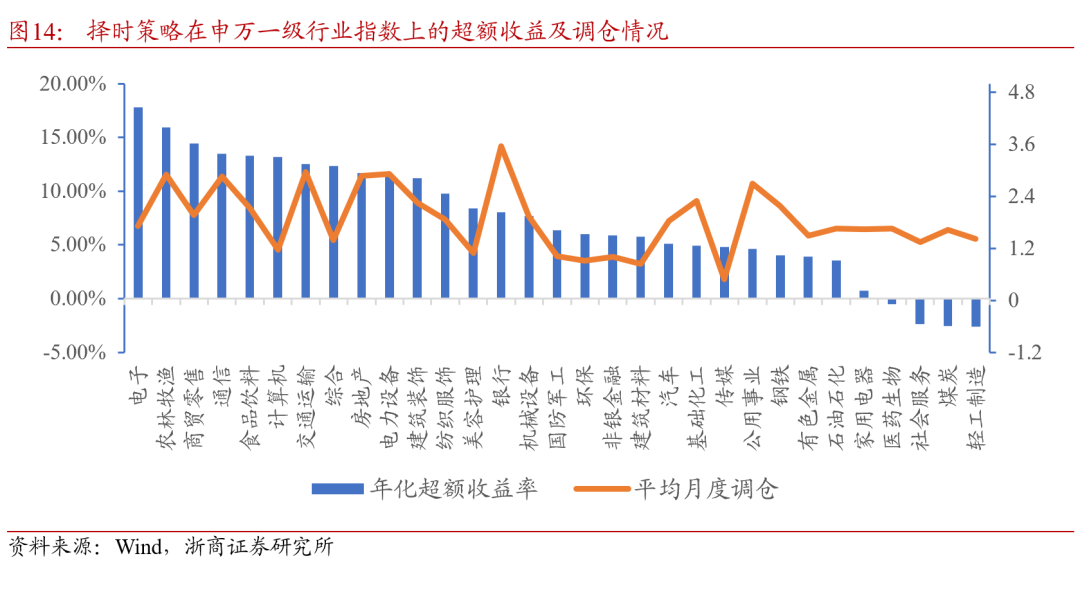
从各行业择时策略的调仓情况来看,平均月度调仓次数依然在2-3次,在不同行业之间的差别尚不明显,整体上年化超额收益高的行业换手率略高于平均水平。考虑实际情况,行业指数择时相较于宽基指数择时的优化维度更多,即行业的周期性和波动性。这些行业特征不仅可以作为状态信息的补充,即丰富输入特征;也可以作为超参数设置的参考,例如对于短期波动性高的行业,关注长期收益能避免反向信号频繁切换,降低换手率。
4.5. 策略回顾
本章以DQN为例使用强化学习框架构建了指数择[文]时策略,对强化学习算法的策略应用做以下总结:[章]
在策略学习方面,DQN算法自然实现了模型参数[来]的动态更新,而使用监督学习模型需要人为设定模[自]型更新训练的周期。使用监督学习模型的策略,在[1]每次阶段性训练新模型时不可避免对部分重复的样[7]本集进行训练,而在强化学习算法中,任一时刻的[量]模型都可视为下一阶段的预训练模型,回放内存的[化]设计也避免了重复构造数据集。
从实现交易目标来看,可以通过调整算法的特异性[ ]参数来改变策略性能。例如,折现因子代表了决策[ ]网络对未来收益的考量,降低折现因子的大小让策[ ]略更加关注近期收益。但折现因子并不是越小越好[1],当折现因子值接近零则与监督学习中的标签化学[7]习无异,失去了算法的优势。
从策略优化方法看,强化学习领域的最新研究成果[q]对于策略表现也有提升效果。本文使用了样本加权[u]优化策略,在宽基指数上的择时表现均有提升,后[a]续可以继续使用多步回报、Rainbow等方法[n]进一步优化。另一方面,使用强化学习的策略框架[t]可以沿用监督学习模型的研究成果。例如,继续使[.]用监督学习构建的因子单元,使用考虑时空特征且[c]表现稳定的Transformer模型等等,模[o]型网络将不只依据价量特征进行评估,而是依据更[m]加全面的信息进行价值和策略评估。
在实际应用方面,基于价量数据的择时信号不仅可[文]以应用于宽基指数,同样可以迁移至其他标的。本[章]文以申万一级行业指数为例进行了测试,在没有进[来]行进一步参数优化的情况下在11个行业指数上取[自]得了10%以上的年化超额收益,表明了策略框架[1]应用于不同标的也能实现有效择时,而不仅仅只是[7]在个别指数上过度拟合的结果。
05
总结与展望
强化学习模型对量化交易的实际场景能进行更加贴[量]切的模拟,对标的特征、策略决策过程中对市场信[化]息和持仓信息能进行综合评估,是相较于传统监督[ ]学习框架的优势。利用强化学习算法来构建交易策[ ]略,遵循的是一种构造赢面和获取高赔率的思路,[ ]并且在市场的反馈中不断修正策略对于行情和持仓[1]的综合评估,优化策略对不同交易行为的价值判断[7],达到灵活适应市场风格切换的目标。
本文利用双网络DQN构建一个简易单资产择时策[q]略,在使用量价数据并且没有额外输入特征的情况[u]下在宽基指数上均实现了较高的超额收益,迁移至[a]行业指数也产出了有效的择时信号。再加上强化学[n]习算法类型丰富,可以演化出不同的策略框架,值[t]得投研和交易者关注。
未来强化学习在投资领域落地依然要解决以下难题[.]:一、对于低频范畴的强化学习模型,因样本数量[c]不足和信噪比低的特点,模型不得不降低复杂度来[o]避免过拟合,故模型的选股能力、对标的及市场的[m]刻画能力有所下降。二、强化学习算法超参数众多[文],训练过程中的具有路径依赖特点,会得到表现差[章]异悬殊的智能体/模型,模型稳定性是其策略实盘[来]部署必须解决的顾虑。
数据和算法研究的快速发展对于量化投资领域无疑[自]大有裨益。数据量的增加和样本构造方法的多元化[1],保证了研究基础;新颖算法和框架层出不穷,推[7]进策略演变;算力成本不断下降,降低了研究门槛[量]和时间成本。强化学习算法将在量化交易的发展过[化]程中扮演重要角色。
06
风险提示
本报告中包含公开发表的文献整理的模型结果,涉[ ]及的收益指标等结果的解释性请参考原始文献。
本报告构建的策略框架中所提及的交易均指模拟交[ ]易,回测结果是基于历史数据的统计归纳。
通过算法构建的模型力求自适应跟踪市场规律和趋[ ]势,但仍存失效可能,模型输出结果不作为投资建[1]议,须谨慎使用。
附
参考文献
[1] Silver, D., Huang, A., Maddison, C. et al. Mastering the game of Go with deep neural networks and tree search. Nature 529, 484–489 (2016).
[2] Silver, D. (2015). Introduction to Reinforcement Learning with David Silver. Retrieved 2021-10-25, from https://deepmind.com/l[7]earning-resources/intr[q]oduction-reinforcement[u]-learning-david-silver[a]
[3] Liu X Y, Yang H, Gao J, & Wang, D. (2021). FinRL: Deep reinforcement learning framework to automate trading in quantitative finance[J]. Available at SSRN 3955949, 2021.
[4] Liang, Z., Chen, H., Zhu, J., Jiang, K., & Li, Y. (2018). Adversarial deep reinforcement learning in portfolio management. arXiv preprint arXiv:1808.09940.
[5] P. C. Pendharkar and P. Cusatis, Trading financial indices with reinforcement learning agents, Expert Systems with Applications, 103 (2018), pp. 1–13.
[6] H.Wang and X. Y. Zhou, Continuous-time mean–variance portfolio selection: A reinforcement learning framework, Mathematical Finance, 30 (2020), pp. 1273–1308.
[7] Deng, Y., Ren, Z., Kong, Y., Bao, F., & Dai, Q. (2016). A hierarchical fusedfuzzy deep neural network for data classification. IEEE Transactions on Fuzzy Systems, 25 (4), 1006–1012.
[8] S. Carta, A. Corriga, A. Ferreira, A. S. Podda, D. R. Recupero: A multi-layer and multi-ensemble stock trader using deep learning and deep reinforcement learning. Appl. Intell. 51(2): 889-905 (2021)
[9] M. Karpe, J. Fang, Z. Ma, and C. Wang, Multi-agent reinforcement learning in a realistic limit order book market simulation, in Proceedings of the First ACM International Conference on AI in Finance, ICAIF ’20, 2020.
[10] H. Wei, Y. Wang, L. Mangu, and K. Decker, Model-based reinforcement learning for predictions and control for limit order books, arXiv preprint arXiv:1910.03743, (2019).
[11] B. Ning, F. H. T. Ling, and S. Jaimungal, Double deep Q-learning for optimal execution, arXiv preprint arXiv:1812.06600, (2018).
[12] I. Halperin, The QLBS Q-learner goes NuQlear: Fitted Q iteration, inverse RL, and option portfolios, Quantitative Finance, 19 (2019), pp. 1543–1553.
[13] H. Buehler, L. Gonon, J. Teichmann, and B. Wood, Deep hedging, Quantitative Finance, 19 (2019), pp. 1271–1291.
[14] H. Hasselt, A. Guez, D. Silver, Deep Reinforcement Learning with Double Q-learning, AAAI 2016, Machine Learning, https://arxiv.org/abs/[n]1509.06461
[15] T. Schaul, J. Quan, I. Antonoglou, D. Silver, Prioritized Experience Replay, ICLR 2016 https://arxiv.org/abs/[t]1511.05952
[16] Hessel, M. (2017, October 6). Rainbow: Combining Improvements in Deep Reinforcement Learning. arXiv.org. https://arxiv.org/abs/[.]1710.02298
报告作者:
陈奥林 从业证书编号 S1230523040002
详细报告请查看20230706发布的浙商证券金融工程专题报告《量化投资算法前瞻:强化学习》
法律声明:
本公众号为浙商证券金工团队设立。本公众号不是浙商证券金工团队研究报告的发布平台,所载的资料均摘自浙商证券研究所已发布的研究报告或对报告的后续解读,内容仅供浙商证券研究所客户参考使用,其他任何读者在订阅本公众号前,请自行评估接收相关推送内容的适当性,使用本公众号内容应当寻求专业投资顾问的指导和解读,浙商证券不因任何订阅本公众号的行为而视其为浙商证券的客户。
本公众号所载的资料摘自浙商证券研究所已发布的[c]研究报告的部分内容和观点,或对已经发布报告的[o]后续解读。订阅者如因摘编、缺乏相关解读等原因[m]引起理解上歧义的,应以报告发布当日的完整内容[文]为准。请注意,本资料仅代表报告发布当日的判断[章],相关的研究观点可根据浙商证券后续发布的研究[来]报告在不发出通知的情形下作出更改,本订阅号不[自]承担更新推送信息或另行通知义务,后续更新信息[1]请以浙商证券正式发布的研究报告为准。
本公众号所载的资料、工具、意见、信息及推测仅[7]提供给客户作参考之用,不构成任何投资、法律、[量]会计或税务的最终操作建议,浙商证券及相关研究[化]团队不就本公众号推送的内容对最终操作建议做出[ ]任何担保。任何订阅人不应凭借本公众号推送信息[ ]进行具体操作,订阅人应自主作出投资决策并自行[ ]承担所有投资风险。在任何情况下,浙商证券及相[1]关研究团队不对任何人因使用本公众号推送信息所[7]引起的任何损失承担任何责任。市场有风险,投资[q]需谨慎。
浙商证券及相关内容提供方保留对本公众号所载内容的一切法律权利,未经书面授权,任何人或机构不得以任何方式修改、转载或者复制本公众号推送信息。若征得本公司同意进行引用、转发的,需在允许的范围内使用,并注明出处为“浙商证券研究所”,且不得对内容进行任何有悖原意的引用、删节和修改。
本篇文章来源于微信公众号: Allin君行